This document describes the steps to construct a LL(1) predictive parsing table. It begins with a grammar and removes left recursion. It then computes the FIRST and FOLLOW sets for each nonterminal. Using these sets, it constructs the predictive parsing table by filling in the entries based on the FIRST of the right side and FOLLOW of the left side nonterminals. The table allows LL(1) parsing by predicting the next move based on the lookahead symbol.

1. Example-3: LL(1) parsing
EE+T | T
TT*F | F
F(E) | id
Step 1: Remove left recursion
ETE’
E’+TE’ | ϵ
TFT’
T’*FT’ | ϵ
F(E) | id

2. Example-3: LL(1) parsing
Step 2: Compute FIRST
First(E)
ETE’
First(T)
TFT’
First(F)
F(E) Fid
ETE’
E’+TE’ | ϵ
TFT’
T’*FT’ | ϵ
F(E) | id
E  T E’
A  Y1 Y2
Rule 3
First(A)=First(Y1)
T  F T’
A  Y1 Y2
Rule 3
First(A)=First(Y1)
FIRST(E)=FIRST(T)
FIRST(T)=FIRST(F)
F  ( E )
A  𝛼
F  id
A  𝛼
Rule 1
add 𝛼 to 𝐹𝐼𝑅𝑆𝑇(𝐴)
Rule 1
add 𝛼 to 𝐹𝐼𝑅𝑆𝑇(𝐴)
FIRST(F)={ ( , id }
NT First
E { (,id }
E’
T { (,id }
T’
F { (,id }
= {(, id }
= {(, id }

3. Example-3: LL(1) parsing
Step 2: Compute FIRST
First(E’)
E’+TE’
E’𝜖
A  𝛼
E’  𝜖
A  𝜖
Rule 1
add 𝛼 to 𝐹𝐼𝑅𝑆𝑇(𝐴)
Rule 2
add 𝜖 to 𝐹𝐼𝑅𝑆𝑇(𝐴)
FIRST(E’)={ + , 𝜖 }
E’  + T E’
NT First
E { (,id }
E’ { +, 𝜖 }
T { (,id }
T’
F { (,id }
ETE’
E’+TE’ | ϵ
TFT’
T’*FT’ | ϵ
F(E) | id

4. Example-3: LL(1) parsing
Step 2: Compute FIRST
First(T’)
T’*FT’
T’𝜖
A  𝛼
T’  𝜖
A  𝜖
Rule 1
add 𝛼 to 𝐹𝐼𝑅𝑆𝑇(𝐴)
Rule 2
add 𝜖 to 𝐹𝐼𝑅𝑆𝑇(𝐴)
FIRST(T’)={ * , 𝜖 }
T’  * F T’
NT First
E { (,id }
E’ { +, 𝜖 }
T { (,id }
T’ { *, 𝜖 }
F { (,id }
ETE’
E’+TE’ | ϵ
TFT’
T’*FT’ | ϵ
F(E) | id

5. Example-3: LL(1) parsing
Step 2: Compute FOLLOW
FOLLOW(E)
F(E) NT First Follow
E { (,id } { $,) }
E’ { +, 𝜖 }
T { (,id }
T’ { *, 𝜖 }
F { (,id }
Rule 1: Place $ in FOLLOW(E)
FOLLOW(E)={ $,
F  ( E )
A  𝛂 B 𝛃
Rule 2
) }
ETE’
E’+TE’ | ϵ
TFT’
T’*FT’ | ϵ
F(E) | id

6. Example-3: LL(1) parsing
Step 2: Compute FOLLOW
FOLLOW(E’)
ETE’
E’+TE’
NT First Follow
E { (,id } { $,) }
E’ { +, 𝜖 } { $,) }
T { (,id }
T’ { *, 𝜖 }
F { (,id }
FOLLOW(E’)={ $,)
E  T E’
A  𝛂 B
Rule 3
E’  +T E’
A  𝛂 B
Rule 3
ETE’
E’+TE’ | ϵ
TFT’
T’*FT’ | ϵ
F(E) | id
}

7. Example-3: LL(1) parsing
Step 2: Compute FOLLOW
FOLLOW(T)
ETE’
NT First Follow
E { (,id } { $,) }
E’ { +, 𝜖 } { $,) }
T { (,id }
T’ { *, 𝜖 }
F { (,id }
FOLLOW(T)={ +,
E  T E’
A  𝛼 B 𝛃
$, )
E  T E’
A  𝛼 B 𝛃
Rule 3
Rule 2
ETE’
E’+TE’ | ϵ
TFT’
T’*FT’ | ϵ
F(E) | id

8. Example-3: LL(1) parsing
Step 2: Compute FOLLOW
FOLLOW(T)
E’+TE’
NT First Follow
E { (,id } { $,) }
E’ { +, 𝜖 } { $,) }
T { (,id } { +,$,) }
T’ { *, 𝜖 }
F { (,id }
FOLLOW(T)={ +,
E’  + T E’
A  𝛂 B 𝛃
$, )
Rule 3
Rule 2
E’  + T E’
A  𝛂 B 𝛃
ETE’
E’+TE’ | ϵ
TFT’
T’*FT’ | ϵ
F(E) | id
}

9. Example-3: LL(1) parsing
Step 2: Compute FOLLOW
FOLLOW(T’)
TFT’
T’*FT’
NT First Follow
E { (,id } { $,) }
E’ { +, 𝜖 } { $,) }
T { (,id } { +,$,) }
T’ { *, 𝜖 } { +,$,) }
F { (,id }
FOLLOW(T’)={+ $,)
T  F T’
A  𝛂 B
Rule 3
T’  *F T’
A  𝛂 B
Rule 3
ETE’
E’+TE’ | ϵ
TFT’
T’*FT’ | ϵ
F(E) | id
}

10. Example-3: LL(1) parsing
Step 2: Compute FOLLOW
FOLLOW(F)
TFT’
NT First Follow
E { (,id } { $,) }
E’ { +, 𝜖 } { $,) }
T { (,id } { +,$,) }
T’ { *, 𝜖 } { +,$,) }
F { (,id }
FOLLOW(F)={ *,
T  F T’
A  𝛂 B 𝛃
+ ,$ , )
T  F T’
A  𝛂 B 𝛃
Rule 3
Rule 2
ETE’
E’+TE’ | ϵ
TFT’
T’*FT’ | ϵ
F(E) | id

11. Example-3: LL(1) parsing
Step 2: Compute FOLLOW
FOLLOW(F)
T’*FT’
NT First Follow
E { (,id } { $,) }
E’ { +, 𝜖 } { $,) }
T { (,id } { +,$,) }
T’ { *, 𝜖 } { +,$,) }
F { (,id } {*,+,$,)}
FOLLOW(F)={ *,+,
T’  * F T’
A  𝛂 B 𝛃
$, )
Rule 3
Rule 2
T’  * F T’
A  𝛂 B 𝛃
ETE’
E’+TE’ | ϵ
TFT’
T’*FT’ | ϵ
F(E) | id
}

12. Example-3: LL(1) parsing
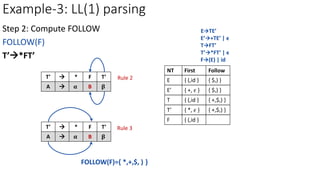
Step 3: Construct predictive parsing table
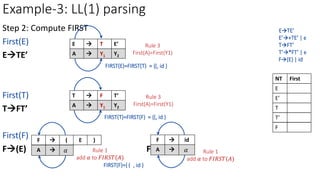
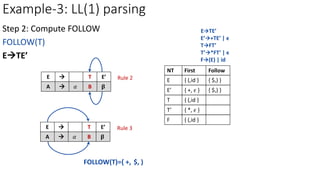
ETE’
a=FIRST(TE’)={ (,id }
M[E,(]=ETE’
M[E,id]=ETE’
NT First Follow
E { (,id } { $,) }
E’ { +, 𝜖 } { $,) }
T { (,id } { +,$,) }
T’ { *, 𝜖 } { +,$,) }
F { (,id } {*,+,$,)}
Rule: 2
A 𝛼
a = first(𝛼)
M[A,a] = A 𝛼
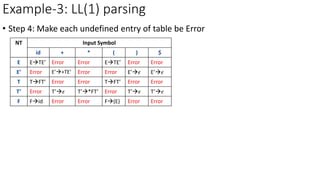
NT Input Symbol
id + * ( ) $
E ETE’ ETE’
E’
T
T’
F
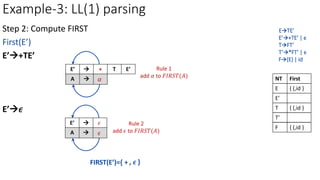
ETE’
E’+TE’ | ϵ
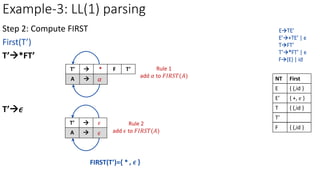
TFT’
T’*FT’ | ϵ
F(E) | id

13. Example-3: LL(1) parsing
Step 3: Construct predictive parsing table
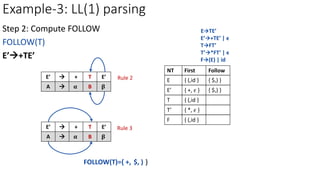
E’+TE’
a=FIRST(+TE’)={ + }
M[E’,+]=E’+TE’
NT Input Symbol
id + * ( ) $
E ETE’ ETE’
E’ E’+TE’
T
T’
F
Rule: 2
A 𝛼
a = first(𝛼)
M[A,a] = A 𝛼
NT First Follow
E { (,id } { $,) }
E’ { +, 𝜖 } { $,) }
T { (,id } { +,$,) }
T’ { *, 𝜖 } { +,$,) }
F { (,id } {*,+,$,)}
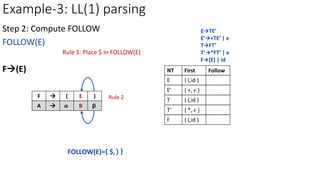
ETE’
E’+TE’ | ϵ
TFT’
T’*FT’ | ϵ
F(E) | id

14. Example-3: LL(1) parsing
Step 3: Construct predictive parsing table
E’𝜖
b=FOLLOW(E’)={ $,) }
M[E’,$]=E’𝜖
M[E’,)]=E’𝜖
NT Input Symbol
id + * ( ) $
E ETE’ ETE’
E’ E’+TE’ E’𝜖 E’𝜖
T
T’
F
Rule: 3
A 𝛼
b = follow(A)
M[A,b] = A 𝛼
NT First Follow
E { (,id } { $,) }
E’ { +, 𝜖 } { $,) }
T { (,id } { +,$,) }
T’ { *, 𝜖 } { +,$,) }
F { (,id } {*,+,$,)}
ETE’
E’+TE’ | ϵ
TFT’
T’*FT’ | ϵ
F(E) | id

15. Example-3: LL(1) parsing
Step 3: Construct predictive parsing table
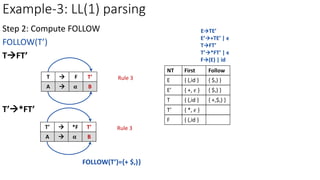
TFT’
a=FIRST(FT’)={ (,id }
M[T,(]=TFT’
M[T,id]=TFT’
NT Input Symbol
id + * ( ) $
E ETE’ ETE’
E’ E’+TE’ E’𝜖 E’𝜖
T TFT’ TFT’
T’
F
NT First Follow
E { (,id } { $,) }
E’ { +, 𝜖 } { $,) }
T { (,id } { +,$,) }
T’ { *, 𝜖 } { +,$,) }
F { (,id } {*,+,$,)}
ETE’
E’+TE’ | ϵ
TFT’
T’*FT’ | ϵ
F(E) | id
Rule: 2
A 𝛼
a = first(𝛼)
M[A,a] = A 𝛼

16. Example-3: LL(1) parsing
Step 3: Construct predictive parsing table
T’*FT’
a=FIRST(*FT’)={ * }
M[T’,*]=T’*FT’
NT Input Symbol
id + * ( ) $
E ETE’ ETE’
E’ E’+TE’ E’𝜖 E’𝜖
T TFT’ TFT’
T’ T’*FT’
F
Rule: 2
A 𝛼
a = first(𝛼)
M[A,a] = A 𝛼
NT First Follow
E { (,id } { $,) }
E’ { +, 𝜖 } { $,) }
T { (,id } { +,$,) }
T’ { *, 𝜖 } { +,$,) }
F { (,id } {*,+,$,)}
ETE’
E’+TE’ | ϵ
TFT’
T’*FT’ | ϵ
F(E) | id

17. Example-3: LL(1) parsing
Step 3: Construct predictive parsing table
T’𝜖
b=FOLLOW(T’)={ +,$,) }
M[T’,+]=T’𝜖
M[T’,$]=T’𝜖
M[T’,)]=T’𝜖
NT Input Symbol
id + * ( ) $
E ETE’ ETE’
E’ E’+TE’ E’𝜖 E’𝜖
T TFT’ TFT’
T’ T’𝜖 T’*FT’ T’𝜖 T’𝜖
F
Rule: 3
A 𝛼
b = follow(A)
M[A,b] = A 𝛼
NT First Follow
E { (,id } { $,) }
E’ { +, 𝜖 } { $,) }
T { (,id } { +,$,) }
T’ { *, 𝜖 } { +,$,) }
F { (,id } {*,+,$,)}
ETE’
E’+TE’ | ϵ
TFT’
T’*FT’ | ϵ
F(E) | id

18. Example-3: LL(1) parsing
Step 3: Construct predictive parsing table
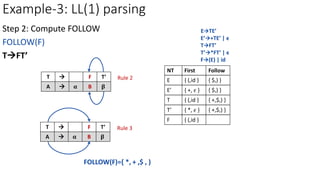
F(E)
a=FIRST((E))={ ( }
M[F,(]=F(E)
NT Input Symbol
id + * ( ) $
E ETE’ ETE’
E’ E’+TE’ E’𝜖 E’𝜖
T TFT’ TFT’
T’ T’𝜖 T’*FT’ T’𝜖 T’𝜖
F F(E)
Rule: 2
A 𝛼
a = first(𝛼)
M[A,a] = A 𝛼
NT First Follow
E { (,id } { $,) }
E’ { +, 𝜖 } { $,) }
T { (,id } { +,$,) }
T’ { *, 𝜖 } { +,$,) }
F { (,id } {*,+,$,)}
ETE’
E’+TE’ | ϵ
TFT’
T’*FT’ | ϵ
F(E) | id

19. Example-3: LL(1) parsing
Step 3: Construct predictive parsing table
Fid
a=FIRST(id)={ id }
M[F,id]=Fid
NT Input Symbol
id + * ( ) $
E ETE’ ETE’
E’ E’+TE’ E’𝜖 E’𝜖
T TFT’ TFT’
T’ T’𝜖 T’*FT’ T’𝜖 T’𝜖
F Fid F(E)
Rule: 2
A 𝛼
a = first(𝛼)
M[A,a] = A 𝛼
NT First Follow
E { (,id } { $,) }
E’ { +, 𝜖 } { $,) }
T { (,id } { +,$,) }
T’ { *, 𝜖 } { +,$,) }
F { (,id } {*,+,$,)}
ETE’
E’+TE’ | ϵ
TFT’
T’*FT’ | ϵ
F(E) | id

20. Example-3: LL(1) parsing
• Step 4: Make each undefined entry of table be Error
NT Input Symbol
id + * ( ) $
E ETE’ Error Error ETE’ Error Error
E’ Error E’+TE’ Error Error E’𝜖 E’𝜖
T TFT’ Error Error TFT’ Error Error
T’ Error T’𝜖 T’*FT’ Error T’𝜖 T’𝜖
F Fid Error Error F(E) Error Error

21. Example-3: LL(1) parsing
Step 4: Parse the string : id + id * id $
STACK INPUT OUTPUT
E$ id+id*id$
TE’$ id+id*id$ ETE’
FT’E’$ id+id*id$ TFT’
idT’E’$ id+id*id$ Fid
T’E’$ +id*id$
+TE’$ +id*id$ E’+TE’
E’$ +id*id$ T’𝜖
idT’E’$ id$ Fid
TE’$ id*id$
T’E’$ $
FT’E’$ id*id$ TFT’
E’$ $ T’𝜖
FT’E’$ id$
$ $ E’𝜖
*FT’E’$ *id$ T*FT’
T’E’$ *id$
idT’E’$ id*id$ Fid
NT Input Symbol
id + * ( ) $
E ETE’ Error Error ETE’ Error Error
E’ Error E’+TE’ Error Error E’𝜖 E’𝜖
T TFT’ Error Error TFT’ Error Error
T’ Error T’𝜖 T’*FT’ Error T’𝜖 T’𝜖
F Fid Error Error F(E) Error Error

22. Parsing methods
Parsing
Top down parsing Bottom up parsing (Shift reduce)
Back tracking
Parsing without
backtracking (predictive
parsing)
LR parsing
Operator precedence
LALR
CLR
SLR
Recursive
descent
LL(1)

23. Recursive descent parsing
• A top down parsing that executes a set of recursive procedure to process the
input without backtracking is called recursive descent parser.
• There is a procedure for each non terminal in the grammar.
• Consider RHS of any production rule as definition of the procedure.
• As it reads expected input symbol, it advances input pointer to next position.

24. Example: Recursive descent parsing
Procedure E
{
If lookahead=num
{
Match(num);
T();
}
Else
Error();
If lookahead=$
{
Declare success;
}
Else
Error();
}
Procedure T
{
If lookahead=’*’
{
Match(‘*’);
If lookahead=num
{
Match(num);
T();
}
Else
Error();
}
Else
NULL
}
Proceduce Match(token t)
{
If lookahead=t
lookahead=next_token;
Else
Error();
}
Procedure Error
{
Print(“Error”);
}
E
T
3 * 4 $
num T
num
* T| 𝜖
Success

25. Example: Recursive descent parsing
Procedure E
{
If lookahead=num
{
Match(num);
T();
}
Else
Error();
If lookahead=$
{
Declare success;
}
Else
Error();
}
Procedure T
{
If lookahead=’*’
{
Match(‘*’);
If lookahead=num
{
Match(num);
T();
}
Else
Error();
}
Else
NULL
}
Proceduce Match(token t)
{
If lookahead=t
lookahead=next_token;
Else
Error();
}
Procedure Error
{
Print(“Error”);
}
E
T
num T
num
* T| 𝜖
Success 3 4 * $ Error
3 * 4 $

26. Parsing Methods
Parsing
Top down parsing Bottom up parsing (Shift reduce)
Back tracking
Parsing without
backtracking (predictive
Parsing)
LR parsing
Operator precedence
LALR
CLR
SLR
Recursive
descent
LL(1)

27. Handle & Handle pruning
• Handle: A “handle” of a string is a substring of the string that matches the right
side of a production, and whose reduction to the non terminal of the
production is one step along the reverse of rightmost derivation.
• Handle pruning: The process of discovering a handle and reducing it to
appropriate left hand side non terminal is known as handle pruning.
EE+E
EE*E
Eid
String: id1+id2*id3
Right sentential form Handle Production
id1+id2*id3 id1 Eid
E+id2*id3 id2 Eid
E+E*id3 id3 Eid
E+E*E E*E EE*E
E+E E+E EE+E
E
Rightmost Derivation
E
E+E
E+E*E
E+E*id3
E+id2*id3
id1+id2*id3

28. Shift reduce parser
• The shift reduce parser performs following basic operations:
1. Shift: Moving of the symbols from input buffer onto the stack, this action is
called shift.
2. Reduce: If handle appears on the top of the stack then reduction of it by
appropriate rule is done. This action is called reduce action.
3. Accept: If stack contains start symbol only and input buffer is empty at the
same time then that action is called accept.
4. Error: A situation in which parser cannot either shift or reduce the symbols, it
cannot even perform accept action then it is called error action.

29. Example: Shift reduce parser
Stack Input Buffer Action
$ id+id*id$ Shift
$id +id*id$ Reduce Fid
$F +id*id$ Reduce TF
$T +id*id$ Reduce ET
$E +id*id$ Shift
$E+ id*id$ Shift
$E+id *id$ Reduce Fid
$E+F *id$ Reduce TF
$E+T *id$ Shift
$E+T* id$ Shift
$E+T*id $ Reduce Fid
$E+T*F $ Reduce TT*F
$E+T $ Reduce EE+T
$E $ Accept
Grammar:
EE+T | T
TT*F | F
Fid
String: id+id*id

30. Viable Prefix
• The set of prefixes of right sentential forms that can appear on the stack of a
shift-reduce parser are called viable prefixes.