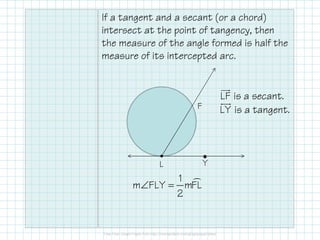
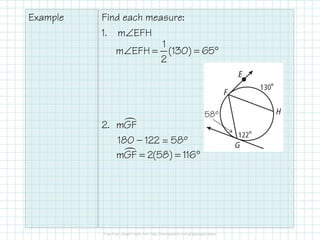
1) When a tangent and secant or chord intersect at the point of tangency, the measure of the angle formed is half the measure of the intercepted arc.
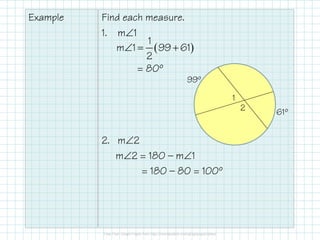
2) When two secants or chords intersect in the interior of a circle, the measure of each angle formed is half the sum of the intercepted arcs.
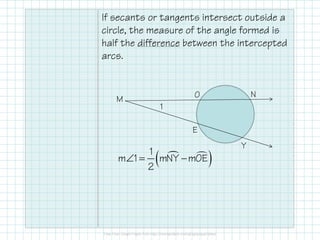
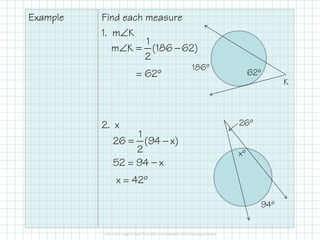
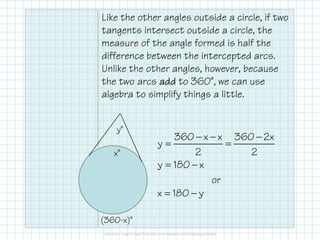
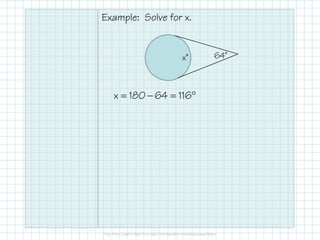
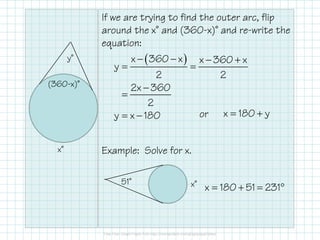
3) When secants or tangents intersect outside a circle, the measure of the angle formed is half the difference between the intercepted arcs. Algebraic formulas are provided to calculate angle measures using the intercepted arcs.