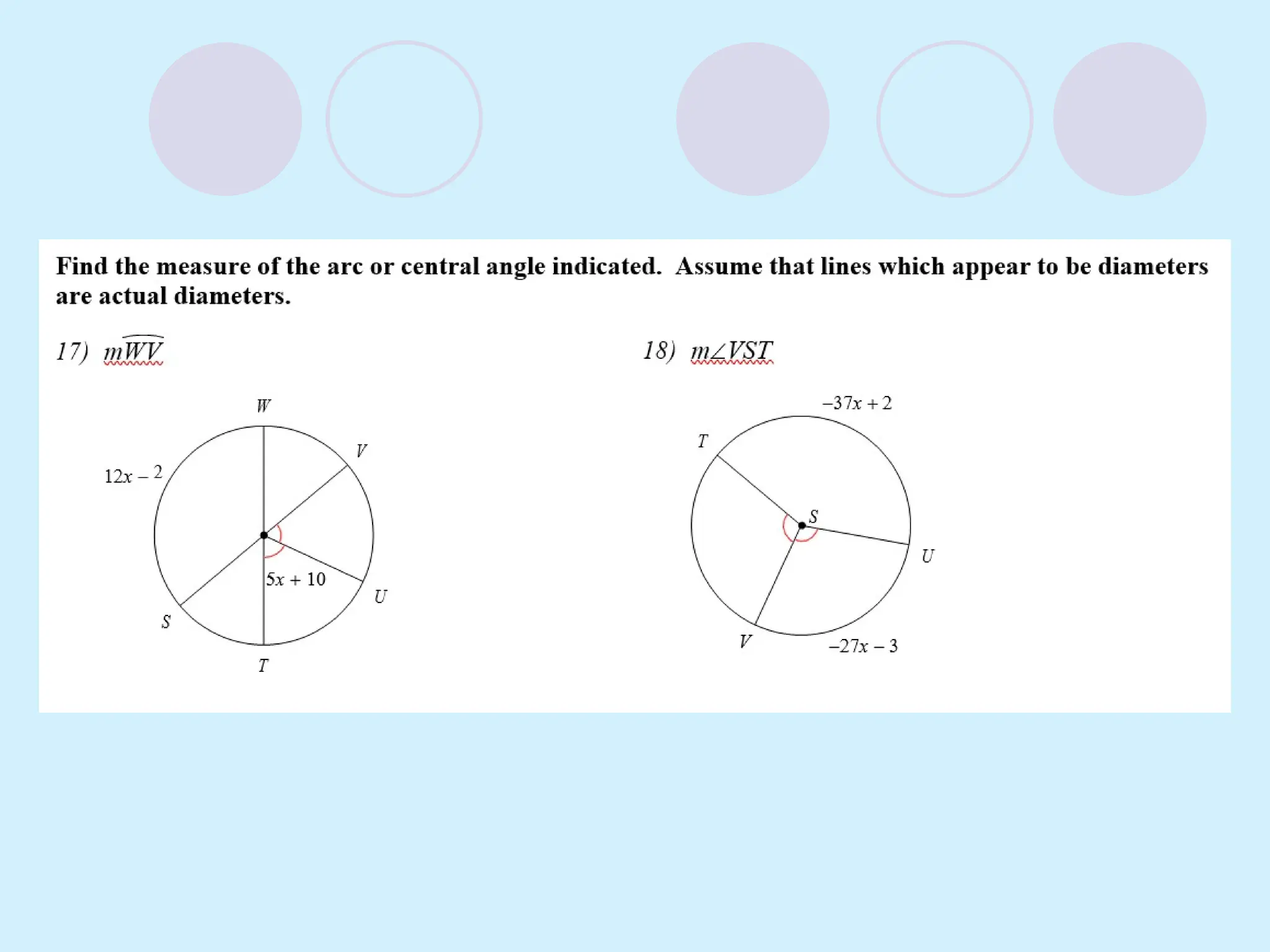
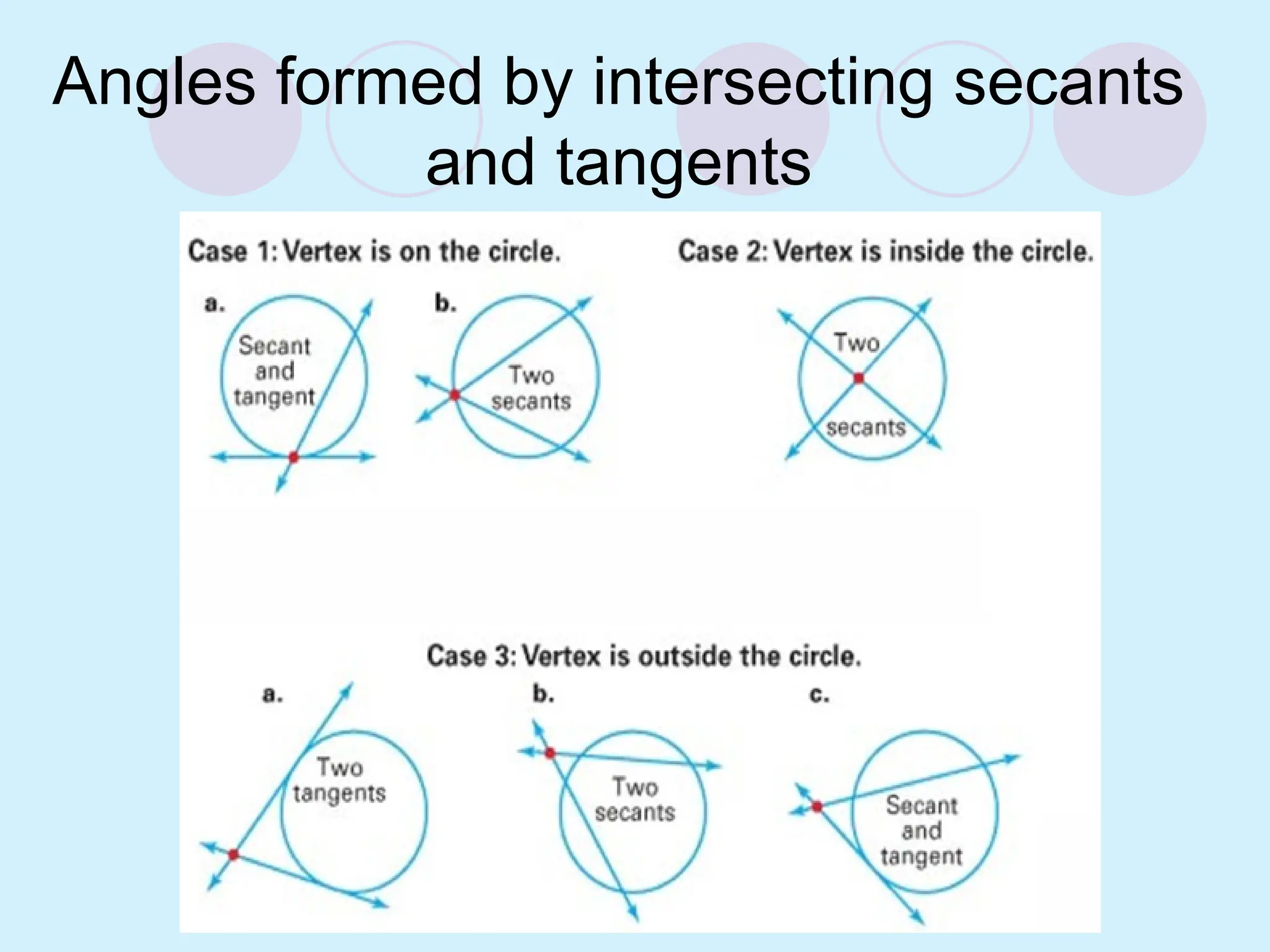
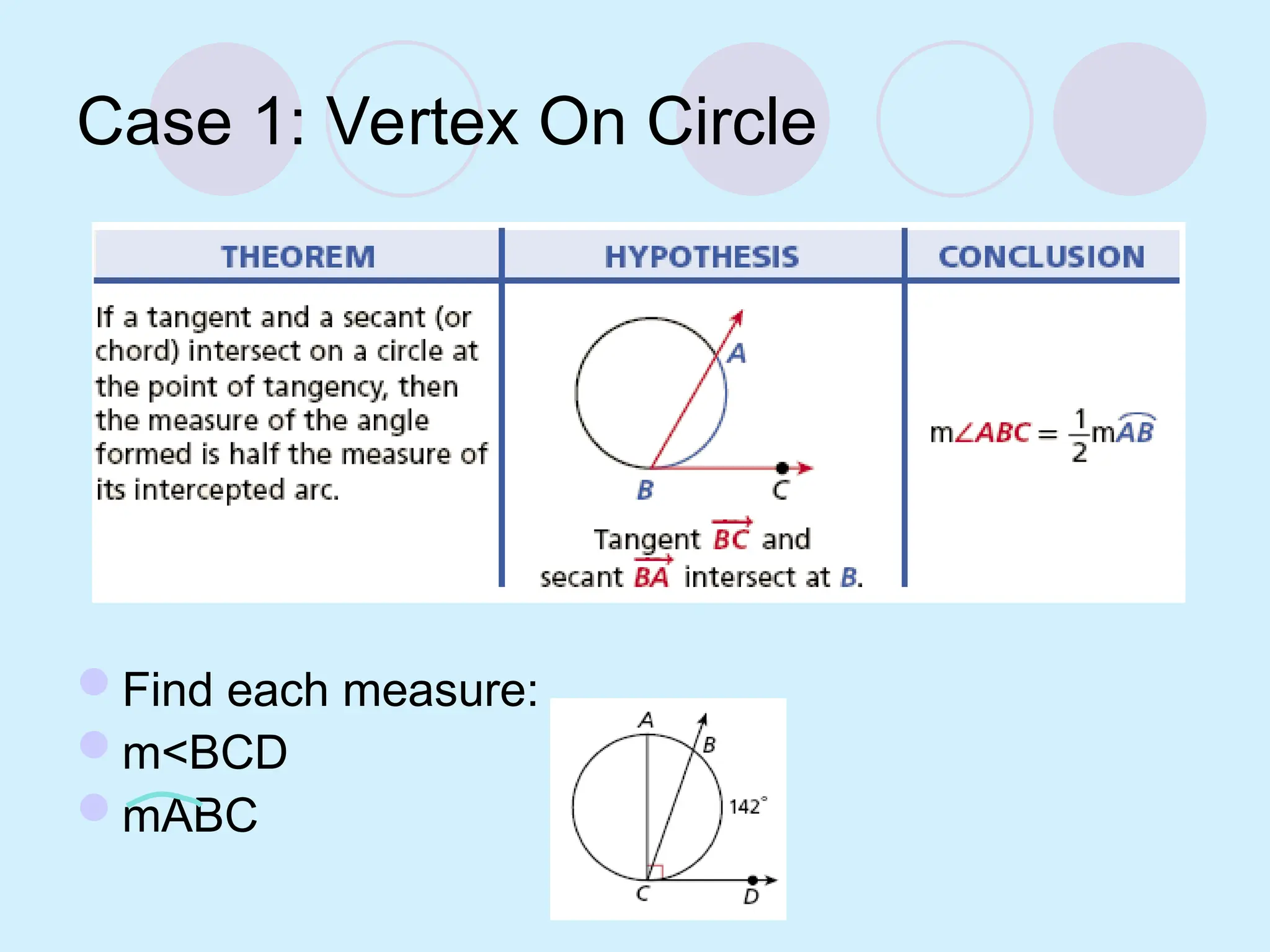
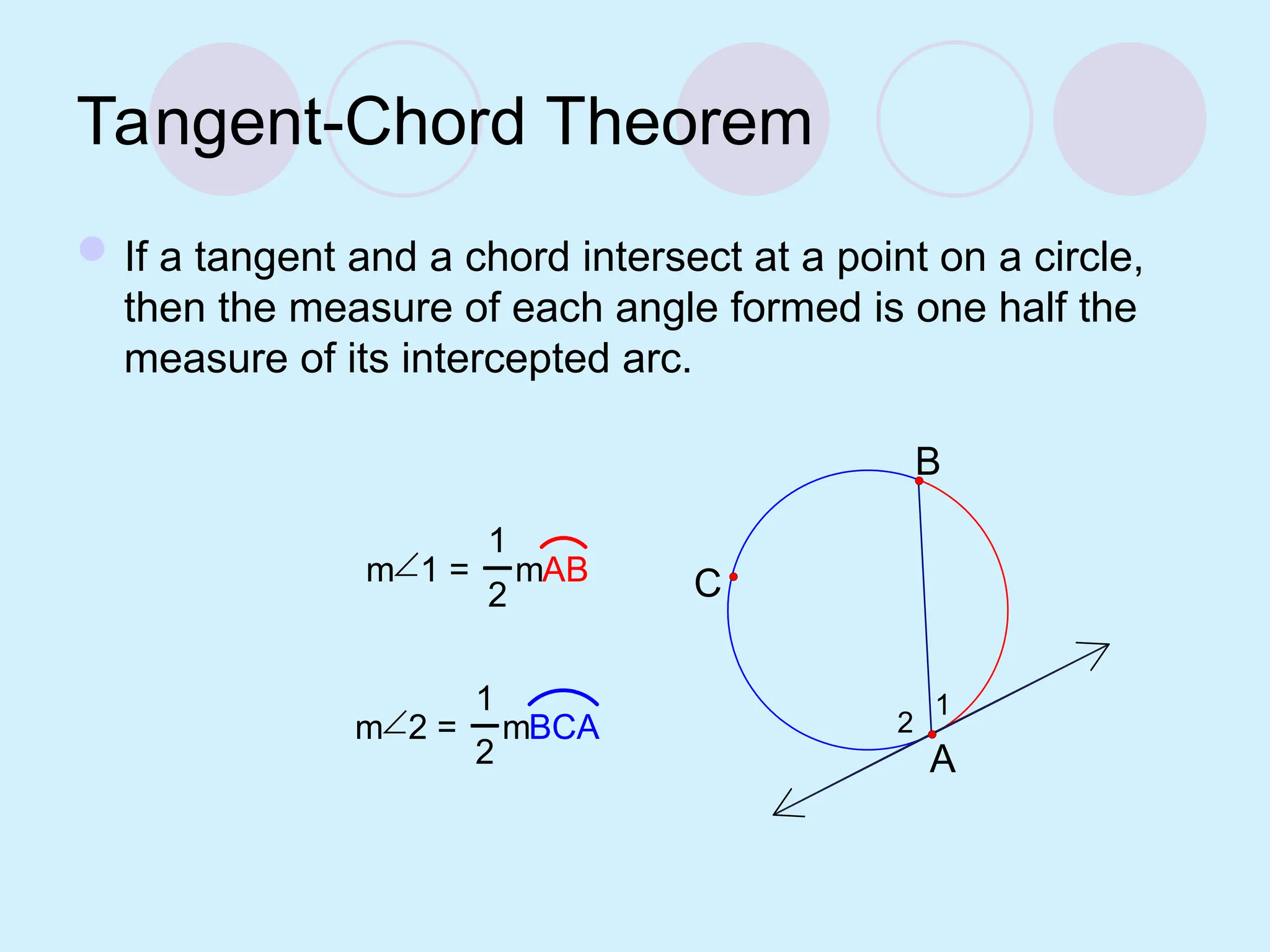
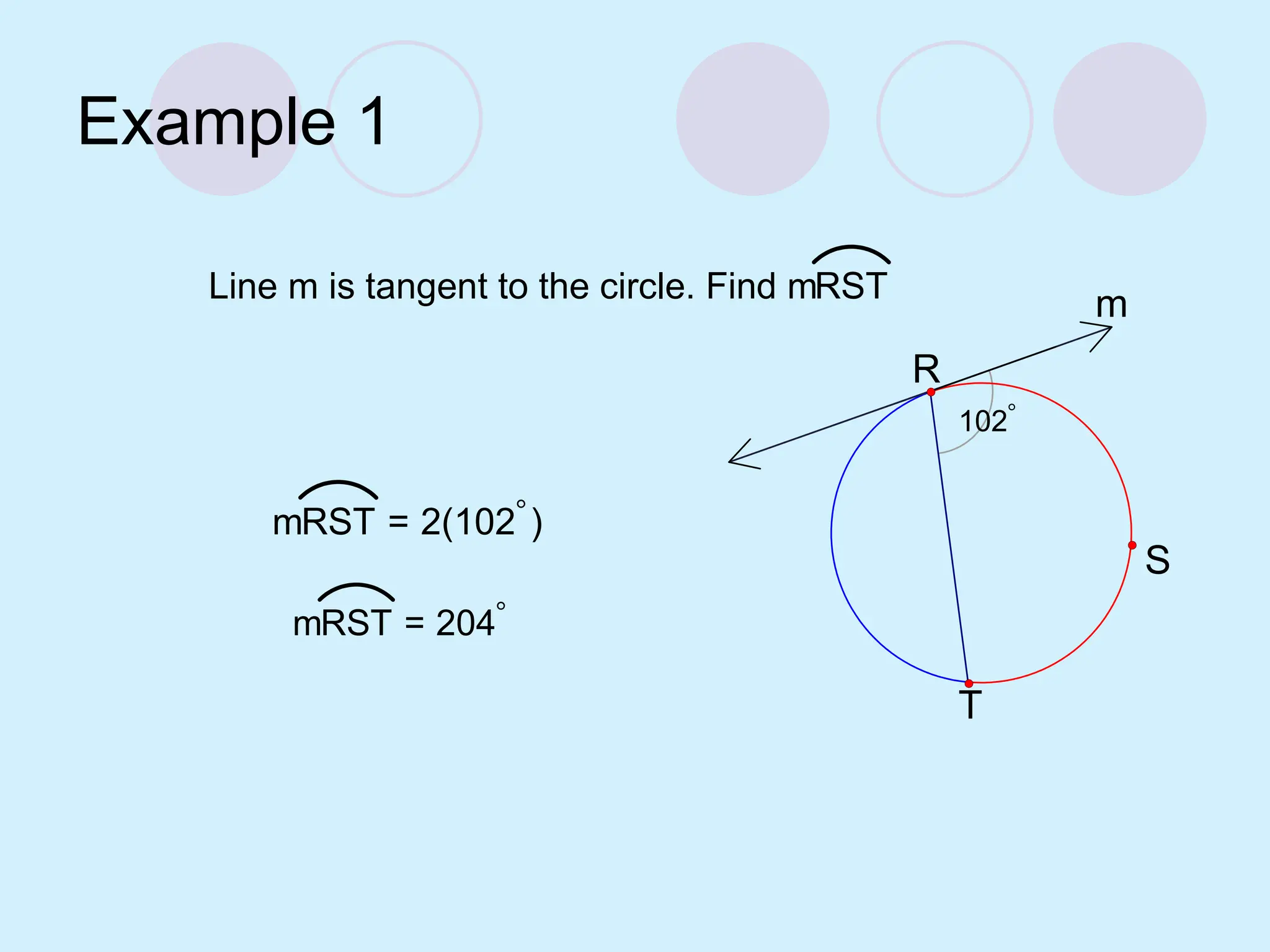
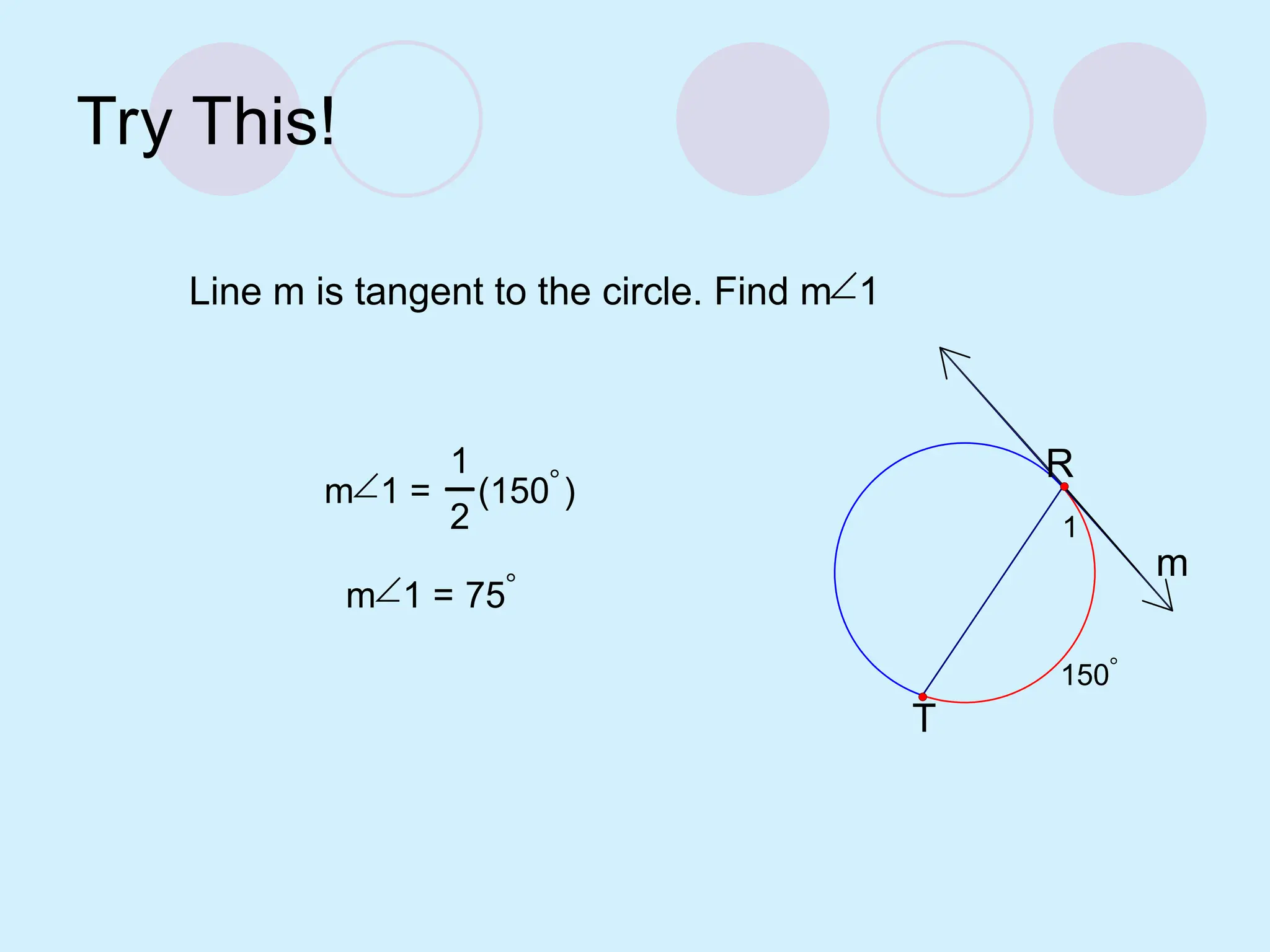
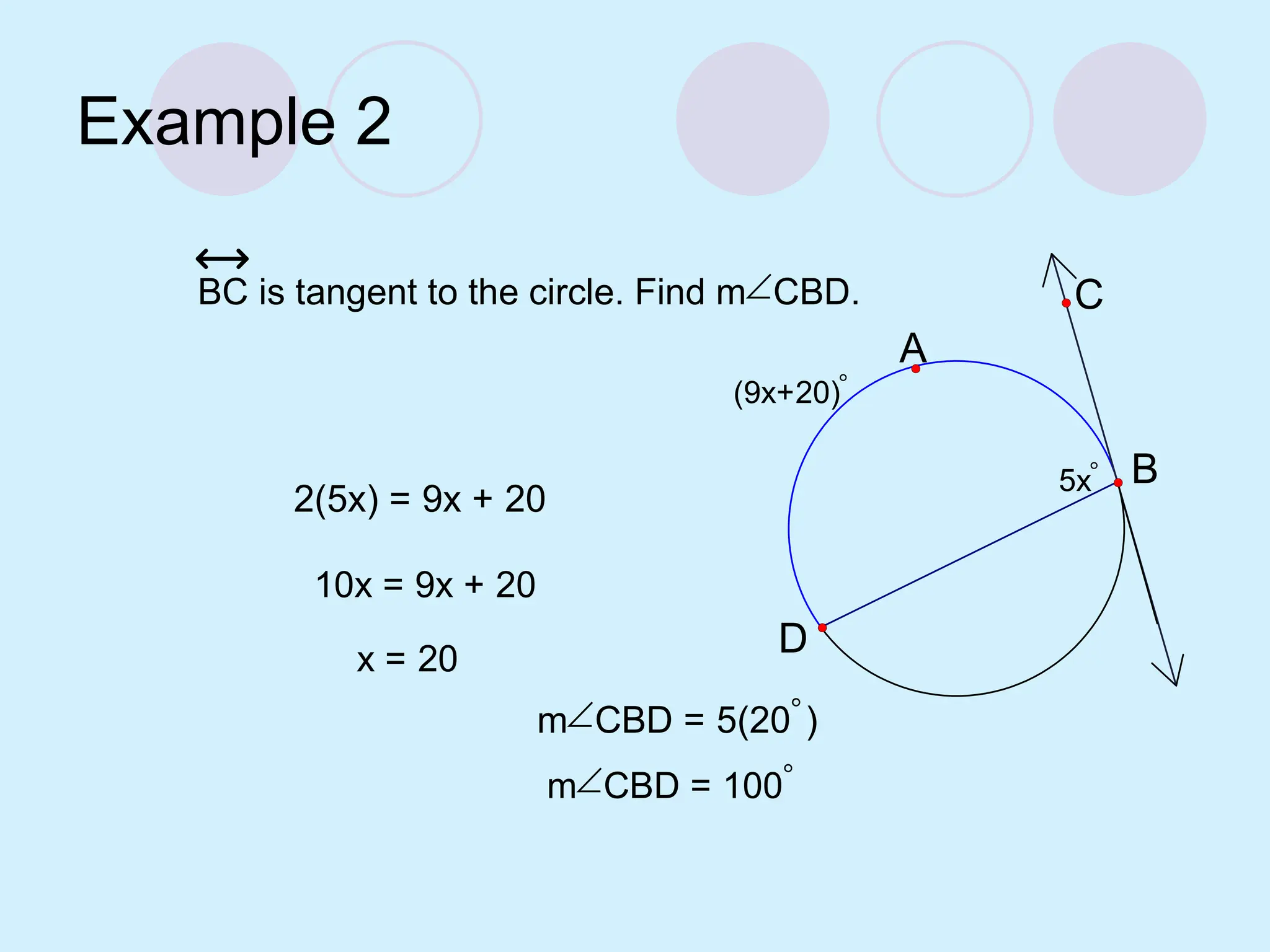
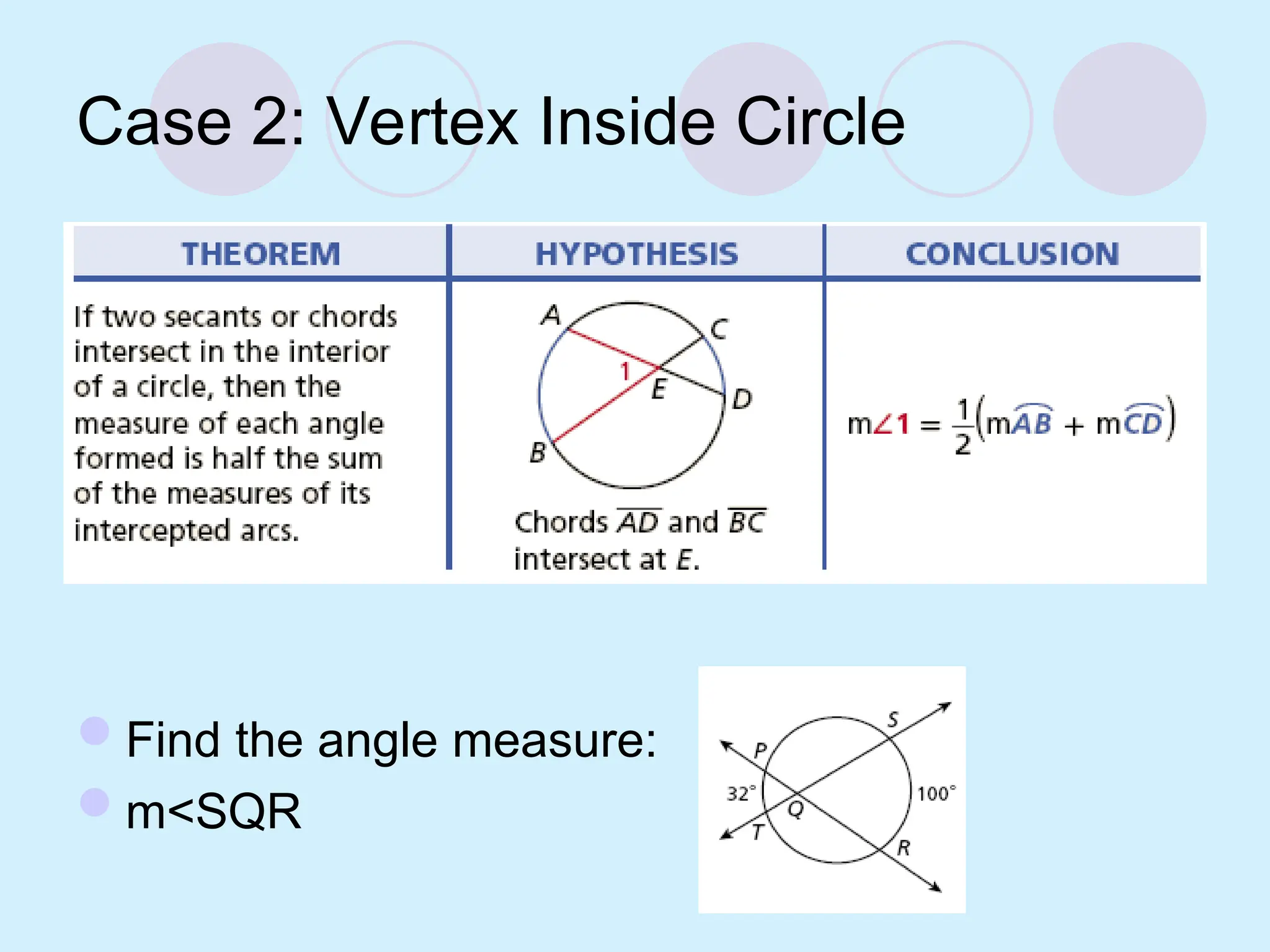
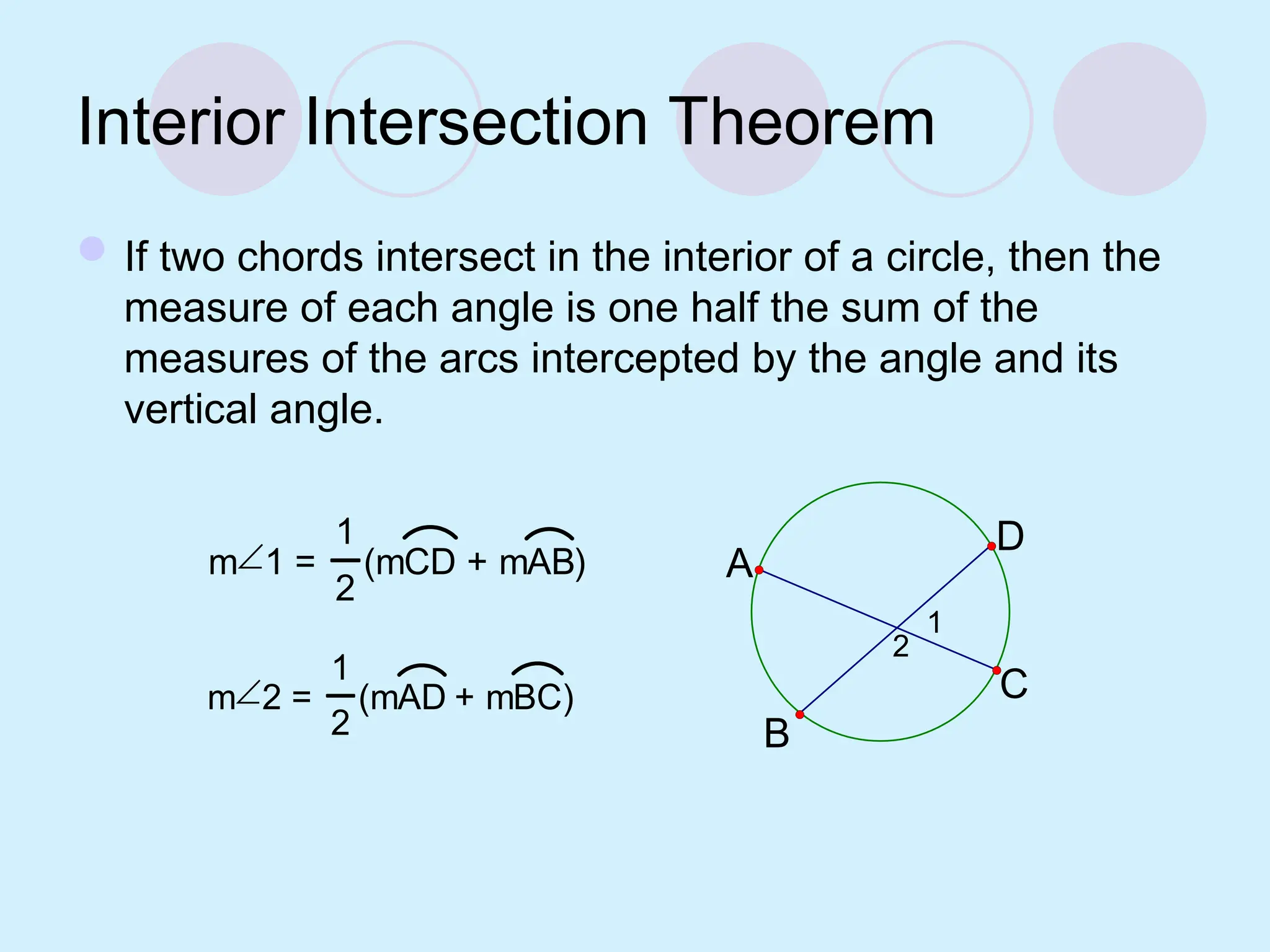
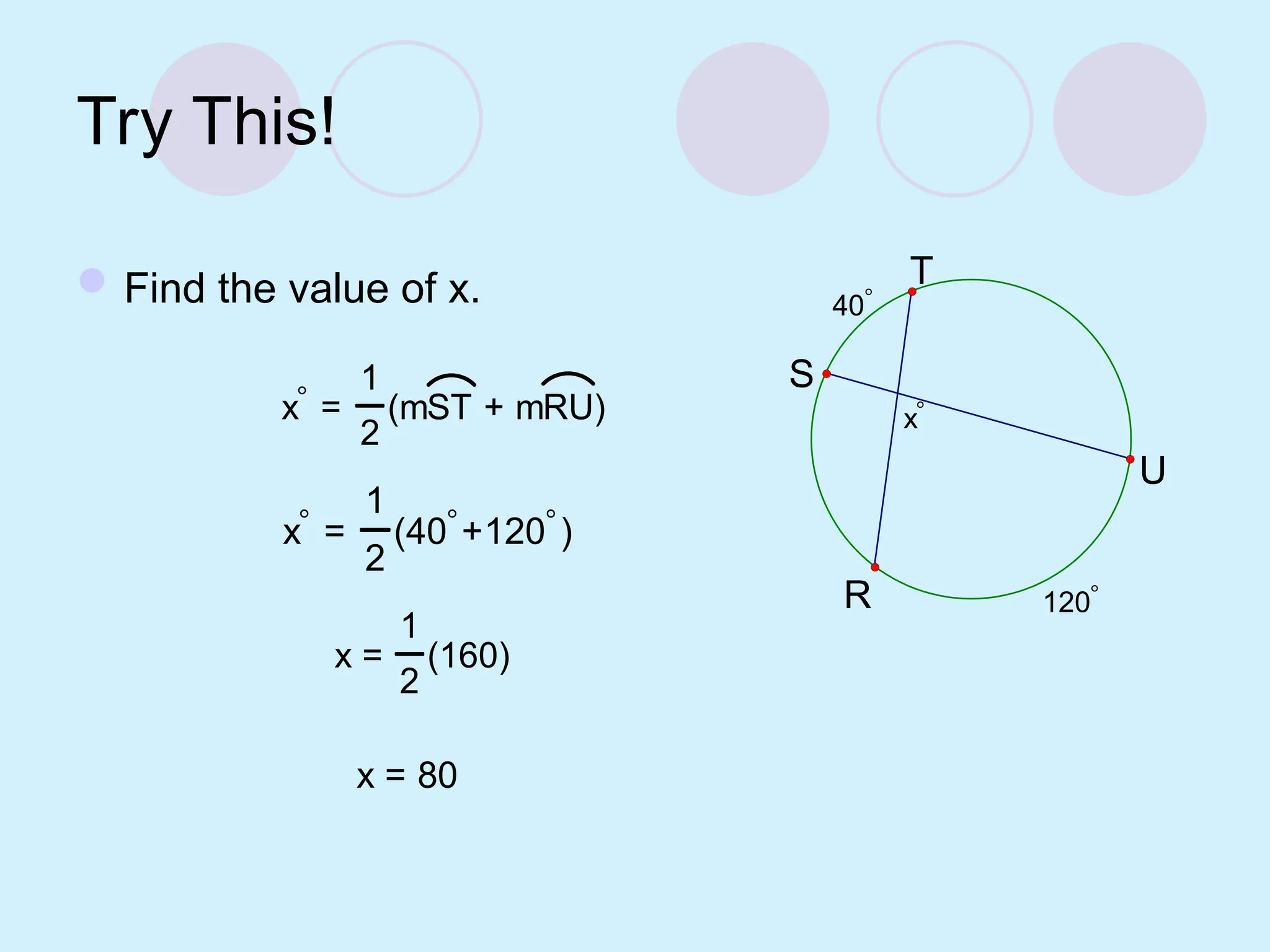
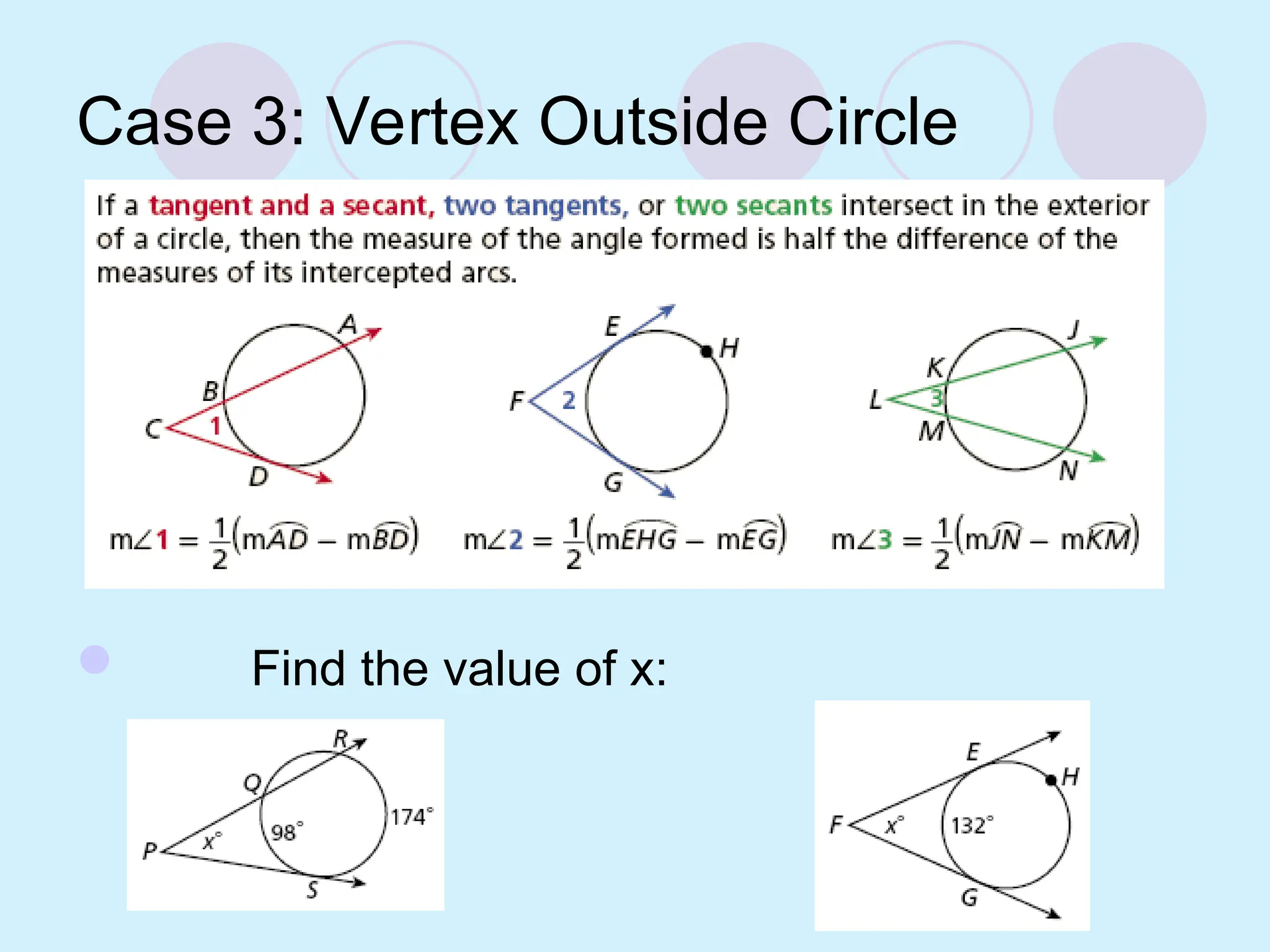
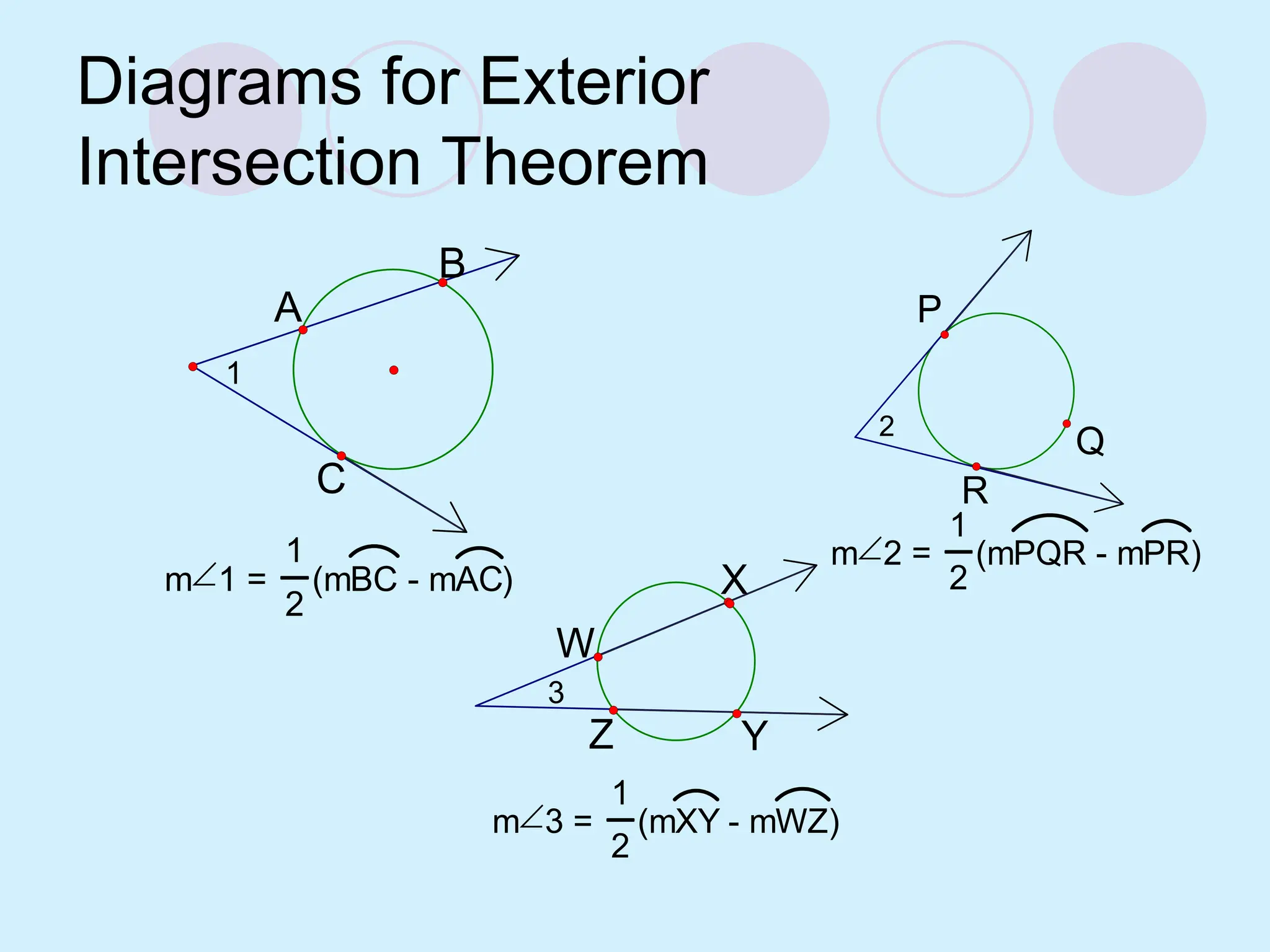
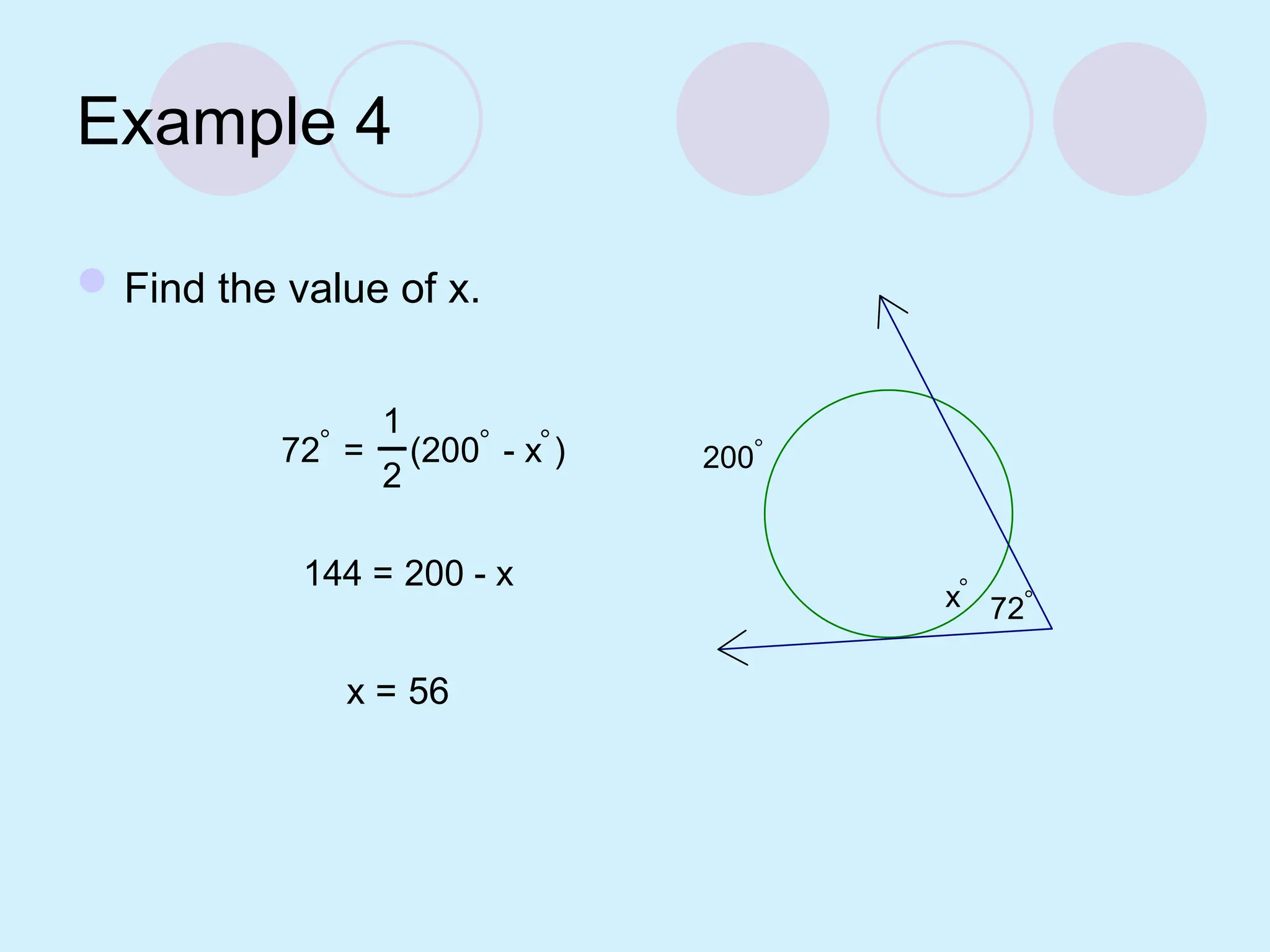
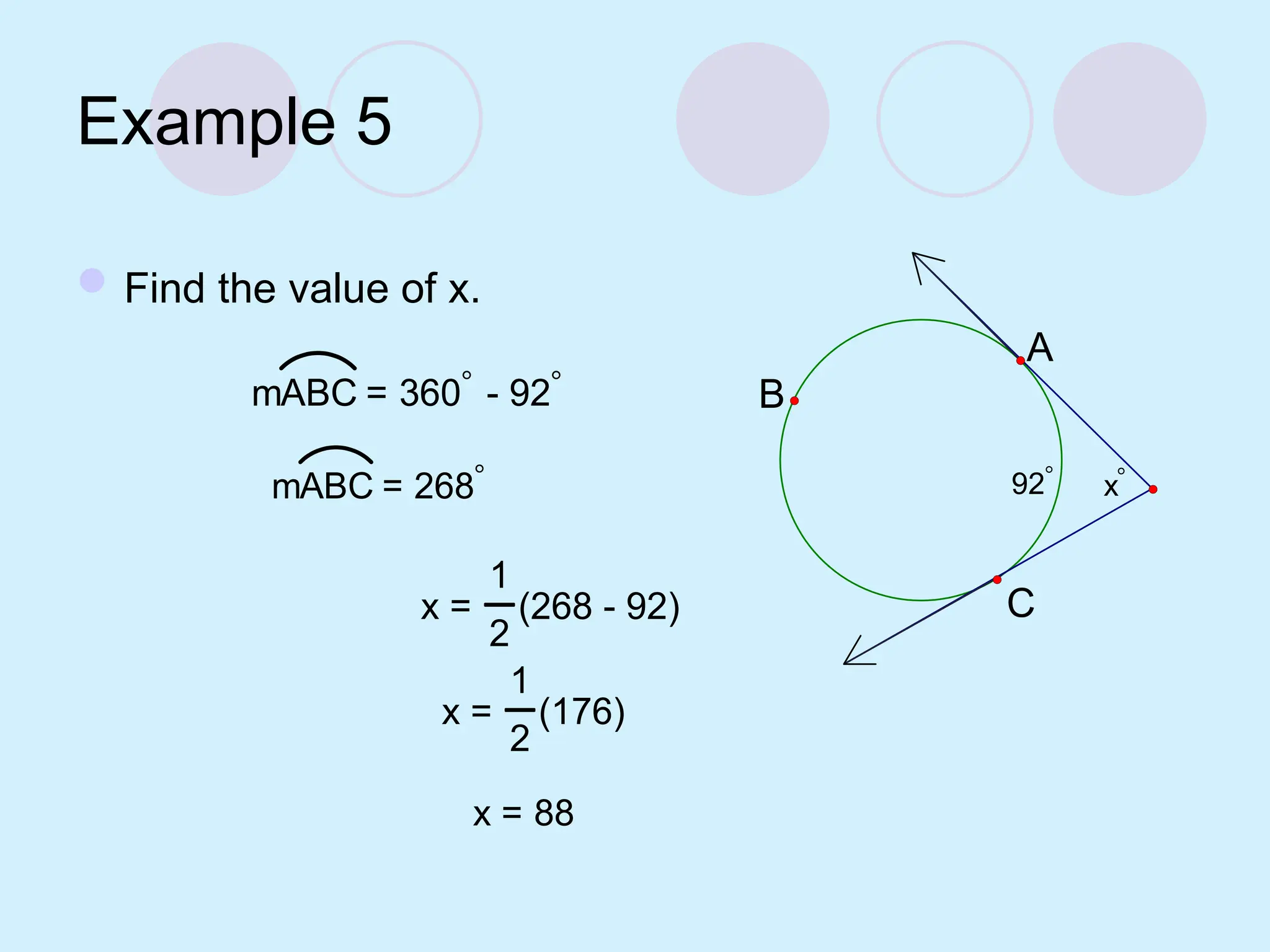
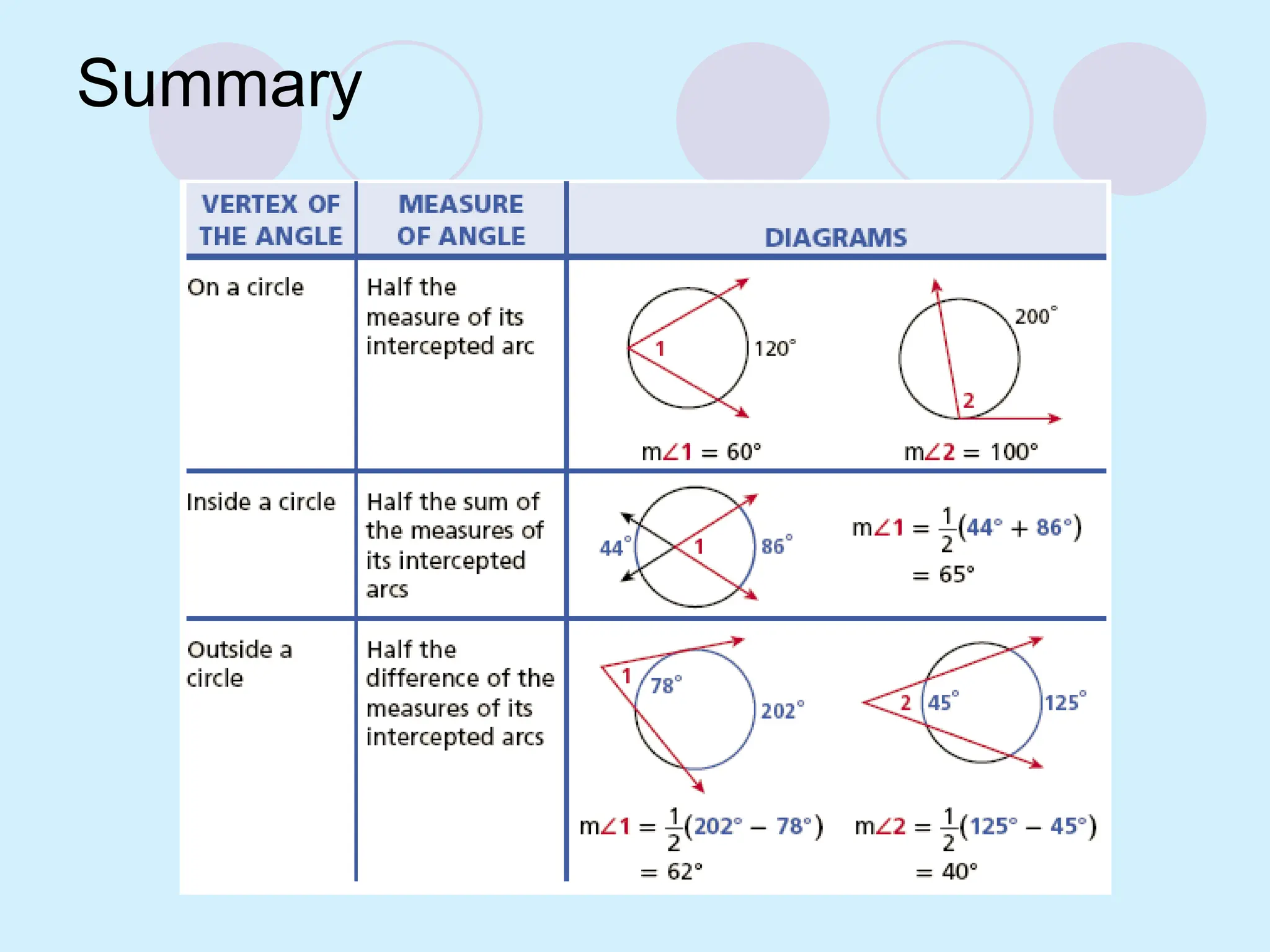
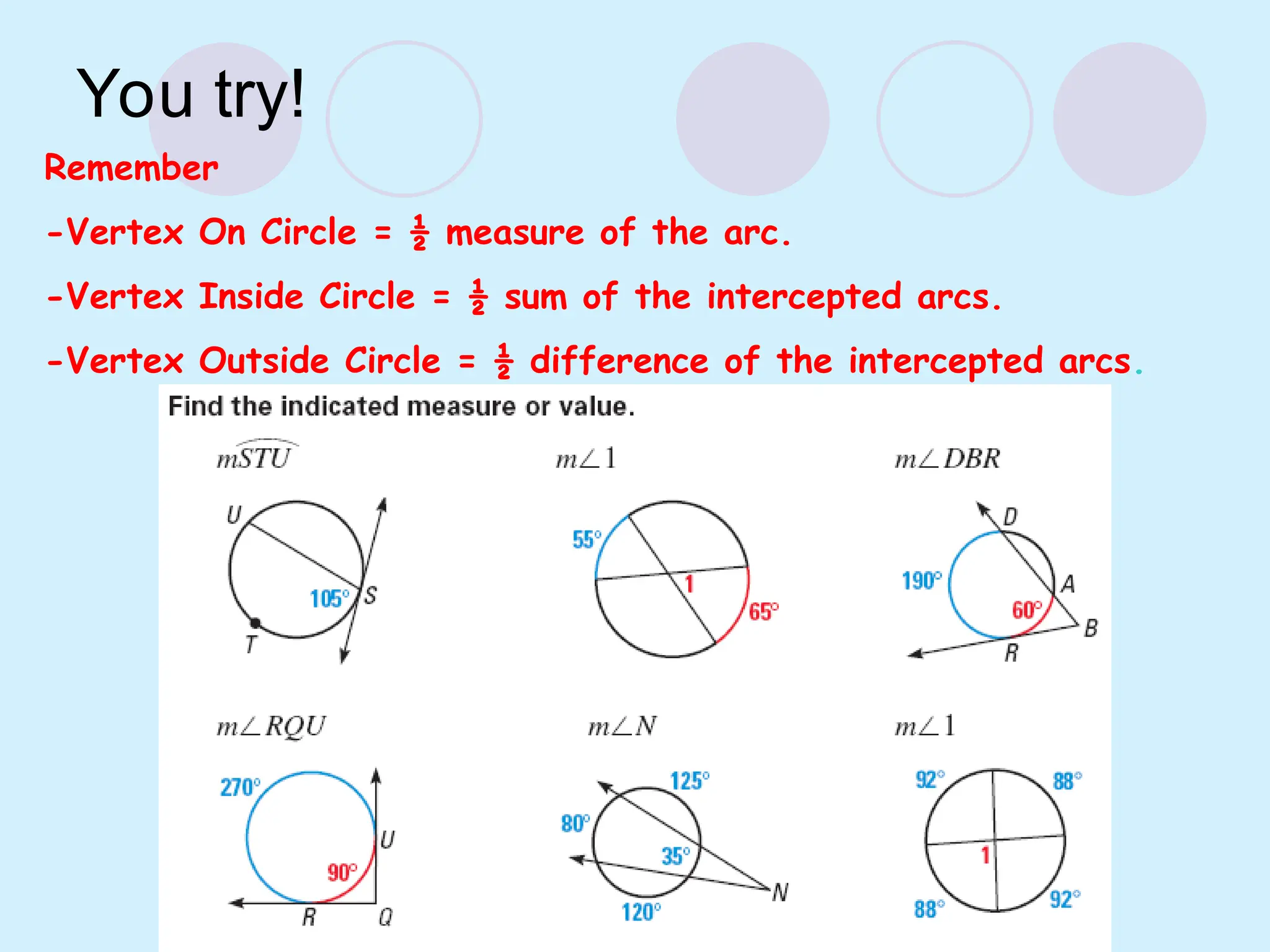
The document defines key concepts related to circles, including tangent lines, common tangents, and angles formed by secants and tangents. It details rules for calculating angles based on the position of the vertex in relation to the circle, including cases for vertices on the circle, inside the circle, and outside the circle. The document also provides examples and theorems to illustrate these concepts.

2. b.secant
Recall:
1. Define:
a. tangent
a line in the plane of a circle that
intersects the circle in exactly one point.
a line in the plane of a circle
that intersects the circle in exactly
one point.

3. c. Tangent circles
coplanar circles that intersect in
one point
d. Concentric circles
coplanar circles that have the
same center.
e. Common tangent
a line or segment that is tangent
to two coplanar circles

4. f. Common internal tangent
intersects the segment that joins
the centers of the two circles
g. Commonexternal tangent
does not intersect the segment
that joins the centers of the two
circles

5. h. Point of tangency
the point at which a tangent line intersects
the circle to which it is tangent

6. Angles formed by intersecting secants
and tangents

7. Case 1: Vertex On Circle
Find each measure:
m<BCD
mABC

8. Tangent-Chord Theorem
If a tangent and a chord intersect at a point on a circle,
then the measure of each angle formed is one half the
measure of its intercepted arc.
2
1
B
A
C
m1 =
1
2
mAB
m2 =
1
2
mBCA

9. Example 1
m
102
T
R
S
Line m is tangent to the circle. Find mRST
mRST = 2(102)
mRST = 204

10. Try This!
Line m is tangent to the circle. Find m1
m
150
1
T
R
m1 =
1
2
(150)
m1 = 75

11. Example 2
(9x+20)
5x
D
B
C
A
BC is tangent to the circle. Find mCBD.
2(5x) = 9x + 20
10x = 9x + 20
x = 20
mCBD = 5(20)
mCBD = 100

12. Case 2: Vertex Inside Circle
Find the angle measure:
m<SQR

13. Interior Intersection Theorem
If two chords intersect in the interior of a circle, then the
measure of each angle is one half the sum of the
measures of the arcs intercepted by the angle and its
vertical angle.
m1 =
1
2
(mCD + mAB)
m2 =
1
2
(mAD + mBC)
2
1
A
C
D
B

14. Example 3
Find the value of x.
174
106
x
P
R
Q
S
x =
1
2
(mPS + mRQ)
x =
1
2
(106+174)
x =
1
2
(280)
x = 140

15. Try This!
Find the value of x.
120
40
x
T
R
S
U
x =
1
2
(mST + mRU)
x =
1
2
(40+120)
x =
1
2
(160)
x = 80

16. Case 3: Vertex Outside Circle
 Find the value of x:

17. Exterior Intersection Theorem
If a tangent and a secant, two tangents, or
two secants intersect in the exterior of a
circle, then the measure of the angle
formed is one half the difference of the
measures of the intercepted arcs.

18. Diagrams for Exterior
Intersection Theorem
1
B
A
C
m1 =
1
2
(mBC - mAC)
2
P
R
Q
m2 =
1
2
(mPQR - mPR)
3
X
W
Y
Z
m3 =
1
2
(mXY - mWZ)

19. Example 4
Find the value of x.
200
x
72
72 =
1
2
(200 - x)
144 = 200 - x
x = 56

20. Example 5
Find the value of x.
mABC = 360 - 92
mABC = 268 x
92
C
A
B
x =
1
2
(268 - 92)
x =
1
2
(176)
x = 88

21. Summary

22. You try!
Remember
-Vertex On Circle = ½ measure of the arc.
-Vertex Inside Circle = ½ sum of the intercepted arcs.
-Vertex Outside Circle = ½ difference of the intercepted arcs.