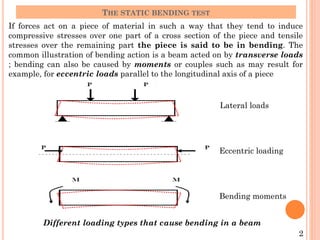
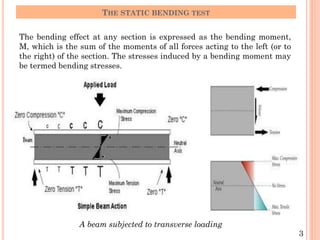
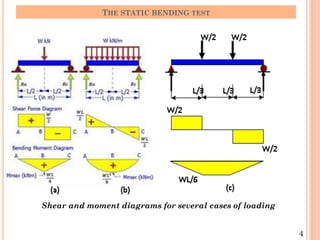
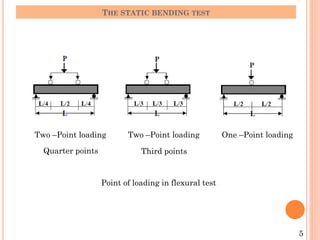
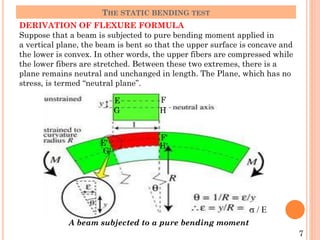
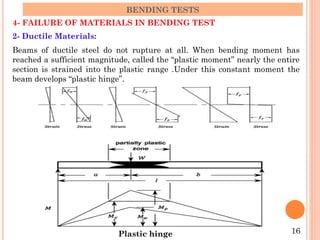
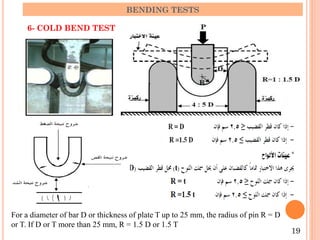
The document describes the static bending test process. It discusses how a beam undergoes bending when subjected to transverse loads, inducing compressive and tensile stresses. The bending moment is expressed as the sum of the moments acting to one side of a beam section. Failure modes depend on the material's ductility - brittle materials rupture suddenly while ductile materials develop plastic hinges. Test variables like loading type, specimen dimensions, and test speed affect bending strength values. Cold bending and hot bending tests evaluate ductility.

1. STATIC BENDING TEST

2. THE STATIC BENDING TEST
If forces act on a piece of material in such a way that they tend to induce
compressive stresses over one part of a cross section of the piece and tensile
stresses over the remaining part the piece is said to be in bending. The
common illustration of bending action is a beam acted on by transverse loads
; bending can also be caused by moments or couples such as may result for
example, for eccentric loads parallel to the longitudinal axis of a piece
Different loading types that cause bending in a beam
Lateral loads
Eccentric loading
Bending moments
2

3. THE STATIC BENDING TEST
The bending effect at any section is expressed as the bending moment,
M, which is the sum of the moments of all forces acting to the left (or to
the right) of the section. The stresses induced by a bending moment may
be termed bending stresses.
A beam subjected to transverse loading
3

4. THE STATIC BENDING TEST
Shear and moment diagrams for several cases of loading
4

5. THE STATIC BENDING TEST
One –Point loading
Third points
Two –Point loading
Two –Point loading
Quarter points
Point of loading in flexural test
5

6. THE STATIC BENDING TEST
1-ASSUMPTION IN SIMPLE BENDING THEORY
1- Transverse sections of the beam which are plane before bending will
remain plane during bending.
2- From condition of symmetry during bending transverse sections will be
perpendicular to circular arcs having a common center of curvature.
3- The radius of curvature of the beam during bending is large compared
with transverse dimensions.
4- Longitudinal elements of the beam are subjected only to simple tension
or compression and there is no lateral stress (pure bending moment).
5- Young’s modulus for the beam material has the same value in tension
and compression.
Because the loads required to cause failure may be relatively small and
easily applied, bending tests can often be made with simple and
inexpensive apparatus. Because the deflections in bending tests are
many times the elongation in tension tests, a reasonable determination of
stiffness or resilience can be made with less sensitive and less expensive
instruments than are required in a tension test. Thus the bending test
is often used as a control test for brittle materials, notably cast iron
and concrete.
6

7. THE STATIC BENDING TEST
A beam subjected to a pure bending moment
s / E
E'
F'
F
E
G H
G'
H'
DERIVATION OF FLEXURE FORMULA
Suppose that a beam is subjected to pure bending moment applied in
a vertical plane, the beam is bent so that the upper surface is concave and
the lower is convex. In other words, the upper fibers are compressed while
the lower fibers are stretched. Between these two extremes, there is a
plane remains neutral and unchanged in length. The Plane, which has no
stress, is termed “neutral plane”.
7

8. THE STATIC BENDING TEST
Deformation in bending
During bending EF stretches to become E'F', but GH being at the neutral
axis is unstrained when it becomes G'H',
G'H' = GH = δx = R δθ
E'F' = (R+Y) δθ
The longitudinal strain in fiber E'F' is εx =
but EF = GH = G'H' = R δθ ; therefore
εx =
hence εx = Y/R (1)
Stress-strain relationship
εx = sx / E (2)
εx = Y/R = sx / E
Then sx/Y= E/R (3)
E ' F '- E F
E F
(R+Y) δθ – R δθ
Rδθ
The summation of the moments about the centroid of the section
(M =0) gives.
y
da
M .
s


da
R
Ey
M
2


Substituting equation (3) in equation (4)
(4)
8

9. THE STATIC BENDING TEST
da
y
R
E
M 2


da
y2

R
EI
M x

x
EI
M
R
l

Represent the second moment of area of the section.
Equation (3) tends to
The bending relationship
The fundamental relationship between bending stress, moment and
geometry of deformation is:
Where
M: applied moment (N.m)
I: second moment of area (m4)
σ: bending stress at y from neutral axis (N/m2)
Y: a distance from the neutral axis to plane of stress (m)
E: Young's modulus (N/m2)
R: radius of curvature (m)
9
Then E/R= M/I and from previous E/R= sx/Y

10. BENDING TESTS
In Fig. (a) the solid line shows the stress variation in a homogeneous
beam of symmetrical section for a material that has the same stress-
strain variation in both tension and compression. The equivalent
linear stress distribution that would yield the same moment is shown
by the dotted line.
If the material does not have the same stress-strain in tension
and compression, the neutral axis must shift toward the stiffer side
of the beam in order to maintain equality of the resultants of the
tensile and compressive forces, as shown in Fig.(b).
10
Bending stresses above the proportional limit

11. BENDING TESTS
2- GENERAL REQUIREMENTS OF BENDING TEST SPECIMENS
a) With respect to type of loadings
There are two common bending test arrangements:
The four point bending (4PB) test is generally preferred Compared to
three point bending (3PB), since it provides a constant moment over a
substantial length of the span. The shear stress in this portion of the beam is
zero.
For this reason, failures occur outside the inner loading points should
be discounted.
b) With respect to shape of cross-section
Circular, squared, or rectangular cross sections may be used.
11

12. BENDING TESTS
c) With respect to relative dimensions
The beam dimensions must be so proportioned that it dose not fail by lateral
buckling or shear failure before the ultimate flexural strength is reached. In
order to avoid shear failure, the span must not be too short with respect to
the depth. Values of L= 6d to 12d, where L = length and d = depth are
generally used. The actual value depends on the material, the shape of beam
and the type of loading.
A value of L< 15b, where b = width, usually safeguards against lateral
buckling.
Apparatus 12

13. 3- MECHANICAL PROPERTIES IN FLEXURAL
BENDING TESTS
1. Proportional limit strength
I
Y
M p
p 
s
MP.L = PP.L × L /4 for 3PB
MP.L = PP.L × L /6 for 4PB
MP.L = PP.L× L for cantilever
L: Beam span.
Y: is the distance from the neutral
axis to an extreme fiber.
Y = h/2 or D/2 (
‫نصف‬
‫ارتفاع‬
‫القطاع‬
)
I: is the second moment of inertia of
cross sectional area (
‫عزم‬
‫القصور‬
‫الذاتى‬
) .
Where Zx equals Ix/y and is called
elastic modulus of the section
h
b
d
2. Ultimate bending strength
or Modulus of rupture
I
Y
Mmax
max 
s
Mmax = Pmax × L/4 for 3PB
Mmax = Pmax × L/6 for 4PB
13
s = M/ZX

14. BENDING TESTS
3- The modulus of elasticity (Stiffness) constant
Δ
P
I
48
PL
E
3




Where, P/ is the slope of straight line portion of the load deflection curve in
the elastic stage.
4- Bending Resilience
Resilience (R) = (½ )  Pp   p
= Area under the straight line in P- curve
Modulus of Resilience = R/Volume
5- Toughness in Bending
Toughness (T) = (2/3) Pmax max
= Total area under the load –deflection curve
Modulus of Toughness = T/Volume
14

15. BENDING TESTS
4- FAILURE OF MATERIALS IN BENDING TEST
1- Brittle Materials:
The failure of beams of brittle material such as
cast iron and plain concrete always occurs by
sudden rupture along a plane perpendicular to
the longitudinal axis.
failure finally occurs in the tensile fibers
because the tensile strength of these materials
is only a fraction of the compressive strength.
The ratio of tensile to compressive strength is
about 25 percent for cast iron and about 10
percent for concrete
15

16. BENDING TESTS
4- FAILURE OF MATERIALS IN BENDING TEST
2- Ductile Materials:
Beams of ductile steel do not rupture at all. When bending moment has
reached a sufficient magnitude, called the “plastic moment” nearly the entire
section is strained into the plastic range .Under this constant moment the
beam develops “plastic hinge”.
Plastic hinge 16

17. 5- EFFECT OF VARIABLES:
BENDING TESTS
1- Loading Type
 In a simple span, the largest value of the modulus of rupture is
obtained from central loading.
 Cantilever loading tests tends to give slightly higher results than
central loading on a simple span.
 Third point loading on a simple span, invariably gives results
somewhat less than central loading (roughly 10 to 25%). These
relations probably hold, at least in principle, for other brittle materials
give the most concordant results.
2- Specimen Dimensions
 Tests of both cast iron and concrete have shown that for beams of the
same cross section, the shorter the span length, the greater the
modulus of rupture.
 The shorter the span, the less is the computed value of the modulus
of elasticity of cast iron, although the difference is not over about 10%
for length diameter ratios ranging 10 to 30.
 With increasing the depth, the modulus of rupture decreases. Where
the gradient of stress make large area expose to high stress, Therefore
strength decreases 17
max
s
L
max
s
D
L E

18. BENDING TESTS
4- Test Speeds
The greater the speed, the higher the indicated
strength.
3- Effect of specimen shape
With the same area
6- COLD BEND TEST (for ductile materials)
7- A HOT BEND TEST
Is sometimes made, for example, on wrought iron by heating it to welding
temperature (about 1000oC) and bending the heated piece on an anvil, the
test serves to detect too high a sulphur content.
18
Cold bend test is sometimes made to check the ductility for particular types of
service or to detect loss of ductility under certain types of treatment, may
serve to detect too high a carbon or phosphorous content

19. BENDING TESTS
19
6- COLD BEND TEST
For a diameter of bar D or thickness of plate T up to 25 mm, the radius of pin R = D
or T. If D or T more than 25 mm, R = 1.5 D or 1.5 T

20. 20
BENDING TESTS

21. THANK YOU