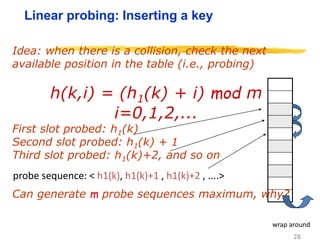
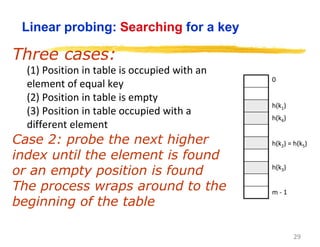
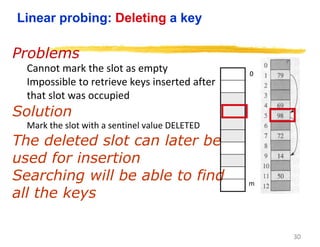
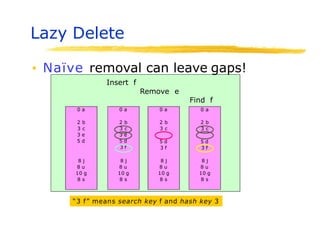
Hashing is a technique used to map data of arbitrary size to values of fixed size. It allows for fast lookup of data in near constant time. Common applications include dictionaries, databases, and search engines. Hashing works by applying a hash function to a key that returns an index value. Collisions occur when different keys hash to the same index, and must be resolved through techniques like separate chaining or open addressing.

1. Hashing

2. 2
The Search Problem
Find items with keys matching a given
search key
Given an array A, containing n keys, and a
search key x, find the index i such as x=A[i]
As in the case of sorting, a key could be part
of a large record.

3. 3
Applications
Keeping track of customer account
information at a bank
Search through records to check balances and perform
transactions
Keep track of reservations on flights
Search to find empty seats, cancel/modify reservations
Search engine
Looks for all documents containing a given word

4. 4
Special Case: Dictionaries
Dictionary = data structure that supports
mainly two basic operations: insert a
new item and return an item with a given
key
Queries: return information about the
set S:
Search (S, k)
Minimum (S), Maximum (S)
Successor (S, x), Predecessor (S, x)
Modifying operations: change the set
Insert (S, k)
Delete (S, k) – not very often

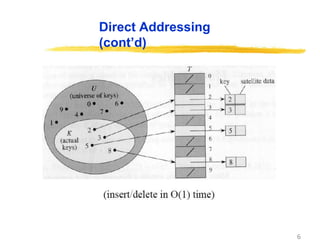
5. 5
Direct Addressing
Assumptions:
Key values are distinct
Each key is drawn from a universe U = {0, 1, . . . , m - 1}
Idea:
Store the items in an array, indexed by keys
• Direct-address table representation:
– An array T[0 . . . m - 1]
– Each slot, or position, in T corresponds to a key in U
– For an element x with key k, a pointer to x (or x itself) will be placed
in location T[k]
– If there are no elements with key k in the set, T[k] is empty,
represented by NIL

6. 6
Direct Addressing
(cont’d)

7. 7
Operations
Alg.: DIRECT-ADDRESS-SEARCH(T, k)
return T[k]
Alg.: DIRECT-ADDRESS-INSERT(T, x)
T[key[x]] ← x
Alg.: DIRECT-ADDRESS-DELETE(T, x)
T[key[x]] ← NIL
Running time for these operations: O(1)

8. 8
Comparing Different
Implementations
Implementing dictionaries using:
Direct addressing
Ordered/unordered arrays
Ordered/unordered linked lists
Inser
t
Search
ordered array
ordered list
unordered array
unordered list
O(N)
O(N)
O(N)
O(N)
O(1)
O(1)
O(lgN)
O(N)
direct addressing O(1) O(1)

9. Why do we need hashing?
▪ Many applications deal with lots of data
➢Search engines and web pages
▪ There are myriad look ups.
▪ The look ups are time critical.
▪ Typical data structures like arrays and
lists, may not be sufficient to handle
efficient lookups
▪ In general: When look-ups need to
occur in near constant time. O(1)

10. Why do we need hashing?
▪ Consider the internet(2002 data):
➢By the Internet Software Consortium
survey at http://www.isc.org/ in 2001
there are 125,888,197 internet hosts,
and the number is growing by 20%
every six month!
➢Using the best possible binary
search it takes on average 27
iterations to find an entry.
➢By an survey by NUA at
http://www.nua.ie/ there are 513.41
million users world wide.

11. Why do we need hashing?
▪ We need something that can do
better than a binary search,
O(log N).
▪ We want, O(1).
Solution: Hashing
In fact hashing is used in:
Web searches Spell checkers Databases
Compilers passwords Many others

12. Building an index using HashMaps
WORD NDOCS PTR
jezebel 20
jezer 3
jezerit 1
jeziah 1
jeziel 1
jezliah 1
jezoar 1
jezrahliah 1
jezreel 39
jezoar
34 6 1 118 2087 3922 3981 5002
44 3 215 2291 3010
56 4 5 22 134 992
DOCID OCCUR POS 1 POS 2 . . .
566 3 203 245 287
67 1 132
. . .
More on this in Graphs…

13. The concept
▪ Suppose we need to find a better
way to maintain a table
(Example: a Dictionary) that is
easy to insert and search in
O(1).

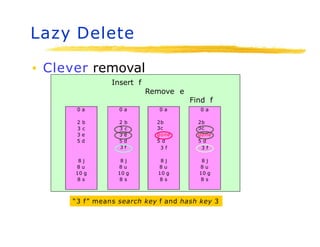
14. Big Idea in Hashing
▪ Let S={a1,a2,…am} be a set of objects that
we need to map into a table of size N.
➢Find a function such that H:S [1…n]
➢Ideally we’d like to have a 1-1 map
➢But it is not easy to find one
➢Also function must be easy to compute
➢It is a good idea to pick a prime as the table
size to have a better distribution of values
▪ Assume ai is a 16-bit integer.
➢Of course there is a trivial map H(ai)=ai
➢But this may not be practical. Why?

15. Finding a hash Function
▪ Assume that N = 5 and the values
we need to insert are: cab, bea, bad
etc.
▪ Let a=0, b=1, c=2, etc
▪ Define H such that
➢H[data] = (∑ characters) Mod N
▪ H[cab] = (2+0+1) Mod 5 = 3
▪ H[bea] = (1+4+0) Mod 5 = 0
▪ H[bad] = (1+0+3) Mod 5 = 4

16. Collisions
▪ What if the values we need to insert
are “abc”, “cba”, “bca” etc…
➢They all map to the same location
based on our map H (obviously H is not a good
hash map)
▪ This is called “Collision”
▪ When collisions occur, we need to
“handle” them
▪ Collisions can be reduced with a selection
of a good hash function

17. Choosing a Hash Function
▪ A good hash function must
➢Be easy to compute
➢Avoid collisions
▪ How do we find a good hash function?
▪ A bad hash function
➢Let S be a string and H(S) = Σ Si where Si is the ith
character of S
➢Why is this bad?

18. Choosing a Hash Function?
▪ Question
➢Think of hashing 10000, 5-letter words into a
table of size 10000 using the map H defined as
follows.
➢H(a0a1a2a3a4) = Σ ai (i=0,1….4)
➢If we use H, what would be the key
distribution like?

19. Choosing a Hash Function
▪ Suppose we need to hash a set of strings
S ={Si} to a table of size N
▪ H(Si) = ( Si[j].dj ) mod N, where Si[j] is
the jth character of string Si
➢How expensive is to compute this function?
• cost with direct calculation
• Is it always possible to do direct calculation?
➢Is there a cheaper way to calculate this? Hint:
use Horners Rule.

20. Collisions
▪ Hash functions can be many-to-1
➢They can map different search keys
to the same hash key.
hash1(`a`) == 9 == hash1(`w`)
▪ Must compare the search key with
the record found
➢If the match fails, there is a collision

21. Collision Resolving strategies
▪ Separate chaining
▪ Open addressing
➢Linear Probing
➢Quadratic Probing
➢Double Probing
➢Etc.

22. Separate Chaining
▪ Collisions can be resolved by
creating a list of keys that map to
the same value

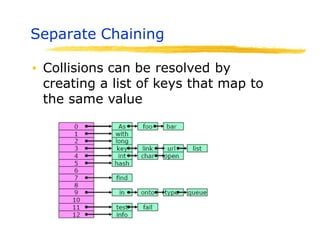
23. Separate Chaining
▪ Use an array of linked lists
➢LinkedList[ ] Table;
➢Table = new LinkedList(N), where N is the
table size
▪ Define Load Factor of Table as
➢ = number of keys/size of the table
( can be more than 1)
▪ Still need a good hash function to
distribute keys evenly
➢For search and updates

24. 24
Common Open Addressing Methods
Linear probing
Quadratic probing
Double hashing
Note: None of these methods
can generate more than m2
different probing sequences!

25. Linear Probing
▪ The idea:
➢Table remains a simple array of size N
➢On insert(x), compute f(x) mod N,
if the cell is full, find another by
sequentially searching for the next
available slot
• Go to f(x)+1, f(x)+2 etc..
➢On find(x), compute f(x) mod N, if
the cell doesn’t match, look elsewhere.
➢Linear probing function can be given
by
• h(x, i) = (f(x) + i) mod N (i=1,2,….)

26. Figure 20.4
Linear probing
hash table after
each insertion
Data Structures & Problem Solving using JAVA/2E Mark Allen Weiss © 2002 Addison Wesley

27. Linear Probing Example
▪ Consider H(key) = key Mod 6 (assume N=6)
▪ H(11)=5, H(10)=4, H(17)=5, H(16)=4,H(23)=5
▪ Draw the Hash table
0 0 0 0 0 0
1 1 1 1 1 1
2 2 2 2 2 2
3 3 3 3 3 3
4 4 4 4 4 4
5 5 5 5 5 5

28. 28
Linear probing: Inserting a key
Idea: when there is a collision, check the next
available position in the table (i.e., probing)
h(k,i) = (h1(k) + i) mod m
i=0,1,2,...
First slot probed: h1(k)
Second slot probed: h1(k) + 1
Third slot probed: h1(k)+2, and so on
Can generate m probe sequences maximum, why?
probe sequence: < h1(k), h1(k)+1 , h1(k)+2 , ....>
wrap around

29. 29
Linear probing: Searching for a key
Three cases:
(1) Position in table is occupied with an
element of equal key
(2) Position in table is empty
(3) Position in table occupied with a
different element
Case 2: probe the next higher
index until the element is found
or an empty position is found
The process wraps around to the
beginning of the table
0
m - 1
h(k3)
h(k2) = h(k5)
h(k1)
h(k4)

30. 30
Linear probing: Deleting a key
Problems
Cannot mark the slot as empty
Impossible to retrieve keys inserted after
that slot was occupied
Solution
Mark the slot with a sentinel value DELETED
The deleted slot can later be
used for insertion
Searching will be able to find
all the keys
0
m - 1

31. Clustering Problem
• Clustering is a significant problem in linear probing. Why?
• Illustration of primary clustering in linear probing (b) versus no clustering
(a) and the less significant secondary clustering in quadratic probing(c).
Long lines represent occupied cells, and the load factor is 0.7.
Data Structures & Problem Solving using JAVA/2E Mark Allen Weiss © 2002 Addison Wesley

32. Linear Probing
▪ How about deleting items from Hash
table?
➢Item in a hash table connects to
others in the table(eg: BST).
➢Deleting items will affect finding
the others
➢“Lazy Delete” – Just mark the items
as inactive rather than removing it.

33. Lazy Delete
▪ Naïve removal can leave gaps!
Insert f
Remove e
0 a
2 b
3 c
3 e
5 d
8 j
8 u
10 g
8 s
0 a
2 b
3 c
5 d
3 f
8 j
8 u
10 g
8 s
0 a
2 b
3 c
3 e
5 d
3 f
8 j
8 u
10 g
8 s
Find f
0 a
2 b
3 c
5 d
3 f
8 j
8 u
10 g
8 s
“3 f” means search key f and hash key 3

34. Lazy Delete
▪ Clever removal
Insert f
Remove e
0 a
2 b
3 c
3 e
5 d
8 j
8 u
10 g
8 s
0 a
2b
3c
gone
5 d
3 f
8 j
8 u
10 g
8 s
0 a
2 b
3 c
3 e
5 d
3 f
8 j
8 u
10 g
8 s
Find f
0 a
2b
3c
gone
5 d
3 f
8 j
8 u
10 g
8 s
“3 f” means search key f and hash key 3

35. Load Factor (open addressing)
▪ definition: The load factor  of a probing
hash table is the fraction of the table
that is full. The load factor ranges from 0
(empty) to 1 (completely full).
▪ It is better to keep the load factor under
0.7
▪ Double the table size and rehash if load
factor gets high
▪ Cost of Hash function f(x) must be
minimized
▪ When collisions occur, linear probing can
always find an empty cell
➢But clustering can be a problem

36. Quadratic Probing

37. Quadratic probing
▪ Another open addressing method
▪ Resolve collisions by examining certain
cells (1,4,9,…) away from the original
probe point
▪ Collision policy:
➢ Define h0(k), h1(k), h2(k), h3(k), …
where hi(k) = (hash(k) + i2) mod size
▪ Caveat:
➢May not find a vacant cell!
• Table must be less than half full ( < ½)
➢(Linear probing always finds a cell.)

38. Quadratic probing
▪ Another issue
➢Suppose the table size is 16.
➢Probe offsets that will be tried:
1 mod 16 = 1
4 mod 16 = 4
9 mod 16 = 9
16 mod 16 = 0
25 mod 16 = 9 only four different values!
36 mod 16 = 4
49 mod 16 = 1
64 mod 16 = 0
81 mod 16 = 1

39. Figure 20.6
A quadratic
probing hash table
after each
insertion (note that
the table size was
poorly chosen
because it is not a
prime number).
Data Structures & Problem Solving using JAVA/2E Mark Allen Weiss © 2002 Addison Wesley

40. 40
Quadratic probing
i=0,1,2,...

41. 41
Double Hashing
(1) Use one hash function to determine the first
slot
(2) Use a second hash function to determine the
increment for the probe sequence
h(k,i) = (h1(k) + i h2(k) ) mod m, i=0,1,...
Initial probe: h1(k)
Second probe is offset by h2(k) mod m, so on ...
Advantage: avoids clustering
Disadvantage: harder to delete an element
Can generate m2 probe sequences maximum

42. 42
Double Hashing: Example
h1(k) = k mod 13
h2(k) = 1+ (k mod 11)
h(k,i) = (h1(k) + i h2(k) ) mod 13
Insert key 14:
h1(14,0) = 14 mod 13 = 1
h(14,1) = (h1(14) + h2(14)) mod
13
= (1 + 4) mod 13 = 5
h(14,2) = (h1(14) + 2 h2(14))
mod 13
= (1 + 8) mod 13 = 9
79
69
98
72
50
0
9
4
2
3
1
5
6
7
8
10
11
12
14