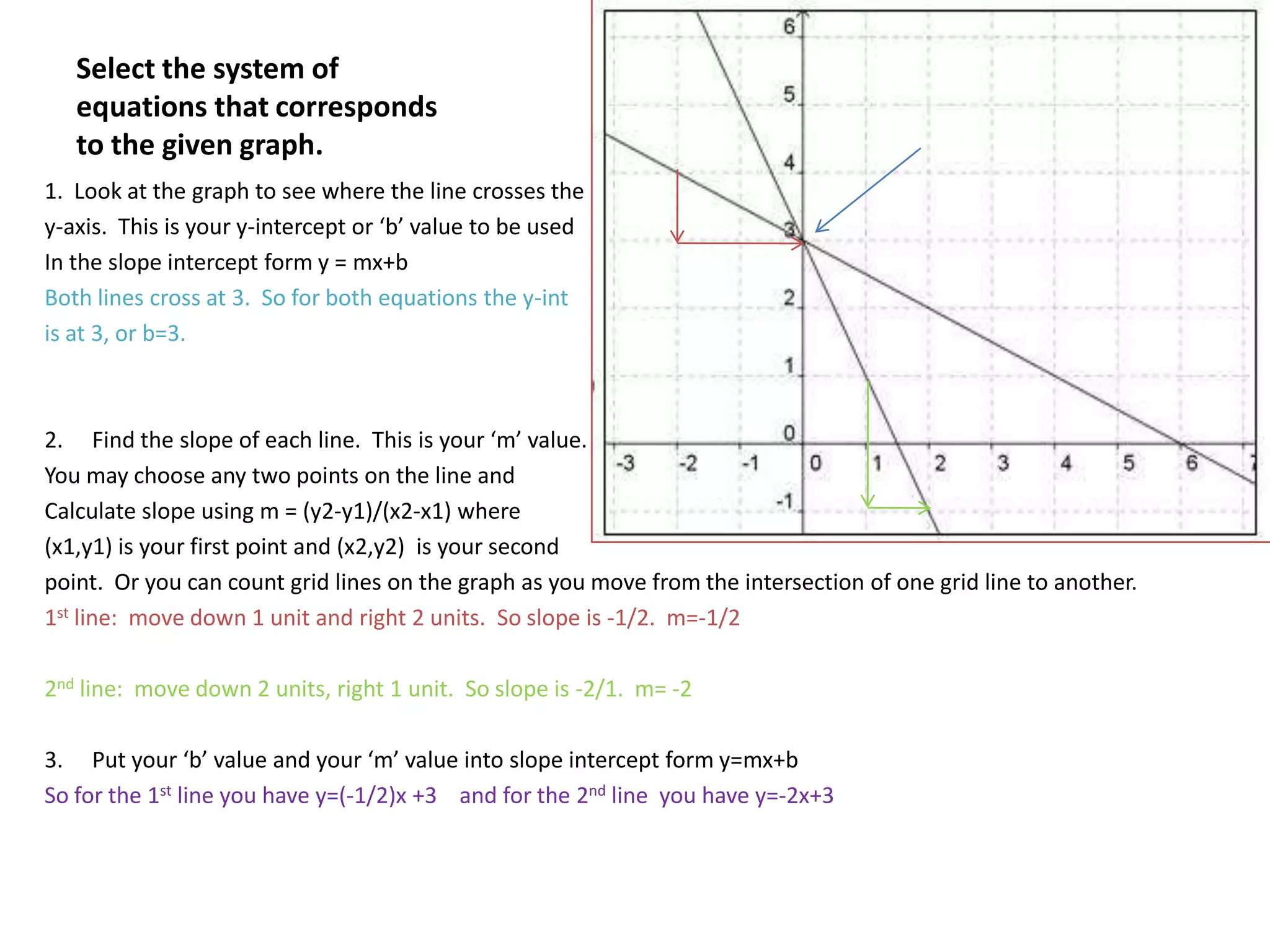
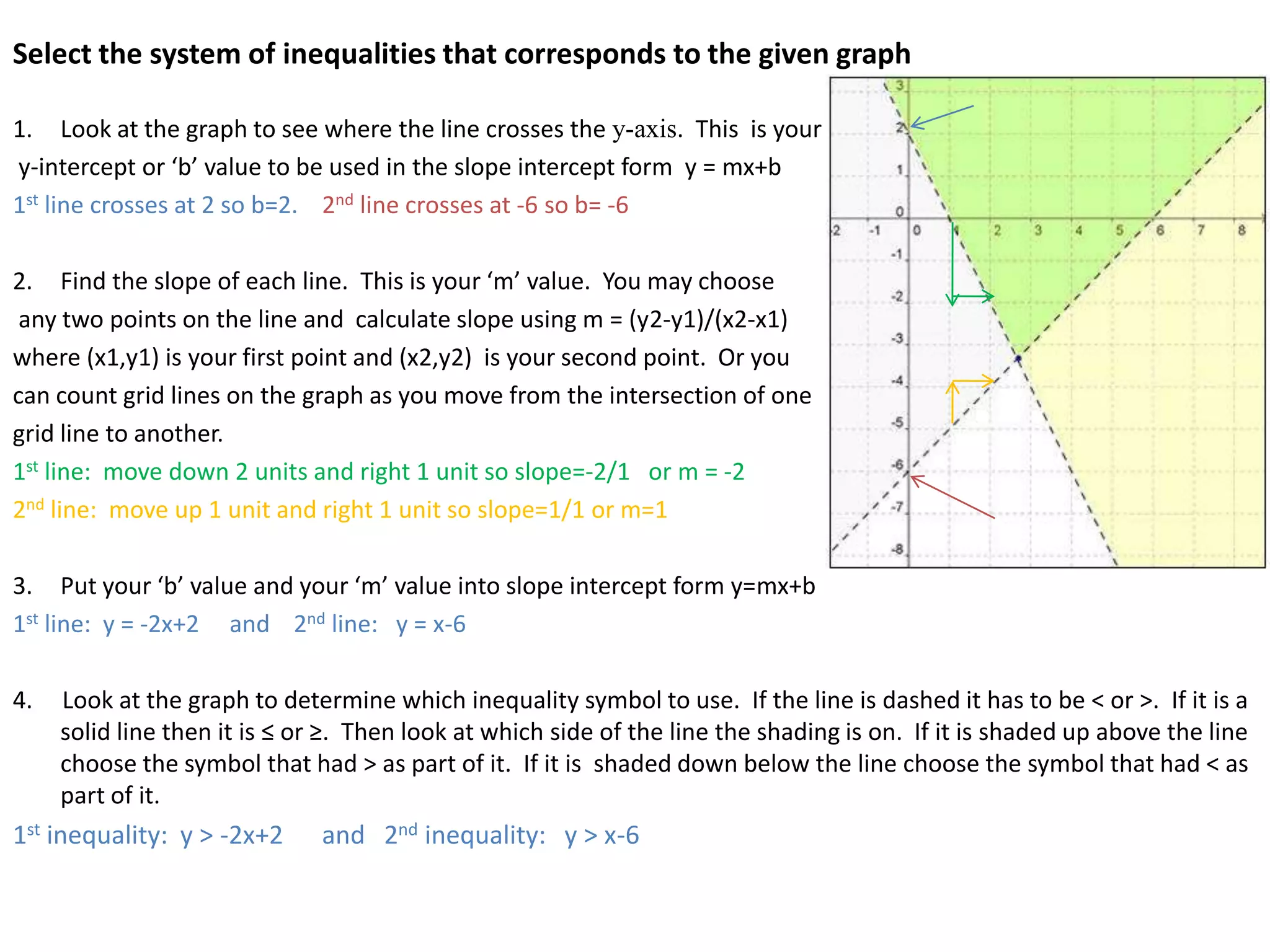
The document provides instructions for solving a system of equations based on a graph. It explains how to identify the y-intercepts and slopes of each line from the graph. It then shows how to write the equations in slope-intercept form and determine if the lines are parallel, intersecting, or overlapping based on having the same or different y-intercepts and slopes.

1. Select the system of equations that corresponds to the given graph. 1. Look at the graph to see where the line crosses they-axis. This is your y-intercept or ‘b’ value to be usedIn the slope intercept form y = mx+bBoth lines cross at 3. So for both equations the y-intis at 3, or b=3.Find the slope of each line. This is your ‘m’ value.You may choose any two points on the line and Calculate slope using m = (y2-y1)/(x2-x1) where (x1,y1) is your first point and (x2,y2) is your secondpoint. Or you can count grid lines on the graph as you move from the intersection of one grid line to another.1st line: move down 1 unit and right 2 units. So slope is -1/2. m=-1/22nd line: move down 2 units, right 1 unit. So slope is -2/1. m= -2Put your ‘b’ value and your ‘m’ value into slope intercept form y=mx+bSo for the 1st line you have y=(-1/2)x +3 and for the 2nd line you have y=-2x+3

2. Is the graph of the following system of equations parallel lines, intersecting lines, or overlapping lines? -2x + y = 3-4x + 2y = 6Solve each equation for ‘y’ so it is in slope-intercept form y = mx+bIf the equations are identical – have the same slope ‘m’ and y-intercept ‘b’ values, then they are overlapping lines.If the equations have the same slope ‘m’ value but have different y-intercept ‘b’ values, they are parallel.If neither of these are true, then the lines will intersect. -2x + y =3 add 2x to both sides -4x + 2y =6 add 4x to both sides-2x + y + 2x = 3+ 2x -4x + 2y + 4x = 6 + 4xy = 2x + 3 2y = 4x + 6 divide every term by 2 2y/2 = 4x/2 + 6/2 y = 2x +3These are the same equation.

3. For the following system, if you isolated y in the first equation to use the Substitution Method, what expression would you substitute into the second equation?2x + y = 8 Solve for y by subtracting 2x from both sides.-x – y = -5 2x + y – 2x = 8-2x y = 8 -2x or can write as y = -2x+8If asked how to solve this is what you would do next:Now substitute that into second equation (remember to use parenthesis):-x – (-2x + 8) = -5 Use distributive property to distribute the negative sign-x +2x – 8 = -5 Then combine like termsx-8 = -5 Add 8 to both sides x= 3

4. Look at the solution to the system of equations below. Was a mistake made? If so what was it?3x + y = 6x – 2y = 2y = 6 – 3xx – 2(6 – 3x) = 2x – 12 + 6x = 27x – 12 = 2 + 12 +12 x = 23(2) + y = 6 6 + y = 6–6 –6 y = 0All the math here checks out. This problem was solved correctly.

5. There are a total of 90 boys and girls who play sports. If the number of boys is 10 more than three times the number of girls, how many girls play sports at this high school?Define variables for your unknowns. Write two separate equations. One for each sentence. Let b= number of boys and g= number of girlsb+g = 90 and b=3g+10Solve one of the equations in terms of what you are trying to solve for.Solve the first equation for b by subtracting g from both sides: b = 90-g Use substitution method to solve.Remember to use parenthesis:Instead of b = 3g+10 we now have90-g = 3g+10 then add g to both sides90-g+g = 3g+10+g combine like terms90 = 4g+10 Subtract 10 from both sides90-10 = 4g+10-1080 = 4g divide both sides by 480/4 = 4g/420 =gTherefore 20 girls played sports.

6. Solve the following system of equationsy = x + 45x + y = 16Since one of the equations is already solved for ‘y’ it is easiest to use substitutionmethod. Always remember to use parenthesis when substituting. Substitute the first equation into the second equation.5x + (x+4) = 16 combine like terms6x+4 = 16 subtract 4 from both sides6x+4-4 = 16-46x = 12 divide both sides by 66x/6 = 12/6x= 2Remember to go back and substitute your solution into any of the equations and solvefor the other variable. Remember to write your final answer as an ordered pair. y= x+ 4 becomes y = (2) + 4 or y = 6Final answer is (2,6)

7. A total of 124 men and women tried out for the lead singer position. If twice the number of men less three times the number of women is equal to 28, how many women auditioned?Define variables. Write two separate equations, one for each sentence. Let m=number of men and w=number of women124 = m+w and 2m-3w=28Solve one of the equations in terms of what you are trying to solve for.Solve the first equation for m by subtracting w from both sides.124-w = m+w-w124-w = mUse substitution method to solve. Remember to use parenthesis.2m-3w=28 becomes 2(124-w) -3w = 28 Use distributive property to get 248 – 2w -3w = 28 combine like terms 248 -5w = 28 then subtract 248 from both sides 248-5w-248 = 28-248 -5w = -220 divide both sides by -5 -5w/-5 = -220/-5 w = 44 so 44 women auditioned

8. Write the equation you would use to solve the following word problem:Sasha's mom decided to get her a cell phone for her birthday. Cell Plus has a plan that costs $22.95 per month plus an additional $0.08 per minute. Cell Best has a plan that costs $27.95 per month plus an additional $0.06 per minute. How many minutes can Sasha talk and have the same cost each month?Define a variable for your unknown. Since the problem asks when the costs will be the same, set the two equations equal to each other. Let m = number of minutesCell Plus plan: 22.95+ 0.08mCell Best plan: 27.95 + 0.06mSet equal to each other since it says cost each month is the same22.95 + 0.08m = 27.95 + 0.06m then subtract 22.95 from both sides22.95 + 0.08m -22.95 = 27.95 + 0.06 – 22.950.08m = 5 + 0.06m then subtract 0.06m from both sides0.08m – 0.06m = 5 + 0.06m -0.06m0.02m = 5 divide both sides by 0.020.02m/0.02 = 5/0.02m=250

9. There were 150 people at the Junior-Senior dance. Junior tickets were $2.00 each and Senior tickets were $3.50 each. The total receipts for the dance were $405. How many Juniors bought tickets?Define variables. Write two separate equations, one for each sentence. Let j=number of juniors and Let s= number of seniorsj+s =150 and 2j + 3.5s = 405Solve one of the equations in terms of what you are trying to solve for.Solve the first equation for s by subtracting j from both sidesj+s-j = 150 –j s=150-jUse substitution method to solve.Remember to use parenthesis. 2j+3.5s = 405 becomes2j+3.5(150-j) = 405 use distributive property2j + 525 – 3.5j = 405 combine like terms-1.5j + 525 = 405 then subtract 525 from both sides-1.5j+525-525 = 405-525-1.5j = -120 divide both sides by -1.5-1.5j/-1.5 = -120/-1.5j= 80 so 80 juniors bought tickets

10. Write a set of equations that would be used to solve this word problem:An airplane flew 4.5 hours with a 45 mph head wind. The return trip with a tail wind of the same speed took 2.5 hours. Find the speed of the plane in still air.Since this problem talks about distance, rate and time, use the equation d=rtWhere the rate is the combined plane speed and wind speed. If it is a head wind, that means it is pushing against the plane slowing it down. That is why it takes more time. So r= plane speed – wind speedIf it is a tail wind, that means it is pushing with the plane speeding it up. That is why it takes less time. So r= plane speed + wind speed. Let p= speed of the planeDistance(with head wind) = (p-45)(4.5) and Distance(with tail wind) = (p+45)(2.5)If asked to solve, since the distance is the same both ways, set the equations equal to each other.(p-45)(4.5) = (p+45)(2.5) use distributive property4.5p-202.5 = 2.5p + 112.5 then subtract 2.5p from both sides4.5p – 202.5 -2.5p = 2.5p + 112.5 -2.5p2p – 202.5 = 112.5 then add 202.5 to both sides2p = 315 then divide both sides by 22p/2 = 315/2p= 157.5 mph

11. Select the system of inequalities that corresponds to the given graphLook at the graph to see where the line crosses the y-axis. This is your y-intercept or ‘b’ value to be used in the slope intercept form y = mx+b1st line crosses at 2 so b=2. 2nd line crosses at -6 so b= -6Find the slope of each line. This is your ‘m’ value. You may choose any two points on the line and calculate slope using m = (y2-y1)/(x2-x1) where (x1,y1) is your first point and (x2,y2) is your second point. Or you can count grid lines on the graph as you move from the intersection of one grid line to another.1st line: move down 2 units and right 1 unit so slope=-2/1 or m = -22nd line: move up 1 unit and right 1 unit so slope=1/1 or m=1Put your ‘b’ value and your ‘m’ value into slope intercept form y=mx+b1st line: y = -2x+2 and 2nd line: y = x-64. Look at the graph to determine which inequality symbol to use. If the line is dashed it has to be < or >. If it is a solid line then it is ≤ or ≥. Then look at which side of the line the shading is on. If it is shaded up above the line choose the symbol that had > as part of it. If it is shaded down below the line choose the symbol that had < as part of it.1st inequality: y > -2x+2 and 2nd inequality: y > x-6

12. For the following system of equations, write your own real world scenario that describes what is happening. 2x + y = 93x + 4y = 26this could be the cost of children tickets(x) and adult tickets(y)Solve the system and explain what the results mean according to your scenario.2x + y = 93x + 4y = 26Solvethe first equation for ‘y’.Subtract 2x from both sides to get y = 9-2xSubstitute that into the second equation. Remember to use parenthesis.3x+4y=26 becomes 3x+4(9-2x) = 26 use distributive property 3x + 36 – 8x = 26 combine like terms -5x + 36 = 26 subtract 36 from both sides -5x+36-36 = 26-36 -5x = -10 divide both sides by -5 -5x/-5 = -10/-5 x = 2Remember to go back and substitute your solution into any of the equations and solve for the other variable. Remember to write your final answer as an ordered pair. Now y=9-2x becomes y = 9-2(2) or y = 9-4 or y=5Solution is (2,5) or the price of a child ticket is $2.00 and price of an adult ticket is $5.00

13. Your piggy bank has a total of 47 coins in it; some are dimes and some are nickels. If you have a total of $3.95, how many nickels and how many dimes do you have?Define variables for your unknowns. Write two separate equations, one for each sentence.The first one will be about the number of coins. The second will be about the dollar valueworth of the coins. Let d= number of dimes. Let n= number of nickelsd+n = 47 and since a dime is worth $0.10 and a nickel is worth $0.05 you have 0.10d+0.05n=3.95Solve the first equation for one of the variables. Then substitute that into the secondequation. Remember to use parenthesis.Solve first equation for n by subtracting d from both sides:n=47-dSo 0.10d+0.05n=3.95 becomes 0.10d + 0.05(47-d)= 3.95 use distributive property to get 0.10d +2.35 – 0.05d = 3.95 combine like terms 0.05d +2.35 = 3.95 then subtract 2.35 from both sides 0.05d + 2.35 -2.35 = 3.95-2.35 0.05d = 1.60 divide both sides by 0.05 0.05d/0.05 = 1.60/0.05 d = 32Remember to go back and substitute your solution into any of the equations and solve forthe other variable.n=47-d becomes n=47-32 so n=15. There were 32 dimes and 15 nickels.

14. Solve the following system of equations:x – y = 10x + y = 8Since the coefficients of the ‘y’ variables in both equations are 1 and -1, we can solve byusing elimination method. Add the two equations together to solve. x – y = 10+ x + y =8------------------------ 2x + 0 = 18 or 2x =18 then divide both sides by 2 2x/2 = 18/2 x = 9Remember to go back and substitute your solution into any of the equations and solvefor the other variable. Remember to write your final answer as an ordered pair. Now x + y =8 becomes (9)+y =8 subtract 9 from both sides 9 + y -9 = 8-9 y = -1Solution is (9,-1)