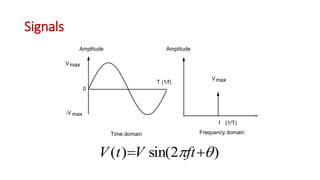
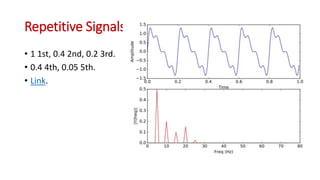
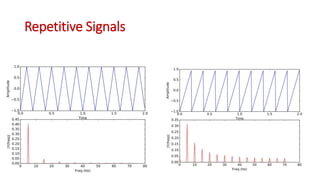
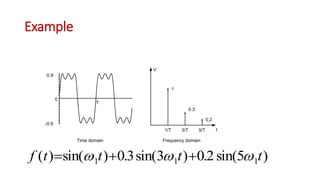
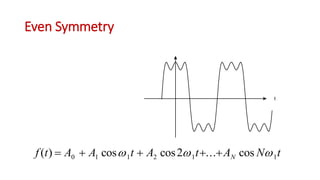
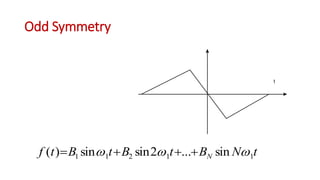
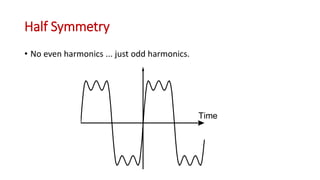
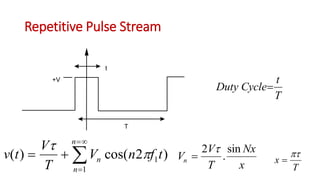
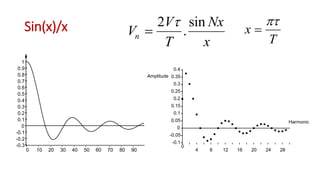
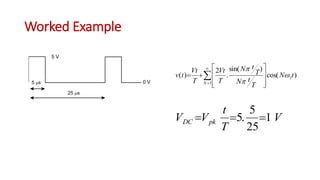
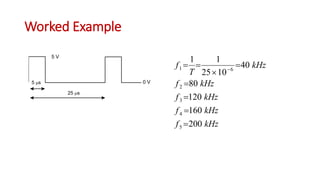
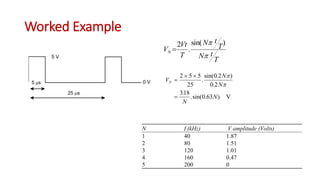
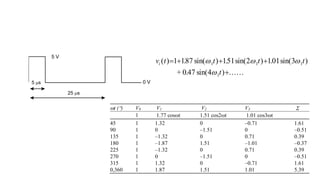
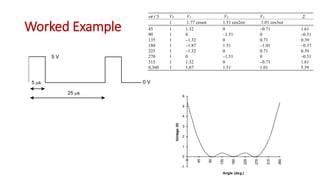
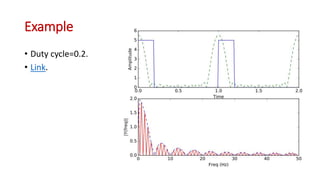
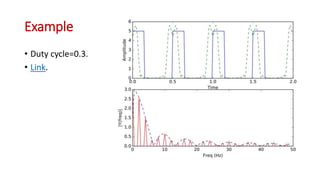
This document discusses the analysis of digital pulses in both the time and frequency domains. It begins by introducing signals and repetitive signals, describing their representations in both domains. It then discusses repetitive pulse streams and their Fourier series representations. Specific topics covered include duty cycle, the sine function divided by x, even symmetry, odd symmetry, and half symmetry. Worked examples are provided to demonstrate analyzing a pulse stream and calculating its harmonic amplitudes. The document concludes with examples of different duty cycle pulse streams.

1. CSN08704
Data, Audio, Video and Images
http://asecuritysite.com/comms
Telecommunications
Prof Bill Buchanan
4. Analysis of Digital Pulses

2. CSN08704
Data, Audio, Video and Images
http://asecuritysite.com/comms
Telecommunications
Prof Bill Buchanan
4. Analysis of Digital Pulses: Frequency
and Time Domain

3. Signals
V t V ft( ) sin( ) 2 
Time domain Frequency domain
Vmax
f
T (1/f)
(1/T)
-V max
0
Vmax
AmplitudeAmplitude

4. Repetitive Signals
ω1 = 2.π.f1 where f1 is the fundamental frequency.
tNBtBtB
tNAtAtAAtf
N
N
11211
112110
sin...2sinsin
cos...2coscos)(





5. Repetitive Signals
• 1 1st, 0.4 2nd, 0.2 3rd.
• 0.4 4th, 0.05 5th.
• Link.

6. Repetitive Signals

7. Example
1
0.3
0.2
1/T 3/T 5/T f
T
0.9
-0.9
0
Time domain Frequency domain
V
f t t t t( ) sin( ) . sin( ) . sin( )    1 1 103 3 02 5

8. Even Symmetry
t
f t A A t A t A N tN( ) cos cos ... cos    0 1 1 2 1 12  

9. Odd Symmetry
t
f t B t B t B N tN( ) sin sin ... sin   1 1 2 1 12  

10. Half Symmetry
• No even harmonics ... just odd harmonics.
Time

11. CSN08704
Data, Audio, Video and Images
http://asecuritysite.com/comms
Telecommunications
Prof Bill Buchanan
4. Analysis of Digital Pulses: Pulse
Analysis

12. Repetitive Pulse Stream
t
+V
T
Duty Cycle
t
T

v t
V
T
V n f tn
n
n
( ) cos( ) 




2 1
1
V
V
T
Nx
x
n 
2 
.
sin
x
T



13. Sin(x)/x
0 10 20 30 40 50 60 70 80 90
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
-0.1
-0.2
-0.3
V
V
T
Nx
x
n 
2 
.
sin
x
T


0
4 8 12 16 20 24 28
Harmonic
Amplitude
0.4
0.35
0.3
0.25
0.2
0.15
0.1
0.05
0
-0.05
-0.1

14. Worked Example
5 V
0 V
25 s
5 s
v t
Vt
T
Vt
T
N t
T
N t
T
N t
N
( ) .
sin( )
cos( ) 










2
1
1



V V
t
T
VDC pk  5
5
25
1.

15. Worked Example
f
T
kHz
f kHz
f kHz
f kHz
f kHz
1 6
2
3
4
5
1 1
25 10
40
80
120
160
200
 







5 V
0 V
25 s
5 s

16. Worked Example
5 V
0 V
25 s
5 s
V
Vt
T
N t
T
N t
T
N 
2
.
sin( )

V
N
N
N
N
N 
 

2 5 5
25
0 2
0 2
318
0 63
.
sin( . )
.
.
.sin( . )


V
N f (kHz) V amplitude (Volts)
1
2
3
4
5
40
80
120
160
200
1.87
1.51
1.01
0.47
0

17. 5 V
0 V
25 s
5 s
v t t t t
t
i ( ) . sin( ) . sin( ) . sin( )
. sin( ) ......
   

1 187 151 2 101 3
0 47 4
1 1 1
1
  
+
t () V0 V1 V2 V3 
1 1.77 cost 1.51 cos2t 1.01 cos3t
45 1 1.32 0 –0.71 1.61
90 1 0 –1.51 0 –0.51
135 1 –1.32 0 0.71 0.39
180 1 –1.87 1.51 –1.01 –0.37
225 1 –1.32 0 0.71 0.39
270 1 0 –1.51 0 –0.51
315 1 1.32 0 –0.71 1.61
0,360 1 1.87 1.51 1.01 5.39

18. Worked Example
-1
0
1
2
3
4
5
6
0
45
90
135
180
225
270
315
360
Angle (deg.)
Voltage(V)
t () V0 V1 V2 V3 
1 1.77 cost 1.51 cos2t 1.01 cos3t
45 1 1.32 0 –0.71 1.61
90 1 0 –1.51 0 –0.51
135 1 –1.32 0 0.71 0.39
180 1 –1.87 1.51 –1.01 –0.37
225 1 –1.32 0 0.71 0.39
270 1 0 –1.51 0 –0.51
315 1 1.32 0 –0.71 1.61
0,360 1 1.87 1.51 1.01 5.39
5 V
0 V
25 s
5 s

19. Example
• Duty cycle=0.2.
• Link.

20. Example
• Duty cycle=0.3.
• Link.

21. CSN08704
Data, Audio, Video and Images
http://asecuritysite.com/comms
Telecommunications
Prof Bill Buchanan
4. Analysis of Digital Pulses