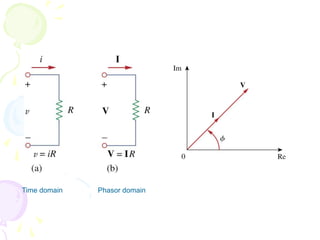
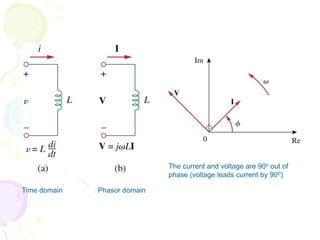
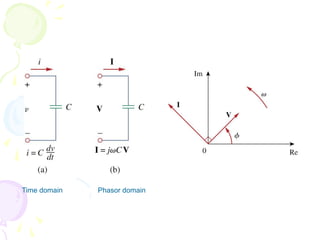
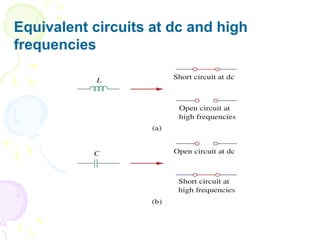
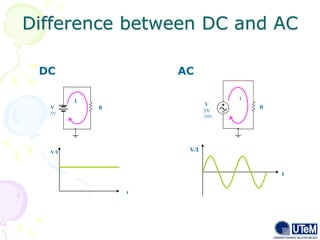
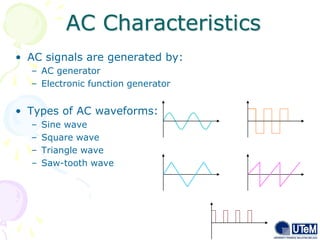
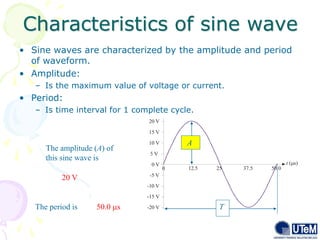
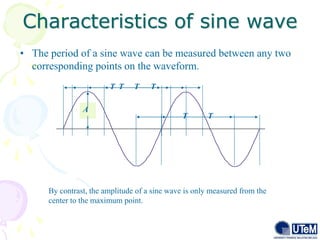
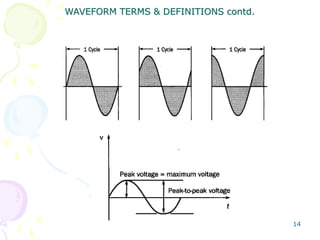
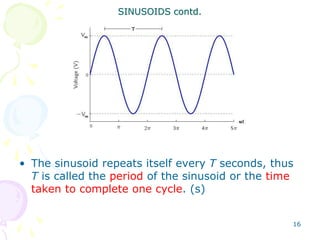
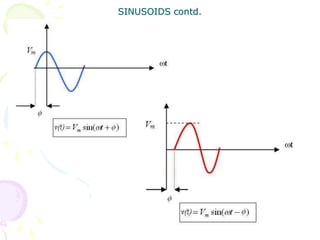
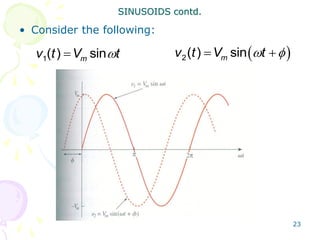
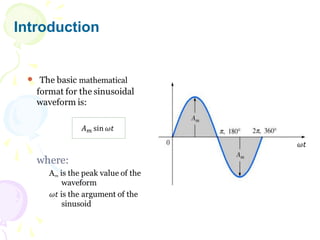
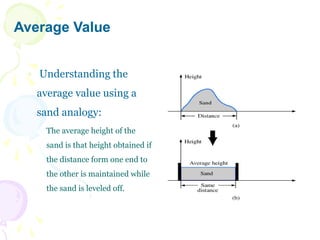
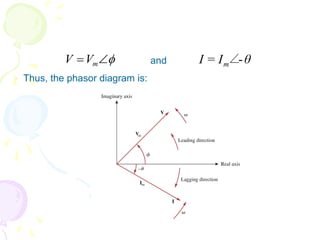
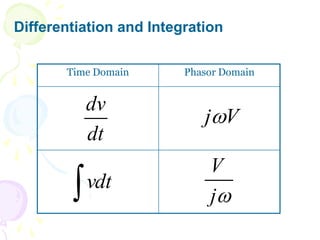
This document discusses alternating current (AC) sources and characteristics. It begins by defining AC as an electrical current whose magnitude and direction vary sinusoidally over time. Common AC waveforms include sine, square, triangle, and sawtooth waves. The sine wave is considered the fundamental AC waveform and is characterized by its amplitude and period. Other key concepts covered include frequency, phase, average and effective (RMS) values, and using phasors to represent sinusoidal waveforms in the frequency domain.

1. BEKG 1123
PRINCIPLES OF ELECTRIC &
ELECTRONICS

2. 2
CHAPTER 3:
AC Sources
and
AC Characteristic

3. AC Source
Learning Outcome
• In this part, we will cover on:
4.1 Waveform type
4.2 AC characteristic
3

4. 4
• AC is an electrical current whose magnitude and
direction vary sinusoidally with time.
• Such as current reverses at regular time intervals
and has alternately positive and negative values.
INTRODUCTION

5. 5
• The circuits analysis is considering the time-
varying voltage source or current source.
• Circuits driven by sinusoidal current or voltage
sources are called ac circuits.
• A sinusoid can be express in either sine or
cosine form.
INTRODUCTION..cont

6. Difference between DC and AC
DC AC
6
V
5V
1kHz
R
I
V/I
t
V
5V
I
R
V/I
t

7. AC Characteristics
7
• AC signals are generated by:
– AC generator
– Electronic function generator
• Types of AC waveforms:
– Sine wave
– Square wave
– Triangle wave
– Saw-tooth wave

8. Characteristics of sine wave
8
• The sinusoidal waveform (sine wave) is the fundamental of
AC current and AC voltage waveform.

9. Characteristics of sine wave
9
• Sine waves are characterized by the amplitude and period
of waveform.
• Amplitude:
– Is the maximum value of voltage or current.
• Period:
– Is time interval for 1 complete cycle.
0 V
10 V
-10 V
15 V
-15 V
-20 V
t ( s)

0 25 37.5 50.0
20 V
The amplitude (A) of
this sine wave is
20 V
The period is 50.0 s
A
T

10. Characteristics of sine wave
10
• The period of a sine wave can be measured between any two
corresponding points on the waveform.
T T T T
T T
A
By contrast, the amplitude of a sine wave is only measured from the
center to the maximum point.

11. Characteristics of sine wave
11
• Frequency:
– Frequency ( f ) is the number of cycles that a sine wave completes in
one second.
– Frequency is measured in hertz (Hz).
• Example:
3.0 Hz
If 3 cycles of a wave occur in one second, the frequency is
1.0 s

12. Characteristics of sine wave
12
• Relationship between period and frequency
– The period and frequency are reciprocals of each other.
– Frequency = 1/ time for 1 complete cycle
• Examples:
– If the period is 50 s, what is the frequency?
– If frequency is 60Hz, what is the period?
and
f
T
1

T
f
1


13. 13
Waveform Terms &
Definitions
Definitions:
Period – the time taken to complete a cycle, T (s)
Peak value – the maximum instantaneous value measured from its zero value, Vp @
Vm (V)
Peak-to-peak value – the maximum variation between the maximum positive
instantaneous value and the maximum negative value, Vp-p (V)
Instantaneous voltage / current - has a value that corresponds to a specific time t.
Every waveform has an infinity number of instantaneous values. Such a waveform
is described as the parameter as a function of time. In the case of a voltage it will
be written as v(t).
Cycle – the portion of a waveform contained in one period of time. For a sine wave,
it is the complete event starting with a rise from zero energy to a maximum
amplitude, its return to zero, the rise to a maximum in the opposite direction, and
then its return to zero.

14. 14
WAVEFORM TERMS & DEFINITIONS contd.

15. 15
Sinusoids
• Consider the expression of a sinusoidal voltage
where


( ) sin
m
v t V t


= the amplitude of the sinusoid
= the angular frequency in radians/s
= the argument of the sinusoid
m
V
t

16. 16
• The sinusoid repeats itself every T seconds, thus
T is called the period of the sinusoid or the time
taken to complete one cycle. (s)
SINUSOIDS contd.

17. 17
• The number of cycles per second is called
frequency, f. (Hz)
• Angular frequency, ω. (rad/s)
• An important value of the sinusoidal function is
its RMS (root-mean-square) value.
SINUSOIDS contd.
1
f
T

2 f
 

 
2
m
RMS dc
V
V V

18. 18
• Note: Radian measure
– ω is usually expressed in radian/s
– 2 radians = 360
– to convert from degrees to radians, multiply by /180.
– to convert from radians to degrees, multiply by 180/.
• From the general expression of the sinusoidal
voltage, we can find the value of voltage at any
given instant of time.
SINUSOIDS contd.

19. 19
• If the waveform does not pass through zero at
t=0, it has a phase shift.
• For a waveform shifted left,
• For waveform shifted right,
where
 
 
 
( ) sin
m
v t V t
 = phase angle of the sinusoid function
SINUSOIDS contd.
 
 
 
( ) sin
m
v t V t

20. 20
SINUSOIDS contd.

21. 21
Example:
1. Find the amplitude, phase, period and
frequency of the sinusoid
Solution:
Amplitude, Vm = 12V
Phase, = 10˚
Angular frequency, ω = 50rad/s
thus the period, T =
The frequency, f =
SINUSOIDS contd.

2 2
50
0.1257s
 

 
7.958
1
z
T
H

 
  
( ) 12sin 50 10
v t t

22. 22
2. A sinusoidal voltage is given by the expression
V = 300 cos (120t + 30).
a) What is the frequency in Hz?
b) What is the period of the voltage in miliseconds?
c) What is the magnitude of V at t = 2.778ms?
d) What is the RMS value of V?
Solution:
a) Given ω = 120 = 2f, thus f = 60Hz
b) T = 1/f = 16.67ms
c) V = V = 300 cos (120x2.778m + 30)
= 300 cos (60 + 30) = 0V
d) Vrms = 300/√2 = 212.13V
SINUSOIDS contd.

23. 23
• Consider the following:
SINUSOIDS contd.
1( ) sin
m
v t V t

  
2( ) sin
m
v t V t
 
 

24. 24
• The v2 is occurred first in time.
• Thus it can be said that v2 leads v1 by or v1
lags v2 by .
• If ≠ 0 we can say v1 and v2 are out of phase.
• If = 0 we can say v1 and v2 are in phase.
• v1 and v2 can be compared in this manner
because they operate at the same frequency (do
not need to have the same amplitude).
SINUSOIDS contd.





25. 25
• Transformation between cosine and sine form
Converting from negative to positive magnitude
where
SINUSOIDS contd.
sin cos( 90 )
cos sin( 90 )
A A
A A
  
  
sin sin( 180 )
cos cos( 180 )
A A
A A
   
   
A t
 
 

26. 26
Example:
1. For the following sinusoidal voltage, find the
value v at t = 0s and t = 0.5s.
v = 6 cos (100t + 60˚)
Solution:
Note: both ωt and must be in same unit before adding them up.
SINUSOIDS contd.
at t = 0.5s
v = 6 cos (50 rad +60˚)
= 4.26V
at t = 0s
v = 6 cos (0+60˚)
= 3V


27. 27
2. Calculate the phase angle between
v1 = -10 cos (ωt + 50)
v2 = 12 sin (ωt - 10)
State which sinusoid is leading.
Solution:
In order to compare v1 and v2, we must express them in
the same form (either in cosine or sine function) with
positive magnitude. Note: the value of must be
between 0 to 180
v1 = -10 cos (ωt + 50) = 10 cos (ωt + 50 - 180)
= 10 cos (ωt - 130)
SINUSOIDS contd.


28. 28
and
v2 = 12 sin (ωt - 10) = 12 cos (ωt - 10 - 90)
= 12 cos (ωt - 100)
the equation v2 can be written in the following form
v2 = 12 cos (ωt - 130 + 30)
‘+30’ in the above expression means v2 leads v1 by 30
SINUSOIDS contd.

29. AC Charateristic
Learning Outcomes
At the end of this part, students should be able to;
1. identify a sinusoidal waveform and measure
its characteristics.
2. apply phasor to analyze alternating signals.
3. use a phasor to represent a sine wave.

30. Introduction
 A sinusoid is a signal that has the form of the sine or cosine
function.
 A sinusoidal current is usually referred to as alternating
current (ac).
 Such a current reverses at regular time intervals and has
alternately positive and negative values.
 AC circuits are the circuits driven by sinusoidal current or
voltage sources.

31. Introduction

32. Introduction

33. Average Value
 Understanding the
average value using a
sand analogy:
 The average height of the
sand is that height obtained if
the distance form one end to
the other is maintained while
the sand is leveled off.

34. Average Value (cont)
The algebraic sum of the areas must be determined, since some area
contributions will be from below the horizontal axis.
Area above the axis is assigned a positive sign and area below the axis is
assigned a negative sign.
The average value of any current or voltage is the value indicated on a
dc meter – over a complete cycle the average value is the equivalent dc
value.

35. Effective (RMS) Value
 Effective value arises from the need to measure the effectiveness of
the voltage or current source in delivering the power to resistive load.
 Definition: Effective value of periodic current is the dc current that
delivers the same average power to a resistor as the periodic current.
 Effective value is given by ,
 This indicates that effective value is the square root of the
average of the square of the periodic signal.
dt
v
T
V
T
eff 

0
2
1
dt
i
T
I
T
eff 

0
2
1

36. Effective (RMS) Value (cont)
 For the sinusoid the effective or rms
value is
 Similarly for





T
m
T
m
rms
dt
t
T
I
tdt
I
T
I
0
2
0
2
2
)
2
cos
1
(
2
1
cos
1


2
m
rms
I
I 
,
cos
)
( t
V
t
v m 

2
m
rms
V
V 
,
cos
)
( t
I
t
i m 


37. Phasors
 Sinusoids are easily expressed in terms of phasors.
 A phasor is a complex number that represents the amplitude
and phase of the sinusoid.
 Complex number can be written in one of the following three
forms:
a. Rectangular form:
b. Polar form:
c. Exponential form:
jy
x
z 



 r
z

j
re
z 

38.  where:
j =
x = real part of z
y = imaginary part of z
r = the magnitude of z
ϕ = the phase of z
1


39. Relationship between Rectangular and
Polar Form
2 2 1
; tan
y
r x y
x
 
  
cos ; sin
x r y r
 
 
 
  
     
cos sin
z x jy r r j r
or
Thus, z may be written as,
Note: addition and subtraction of complex number better perform in rectangular form.
Multiplication and division in polar form.

40. Basic Properties of Complex Numbers
Addition :
Subtraction :
Multiplication :
Division :
2
1
2
1
2
1 
 

 r
r
z
z
2
1
2
1
2
1

 


r
r
z
z
   
2
1
2
1
2
1 y
y
j
x
x
z
z 




   
2
1
2
1
2
1 y
y
j
x
x
z
z 





41. Reciprocal :
Square Root :
Complex Conjugate :
note:
In general,




r
z
1
1
 
2
/


 r
z
  
 j
re
r
jy
x
z 







j
j


1


 sin
j
cos
e j




42.  As we know, the sinusoidal voltage can be represented in sine
or cosine function.
 First, consider the cosine function as in:
 This expression is in time domain.
 In phasor method, we no longer consider in time domain instead
in phasor domain (also known as frequency domain).
 
( ) cos
m
v t V t
 
 

43.  The cosine function will be represented in phasor and complex
number such as:
 For example:
Transform the sinusoid:
v(t) = 12 cos (377t - 60˚)
thus,
 
 
( ) cos
cos sin
m
m
m m
v t V t
V
V j V
 

 
 
 
 
39
.
10
6
60
12 j
v 



 or

44.  The phasor representation carries only the amplitude and phase
angle information.
 The frequency term is dropped since we know that the
frequency of the sinusoidal response is the same as the source.
 The cosine expression is also dropped since we know that the
response and source are both sinusoidal.

45. Sinusoid-phasor Transformation
Time-domain representation Phasor-domain Representation
 
   
 
   
cos
sin 90
cos I
sin I 90
m m
m m
m m
m m
V t V
V t V
I t
I t
  
  
  
  
  
    
  
    
* to get the phasor representation of a sinusoid, we express it in cosine form.

46. and
 Thus, the phasor diagram is:


 m
V
V θ
I
I m -
∠
=

47. Differentiation and Integration
Time Domain Phasor Domain
dt
dv
V
j
vdt

j
V

48. Example 1
Evaluate the following complex numbers:
o
o
o
j
j
b
j
j
a
30
10
)]
4
3
/(
)
40
3
5
10
.[(
*
]
60
5
)
4
1
)(
2
5
.[(













49. Example 1:Solution
   
   
 
   
 
 
67
13
5
15
67
13
5
15
33
4
5
2
18
13
60
60
5
18
13
60
5
4
1
2
5
.
j
.
.
j
.
.
j
.
j
sin
j
cos
j
j
j
*
*
*
*
o






























(a) Using polar-rectangular transformation, addition and subtraction,
(b) Using calculator,
2
.
2
293
.
8 j



50. Example 2
Transform these sinusoids to phasors:
 V
t
v
b
A
t
i
a







50
30
sin
4
)
(
)
40
50
cos(
6
)
(

51. Example 2: Solution
Refer to sinusoids to phasors transformation table:
a)
b) Since
so
A
40
6
I 



 
   
 V
140
t
30
cos
4
90
50
t
30
cos
4
50
t
30
sin
4
v
90
A
cos
A
sin
















V
140
4
V 



52. Example 3
Given y1 = 20 cos (100t - 30) and y2 = 40 cos (100t + 60). Express
y1 + y2 as a single cosine function.
Solution:
In phasor form
Thus, y1 + y2 = 44.72 cos (100t + 33.4)

























4
.
33
72
.
44
64
.
24
32
.
37
64
.
34
20
10
32
.
17
60
40
30
20
60
40
&
30
20
2
1
2
1
j
j
j
y
y
y
y

53. Circuit Elements in Phasor Domain
 Circuit analysis is much simpler if it is done in phasor domain.
 In order to perform the phasor domain analysis, we need to
transform all circuit elements to its phasor equivalent.
 Transform the voltage-current relationship from time domain to
the frequency domain for each element.

54. Phasor Relationships for Resistor
 If current through resistor is:
 The voltage across R is V=IR (Ohm’s Law); in phasor form:
 But; phasor representation of the current is:
 Hence: V=RI







m
m
I
I
t
I
i )
cos(


 m
RI
V


m
I
I =
Phasor domain
Ohm’s Law in phasor form

55. Time domain Phasor domain

56. Phasor Relationships for Inductor
 If current through inductor is:
 The voltage across the inductor:
 Which transforms to the phasor
 But
 Hence


m
I
I =
)
t
cos(
LI
)
t
sin(
LI
dt
di
L
v m
m 






 90






90


 
 m
LI
V
)
cos( 
 
 t
I
i m
LI
j
LI
j
V m 

 



57. Time domain Phasor domain
The current and voltage are 90o out of
phase (voltage leads current by 90o)

58. Phasor Relationships for Capacitor
 Given voltage through capacitor is:
 The current through capacitor is:
 But
 Thus: where
 And
)
cos( 
 
 t
V
v m
dt
dv
C
i 
)
90
cos(
)
sin( 




 




 t
CV
t
CV
i m
m
90


 
 m
CV
I
90
1

j
CV
j
CV
j
I m 

 

 

m
V
)
/( C
j
I
V 


59. Time domain Phasor domain

60. Voltage – Current Relationships
Element Time domain
Frequency domain
R
L
C
Ri
v 
dt
di
L
v 
dt
dv
C
i 
RI
V 
LI
j
V 

C
j
I
V



61. Example 4
a) If voltage v = 10 cos (100t + 30⁰) is applied to a 50μF capacitor,
calculate the current through the capacitor.
b) What is the voltage across a 2μF capacitor when the current
through it is i = 4 sin (106t + 25⁰) A?
Ans:
a) 50 cos (100t + 120⁰) mA
b) 2 sin (106t - 65⁰) V

62. Impedance
 Previously:
 In terms of the ratio of the phasor voltage to the phasor current:
 Ohm’s Law in phasor form for any type of element
C
j
I
V
,
LI
j
V
,
RI
V

 


C
j
I
V
L
j
I
V
R
I
V


1
,
, 


ZI
V
or
,
I
V
Z 


63. Impedances and Admittances of Passive
Elements
Element Impedance
Admittance
R
L
C
R
Z
L
j
Z 

C
j
1
Z


R
1
Y 
L
j
1
Y


C
j
Y 


64. Equivalent circuits at dc and high
frequencies

65. Impedance in Rectangular Form
 The impedance may be expressed in rectangular form as
 where R = Re Z is the resistance and X = Im Z is the reactance.
 The impedance is inductive when X is positive or capacitive
when X is negative.
 The impedance may be also be expressed in polar form as
jX
R
Z 



 Z
Z

66.  where
 and




 Z
jX
R
Z
R
X
tan
,
X
R
Z 1
2
2 


 

 sin
Z
X
,
cos
Z
R 


67. Impedance Combinations
 Consider the N series-connected
impedances shown in figure.
 The same current I flows through
the impedances.
 Applying KVL around the loop gives
 The equivalent impedance at the input terminals is
or
)
Z
...
Z
Z
(
I
V
...
V
V
V N
2
1
N
2
1 +
+
+
=
+
+
+
=
N
2
1
eq Z
...
Z
Z
I
V
Z +
+
+
=
= N
2
1
eq Z
...
Z
Z
Z +
+
+
=

68. Voltage Divider of Series Circuit
 If N = 2, the current through the
impedances is
 Since V1 = Z1I and V2 = Z2I ,
then:
2
1 Z
Z
V
I
+
=
V
Z
Z
Z
V
,
V
Z
Z
Z
V
2
1
2
2
2
1
1
1
+
=
+
=

69. Parallel Circuit
 We can obtain the equivalent impedance or admittance of the N
parallel-connected impedances shown in figure.
 The cross voltage each impedance is the same.

70. Parallel Circuit
 Applying KCL at the top node
 The equivalent impedance is
 And the equivalent admittance is
N
2
1
eq
Z
1
...
Z
1
Z
1
V
1
Z
1





N
2
1
eq
Y
....
Y
Y
Y 



)
Z
1
...
Z
1
Z
1
(
V
I
...
I
I
I
N
2
1
N
2
1









71. Current Divider of Parallel Circuit
 Eg: When N = 2, as shown in Figure
5.19, the equivalent impedance
becomes
 since V = IZeq=I1Z1=I2Z2 the currents
in the impedances are
2
1
2
1
2
1
2
1
eq
eq
Z
Z
Z
Z
Z
/
1
Z
/
1
1
Y
Y
1
Y
1
Z







I
Z
Z
Z
I
,
I
Z
Z
Z
I
2
1
1
2
2
1
2
1





72. Example 5
Find the input impedance of the circuit in figure below. Assume that
the circuit operates at =50rad/s.

73. Example 6
Find Zeq in the circuit.
Ans: Zeq = 1 + j0.5 Ω

74. Example 7
Find v(t) and i(t) in the circuit of Figure below.

5
0.1F
+
v
-
Vs = 10 cos 4t
i

75. Example 7: Solution
vs =10 cos 4t → Vs =
The impedance is
Hence the current
V
0
10 



5
.
2
j
5
1
.
0
4
j
1
5
C
j
1
5
Z 






A
57
.
26
789
.
1
8
.
0
j
6
.
1
5
.
2
j
5
0
10
Z
V
I s











76. Example 7: Solution cont
Hence the voltage across the capacitor
Converting I and V to the time domain,
V
j
C
j
I
IZ
V C 








 43
.
63
47
.
4
1
.
0
4
57
.
26
789
.
1

   
   V
43
.
63
t
4
cos
47
.
4
t
v
A
57
.
26
t
4
cos
789
.
1
t
i







77. Example 8
Determine v(t) and i(t).
+
v
-
+
-
4Ω
i
0.2H
vs = 20 sin (10t + 30⁰) V
Ans: i(t) = 4.472 cos (4t+3.43⁰) A
v(t) = 8.944 cos (4t+93.43⁰) V

78. Chapter Summary