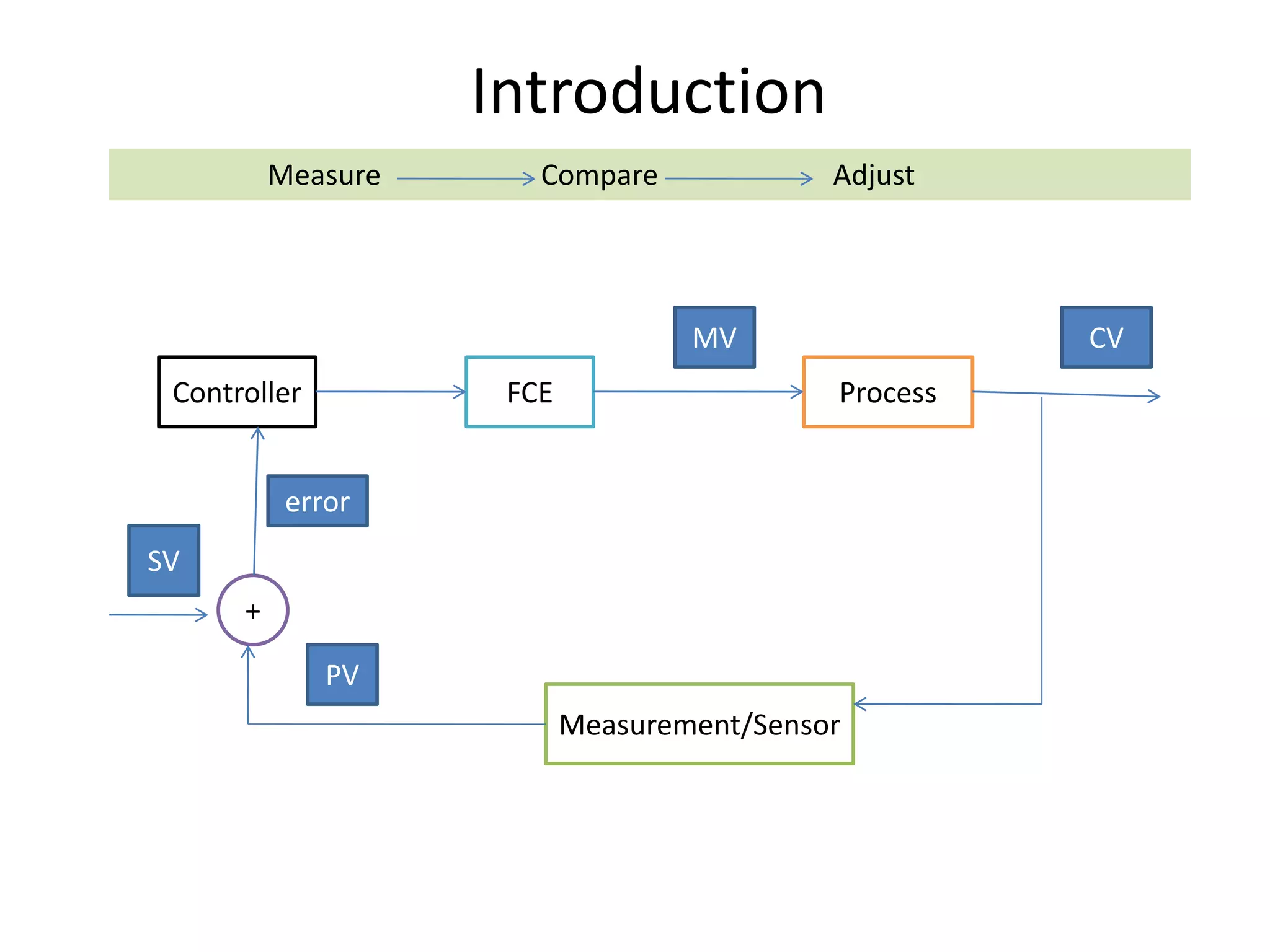
This document provides an introduction to process control and dynamics laboratory experiments. It discusses key process control concepts like feedback control loops, controllers, sensors, setpoints, process values, and manipulated variables. The laboratory experiments will focus on controlling processes like gas pressure, level and flow, temperature, and pH using different control methods including open loop, P-control, PI control, and PID control. Students will learn to understand control systems, illustrate instrumentation, analyze controller responses, tune controllers to find optimal PID settings, and use the Ziegler-Nichols method to determine PID values from open loop tests. System behaviors like underdamped, critically damped, and overdamped responses will also be explored.

1. Briefing on Process Control and
Dynamics Laboratory
20 January 2010

2. Introduction
Process
Controller FCE
Measurement/Sensor
+
error
SV
PV
MV CV
Measure Compare Adjust

3. PV = Process Value/Controlled Variable
SV = Setpoint/Desired Value
MV = Manipulated Value/Controller Output
Error = Deviation
Objective : To bring PV = SV by manipulating FCE(Final
Control Element) via MV

4. Upset / Disturbance
Setpoint change : at the SV
Load Variables : all other variables that cause upset and affect control (e.g: input
fow rate, output flow rate, environment, heater power variation
Control is easier( unnecessary) if there is no UPSET
Control is more difficult if UPSET is due to LOAD upset than setpoint
upset.

5. Laboratory
Experiment 1: Gas Pressure Control
Experiment 2: Level Flow Control
Experiment 3: Flow Control
Experiment 4: On Off & Temperature Control
Experiment 5: pH Control using Open Loop
Method
Experiment 6: pH Control using Closed Loop
Method

6. What is expected from you ?
1. Understand the feedback control loop system
2. Able to illustrate control system
instrumentation (transducer,transmitter, FCE
etc.)
3. Able to analyze responses at different value of
PID
4. Tuning- Find the best PID for the process
5. Find PID using open loop method
(Ziegler and Nichols Formula)

7. What you will see in the lab?
• PID , where:
• PB = 100/Kc ; TI= time integral ; TD = time
derivative
• P-control only
• PI control
• PID

8. System Behavior
Underdamped
An underdamped response is one that
oscillates within a decaying envelope.
The more underdamped the system,
the more oscillations and longer it
takes to reach steady-state. Here
Damping Ratio is always < 1
Critically damped
A critically damped response is the
response that reaches the steady-state
value the fastest without being
underdamped. It is related to critical
points in the sense that it straddles
the boundary of underdamped and
overdamped responses. Here,
damping ratio is always less than or
equal to one (≤1) . There should be no
oscillation about the steady state
value in the ideal case.
Overdamped
An overdamped response is the
response that does not oscillate about
the steady-state value but takes longer
to reach than the critically damped
case. Here Damping Ratio is >1

9. Ziegler and Nichols formula
• Please refer to the handout given.

10. Laboratory Report
• Introduction/Theory of the experiment
• Procedure:
-summarize the procedure
- PFD is shown
• Discuss the responses form the chart graph.