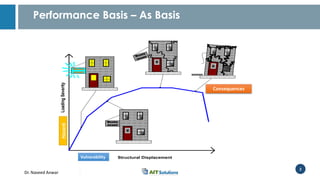
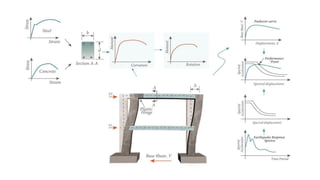
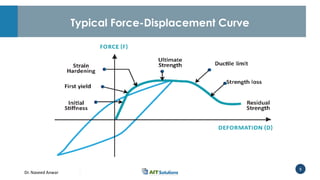
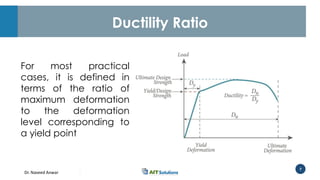
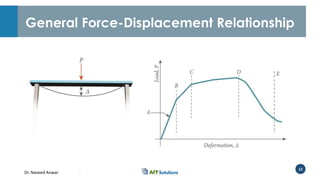
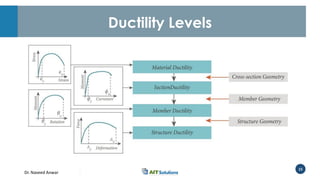
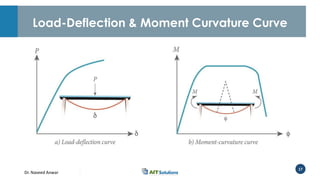
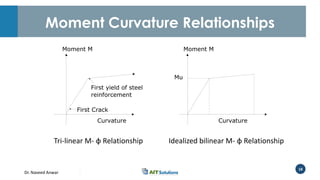
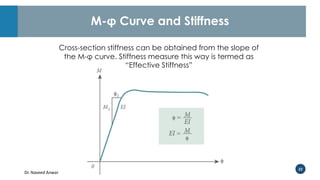
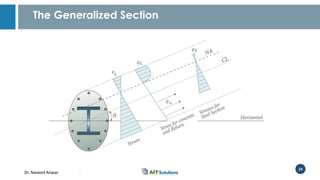
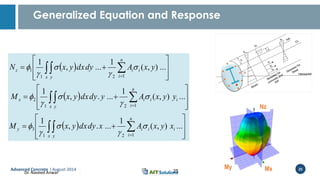
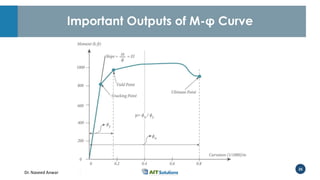
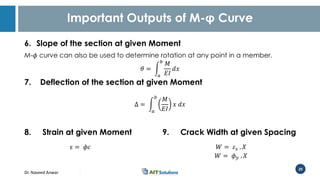
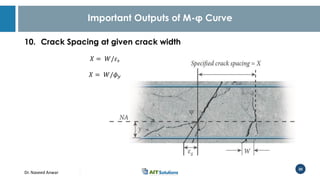
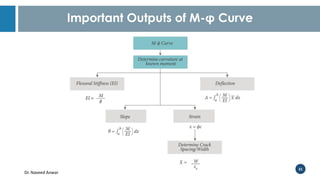
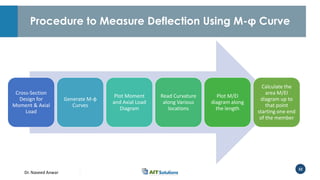
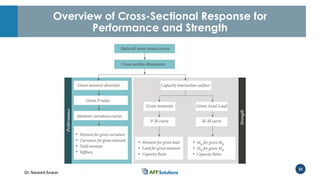
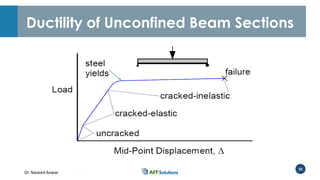
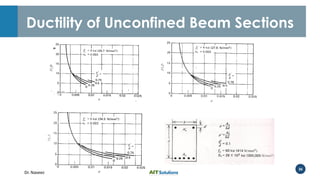
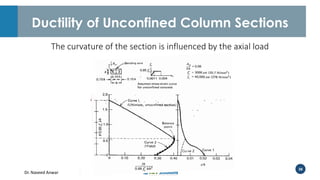
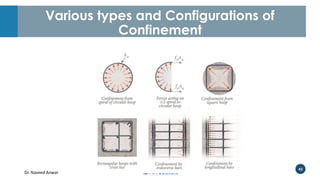
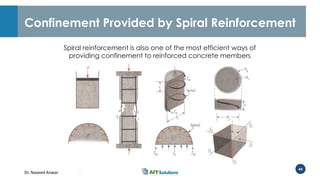
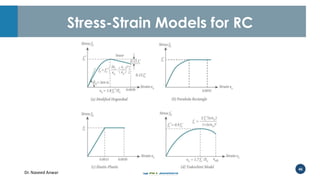
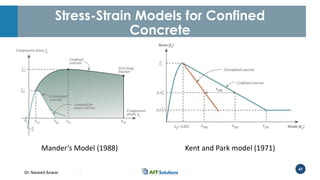
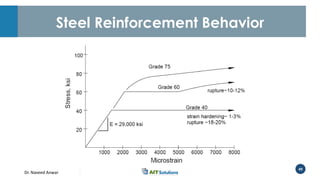
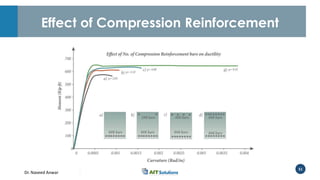
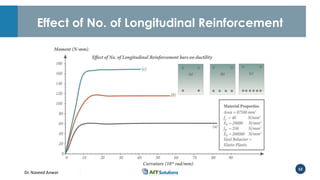
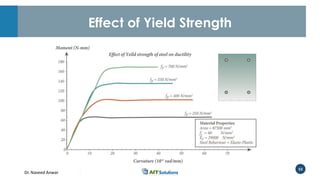
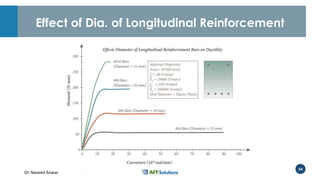
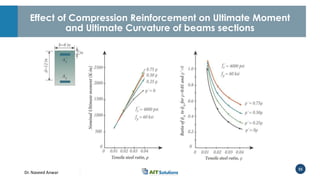
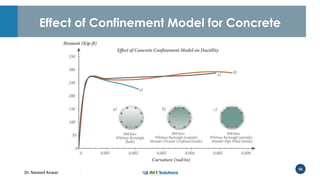
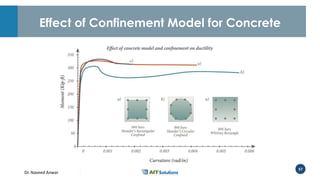
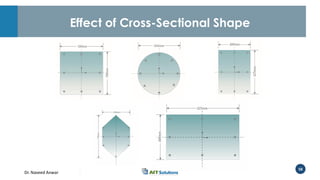
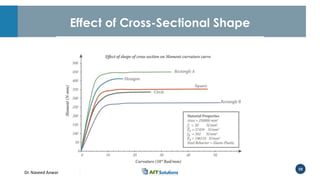
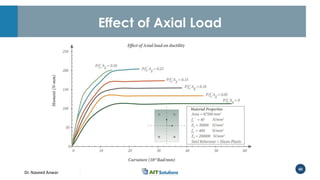
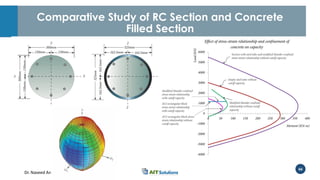
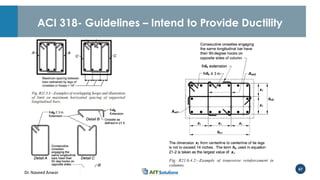
Dr. Naveed Anwar emphasizes the critical role of ductility in the structural performance and seismic design of tall buildings, highlighting its significance in performance-based design. The document discusses the relationship between various force-deformation curves, the importance of moment-curvature relationships, and the effects of confinement on ductility in reinforced concrete structures. It also reviews the limitations of strength-based design and outlines how ductility can be enhanced through appropriate design methodologies and detailing.

1. Dr. Naveed Anwar
Importance of Ductility in
Structural Performance Analysis
Design of Tall Buildings: Trends and Achievements for
Structural Performance
Bangkok-Thailand
November 7-11, 2016
Naveed Anwar, PhD

2. Dr. Naveed Anwar
2
Performance Basis – As Basis
Structural Displacement
LoadingSeverity
Resta
urant
Resta
urant
Resta
urant
Hazard
Vulnerability
Consequences

3. Dr. Naveed Anwar
3

4. Dr. Naveed Anwar
4
Ductility
is the Key to good
(seismic) performance of Structures
Performance Based Design Relies on Ductility

5. Dr. Naveed Anwar
5
Typical Force-Displacement Curve

6. Dr. Naveed Anwar
6
New Book
Structural Cross-sections
Analysis and Design
Naveed Anwar, Fawad Najam

7. Dr. Naveed Anwar
7
Ductility Ratio
For most practical
cases, it is defined in
terms of the ratio of
maximum deformation
to the deformation
level corresponding to
a yield point

8. Dr. Naveed Anwar
8
Ductility Usage
• Strain-based definition of ductility is used at material level, while
rotation- or curvature- based definition also includes the effect of
shape, size and stiffness of cross-section
• All seismic design codes around the world recognize the
importance of ductility as it plays a vital role in structural
performance against earthquakes.
• Well-detailed steel and reinforced concrete (RC) structures, fulfilling
the ductility requirements of codes are expected to undergo large
plastic deformations with little decrease in strength.

9. Dr. Naveed Anwar
9
Limitations of Strength Based Design
• Cross-sections are capable of resisting a certain value of actions
based on assumed failure criterion
• Actions are obtained often from linear elastic analysis, and are
factored to provide certain factor of safety
• Strength design itself provides no information or control on the level
of deformation produced at that factored load level
• No information about behavior of the member if loads or actions
were to exceed the factored design load

10. Dr. Naveed Anwar
Action Deformation Curves

11. Dr. Naveed Anwar
11
Action-Deformation Curves
• Relationship between action and corresponding deformation
• These relationships can be obtained at several levels
1. The Structural Level: Load - Deflection
2. The Member Level: Moment - Rotation
3. The Cross-section Level: Moment - Curvature
4. The Material Level : Stress-Strain
• The Action-Deformation curves show the entire response of the
structure, member, cross-section or material

12. Dr. Naveed Anwar
12
General Force-Displacement Relationship

13. Dr. Naveed Anwar
13
General Force-Displacement Relationship
Point ‘A’ corresponds to the serviceability design considerations and working
strength or allowable strength design concepts.
Point ‘B’ is the point up to which the relationship between load and deformation
can be considered nearly linear and the deformations are relatively small.
Point ‘C’ roughly corresponds to the ultimate strength considerations or the design
capacity consideration.
Point ‘D’ is the point at which the load value starts to drop with increasing
deformations
Point ‘E’ is the point at which the load value is reduced to just a fraction of ultimate
load (residual strength)

14. Dr. Naveed Anwar
14
How to Get Action-Deformation Curves
1. By actual measurements
• Apply load, measure deflection
• Apply load, measure stress and strain
2. By computations
• Use material models, cross-section dimensions to get Moment-Curvature
Curves
3. By combination of measurement and computations
• Calibrate computation models with actual measurements
• Some parameters obtained by measurement and some by computations

15. Dr. Naveed Anwar
15
Ductility Levels

16. Dr. Naveed Anwar
16
Moment Curvature Relationship
is the Key for computing
Cross-section and Member Ductility

17. Dr. Naveed Anwar
17
Load-Deflection & Moment Curvature Curve

18. Dr. Naveed Anwar
18
Moment Curvature Relationships
First Crack
First yield of steel
reinforcement
Moment M
Curvature
Moment M
Curvature
Mu
Tri-linear M- φ Relationship Idealized bilinear M- φ Relationship

19. Dr. Naveed Anwar
19
Moment Curvature (M-φ) Curve
• The load-deformation curves can be plotted between axial load and axial
shortening, shear force and shear deformation, moment and curvature, and
torsion and twist.
• Moment-curvature relationship is probably the most important and useful action-
deformation curve especially for flexural members such as beams, columns and
shear walls.
• Many of the design codes and design procedures or design handbooks do not
provide sufficient information for computation and use of M- relationships

20. Dr. Naveed Anwar
20
Determination of M-φ Curve
• The generation of moment curvature curve can be terminated
based on any number of specific conditions such as,
 The maximum specified strain is reached.
 The first rebar reaches yield stress a any other strain level
 The concrete reaches a certain strain level.
 Also, during the generation of the moment curvature curve the failure
or key response points can be recorded and displayed on the curve.

21. Dr. Naveed Anwar
21
Significance of Moment Curvature Curve
• Information provided by M-φ curve is very useful for non-linear
analysis of structures including the evaluation of post-elastic
behavior.
• M-φ Curve is basis for the capacity-based, and performance-
based design methods especially analysis of structures using
nonlinear static procedures as well as in determining the rotational
capacity of plastic hinges formed during high seismic activity.

22. Dr. Naveed Anwar
22
M-φ Curve and Stiffness
Cross-section stiffness can be obtained from the slope of
the M-φ curve. Stiffness measure this way is termed as
“Effective Stiffness”

23. Dr. Naveed Anwar
23
Unified Cross-section
Models

24. Dr. Naveed Anwar
24
The Generalized Section

25. Dr. Naveed Anwar
25
Generalized Equation and Response
25
 
 
 





























 



...),(
1
....,
1
...),(
1
....,
1
...),(
1
...,
1
121
3
121
2
121
1
i
n
i
ii
x y
y
i
n
i
ii
x y
x
x y
n
i
iiz
xyxAxdydxyxM
yyxAydydxyxM
yxAdydxyxN















Nz
MxMyAdvanced Concrete l August-2014
y
h
c
fc
Strain
Stresses for
concrete and
R/F
Stresses for
Steel
f1
f2
fn
fs NA
CL
Horizontal

26. Dr. Naveed Anwar
26
Important Outputs of M-φ Curve

27. Dr. Naveed Anwar
27
Important Outputs of M-φ Curve
1. Cracking Point
This point corresponds to the onset of material cracking of a cross-section. It
provides the moment and corresponding curvature for design considerations
related to start of cracking
2. Yield Point
This point corresponds to the onset of material yielding of a cross-section. It provides
the moment capacity and corresponding curvature for strength design of section.
3. Failure Point
This point corresponds to the maximum curvature and defines the maximum
deformation capacity of section.

28. Dr. Naveed Anwar
28
Important Outputs of M-φ Curve
4. Ductility
The ratio of ultimate curvature and yield curvature defines the section ductility.
𝜇 = 𝜙 𝑢/𝜙 𝑦
5. Stiffness of the Section at given M and 𝝓
Slope of M-𝜙 curve at any given point corresponds to the effective stiffness of the
section.
𝜙 =
𝑀
𝐸𝐼
and 𝐸𝐼 =
𝑀
𝜙

29. Dr. Naveed Anwar
29
Important Outputs of M-φ Curve
6. Slope of the section at given Moment
M-𝜙 curve can also be used to determine rotation at any point in a member.
𝜃 =
𝑎
𝑏
𝑀
𝐸𝐼
𝑑𝑥
7. Deflection of the section at given Moment
Δ =
𝑎
𝑏
𝑀
𝐸𝐼
𝑥 𝑑𝑥
8. Strain at given Moment
ε = 𝜙𝑐
9. Crack Width at given Spacing
𝑊 = 𝜀 𝑠 . 𝑋
𝑊 = 𝜙 𝑦 . 𝑋

30. Dr. Naveed Anwar
30
Important Outputs of M-φ Curve
10. Crack Spacing at given crack width
𝑋 = 𝑊/𝜀 𝑠
𝑋 = 𝑊/𝜙 𝑦

31. Dr. Naveed Anwar
31
Important Outputs of M-φ Curve

32. Dr. Naveed Anwar
32
Procedure to Measure Deflection Using M-φ Curve
Cross-Section
Design for
Moment & Axial
Load
Generate M-φ
Curves
Plot Moment
and Axial Load
Diagram
Read Curvature
along Various
locations
Plot M/EI
diagram along
the length
Calculate the
area M/EI
diagram up to
that point
starting one end
of the member

33. Dr. Naveed Anwar
33
Overview of Cross-Sectional Response for
Performance and Strength

34. Dr. Naveed Anwar
Ductility of Unconfined Beam &
Column Sections

35. Dr. Naveed Anwar
35
Ductility of Unconfined Beam Sections

36. Dr. Naveed Anwar
36
Ductility of Unconfined Beam Sections

37. Dr. Naveed Anwar
37
Ductility of Unconfined Column Sections
• The curvature of the section is influenced by the axial load, hence there
is no unique M-φ relationship for a given column section.
• However, it is possible to plot the combination of axial load P and
Moment M which cause the section to reach the ultimate capacity.
• It is evident that the ductility of the column section is significantly
reduced by the presence of axial load.
• The axial load levels greater than the balanced failure load, the ductility
decreases, being due only to the inelastic deformation of the concrete.

38. Dr. Naveed Anwar
38
Ductility of Unconfined Column Sections
The curvature of the section is influenced by the axial load

39. Dr. Naveed Anwar
Ductility of Confinement of RC
Sections

40. Dr. Naveed Anwar
40
Confinement
is the Key for Ductility in Reinforced
Concrete Members

41. Dr. Naveed Anwar
41
Confinement of RC Sections
Poisson’s effect for compressive force
Concrete sample wrapped with a suitably strong material
(e.g. carbon fiber), becomes impossible to crush

42. Dr. Naveed Anwar
42
Confinement of RC Sections
• Ductility can be improved if confining is done in such a way that the
concrete sample is allowed to expand very slowly.
• In RC members, concrete is confined using rectangular or circular steel
reinforcement hoops.
• One RC cross section have 2 types of concrete, i.e. the confined
concrete in the inner core and the cover concrete outside the core.
• Double confinement using multiple hoops is also quite common is bridges.
For RC columns, more attention is given to vertical reinforcement than
lateral reinforcement. However, most of the axial strength is contributed
by the lateral reinforcement

43. Dr. Naveed Anwar
43
Various types and Configurations of
Confinement

44. Dr. Naveed Anwar
44
Confinement Provided by Spiral Reinforcement
Spiral reinforcement is also one of the most efficient ways of
providing confinement to reinforced concrete members

45. Dr. Naveed Anwar
45
Confinement Provided by Spiral Reinforcement
Comparison of axial force-deformation behaviors of reinforced concrete columns
with various confinement configurations

46. Dr. Naveed Anwar
46
Stress-Strain Models for RC

47. Dr. Naveed Anwar
47
Stress-Strain Models for Confined
Concrete
Mander’s Model (1988) Kent and Park model (1971)

48. Dr. Naveed Anwar
48
Stress-Strain Models for Confined Concrete
Mander’s
stress-strain
Model
(1988)
Kent and
Park stress-
strain model
(1971)
Scott et al.
stress-strain
model
(1982)
Yong et al.
stress-strain
model
(1989)
Bjerkeli et al.
stress-strain
model
(1990)
Li et al.
stress-strain
model
(2000)

49. Dr. Naveed Anwar
49
Steel Reinforcement Behavior

50. Dr. Naveed Anwar
Factors Affecting Moment-Curvature
Relationship and Ductility of RC Sections

51. Dr. Naveed Anwar
51
Effect of Compression Reinforcement

52. Dr. Naveed Anwar
52
Effect of No. of Longitudinal Reinforcement

53. Dr. Naveed Anwar
53
Effect of Yield Strength

54. Dr. Naveed Anwar
54
Effect of Dia. of Longitudinal Reinforcement

55. Dr. Naveed Anwar
55
Effect of Compression Reinforcement on Ultimate Moment
and Ultimate Curvature of beams sections

56. Dr. Naveed Anwar
56
Effect of Confinement Model for Concrete

57. Dr. Naveed Anwar
57
Effect of Confinement Model for Concrete

58. Dr. Naveed Anwar
58
Effect of Cross-Sectional Shape

59. Dr. Naveed Anwar
59
Effect of Cross-Sectional Shape

60. Dr. Naveed Anwar
60
Effect of Axial Load

61. Dr. Naveed Anwar
Concrete Filled Tubes

62. Dr. Naveed Anwar
62
Lateral Stresses in Concrete Filled Tubes
Circular steel tubing will have the greatest confining effect as
compared to other shapes

63. Dr. Naveed Anwar
63
Advantages of Concrete Filled Tubes
Avoid
inward
buckling of
steel
High
strength and
ductility
Ease of
Construction
Avoids
Premature
Spalling of
Concrete

64. Dr. Naveed Anwar
64
Various forms of Concrete Filled Tubes

65. Dr. Naveed Anwar
65
Efficient Bonding between Steel Tube and
Concrete Cores
Efficient
Bonding
Use of
Mechanical
Connectors
Interlock at
Concrete
and Steel
Interface
Friction
between
Materials
Adhesion
due to
Chemical
Actions
Creep in
Concrete

66. Dr. Naveed Anwar
66
Comparative Study of RC Section and Concrete
Filled Section

67. Dr. Naveed Anwar
67
ACI 318- Guidelines – Intend to Provide Ductility

68. Dr. Naveed Anwar
68
It is important to recognize, explicitly
evaluate and provide Ductility in key
locations and members for improved
performance for extreme loads

69. Dr. Naveed Anwar
69
View publication statsView publication stats