Uploaded byDenpong Soodphakdee
7,529 views
Engineering Equation Solver (Thai)
This document introduces the Engineering Equation Solver (EES) software. EES is a general purpose equation solver and modeling tool designed for engineering education. It allows users to solve systems of nonlinear equations without programming by using an implicit iterative solver. EES includes features such as built-in properties, functions, units support, and parametric studies. Tutorial examples are provided to demonstrate solving equations, formatting equations, and performing a parametric study to analyze the maximum distance traveled by a projectile.
More Related Content
What's hot
Viewers also liked
Similar to Engineering Equation Solver (Thai)
More from Denpong Soodphakdee
In this document
Powered by AI
Introduction to Engineering Equation Solver (EES) for education, its advantages, and features.
Methodology for solving nonlinear equations using EES, including practical tutorials on inputting equations.
Details on formatting equations and variables, types of comments, and the handling of constants.
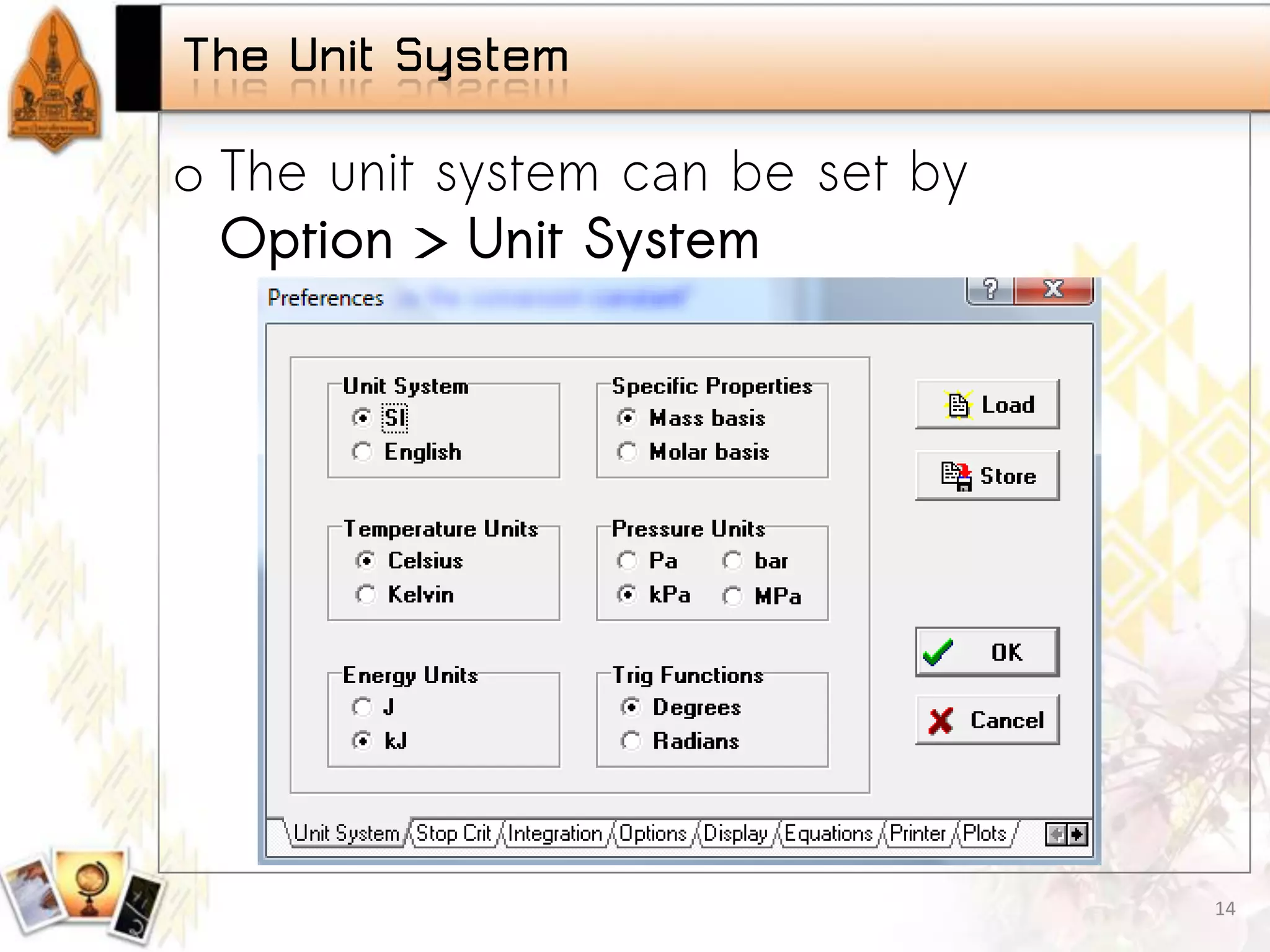
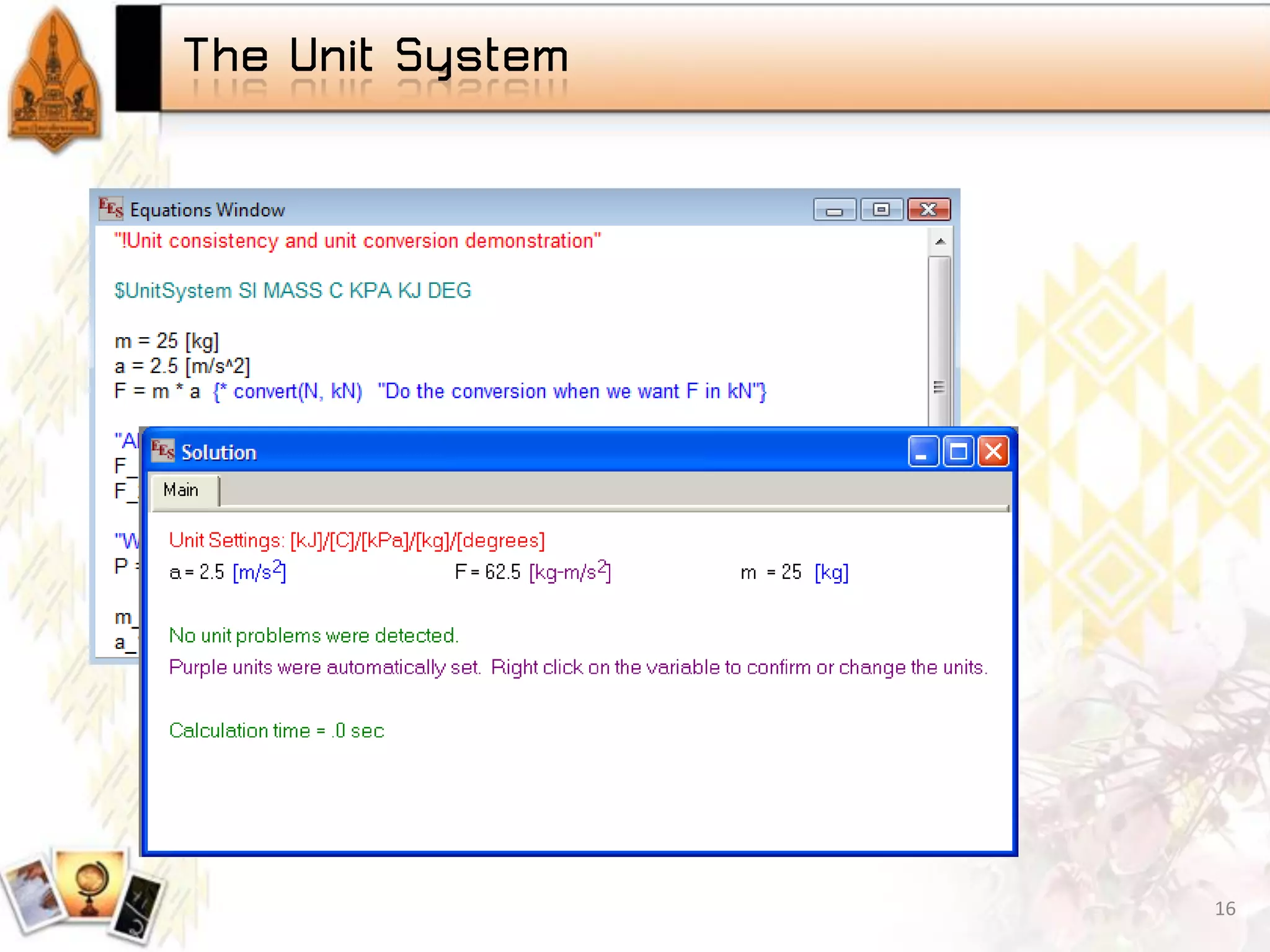
Unit system setup, unit conversions, and examples of assigning units in EES.
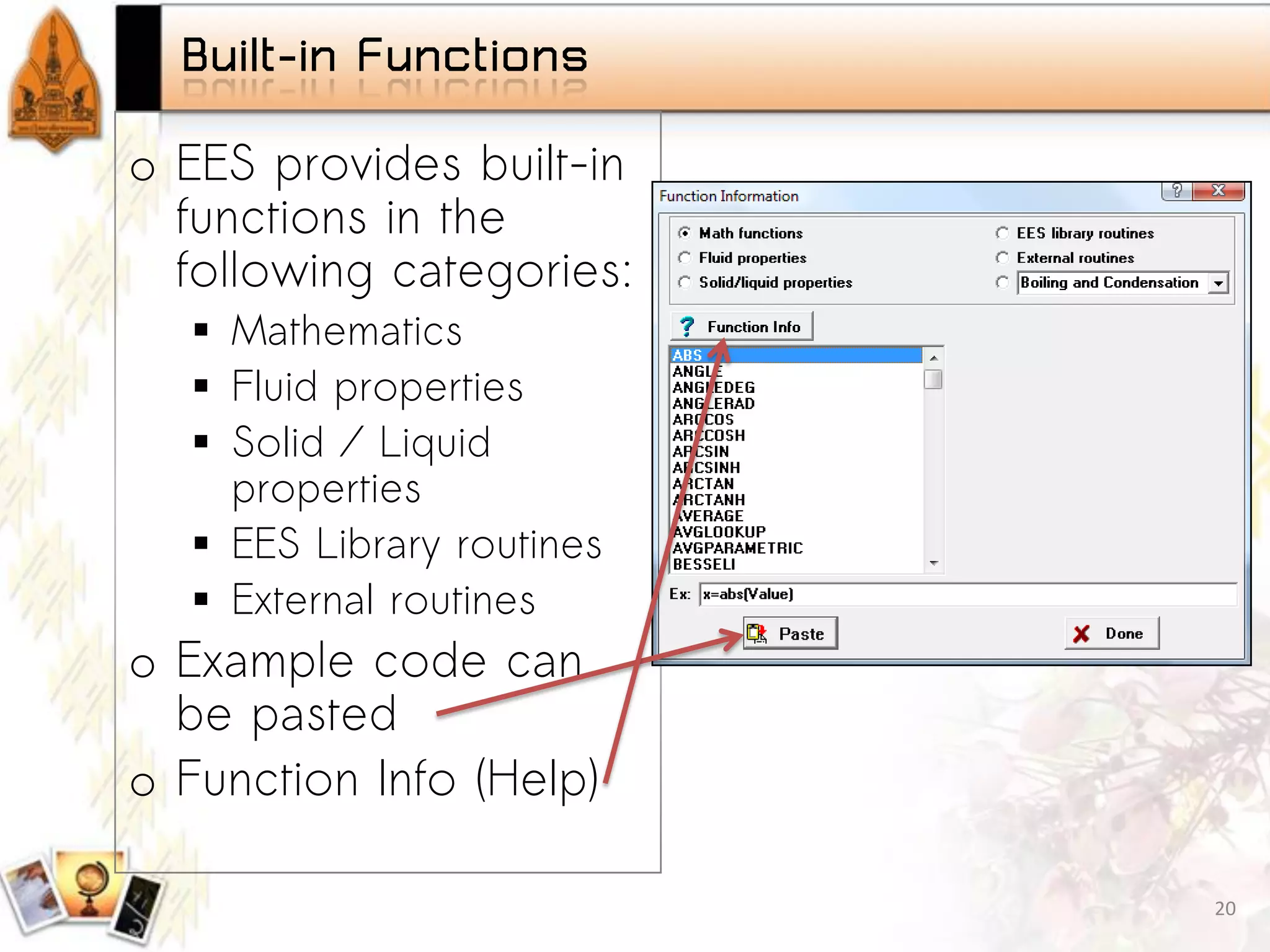
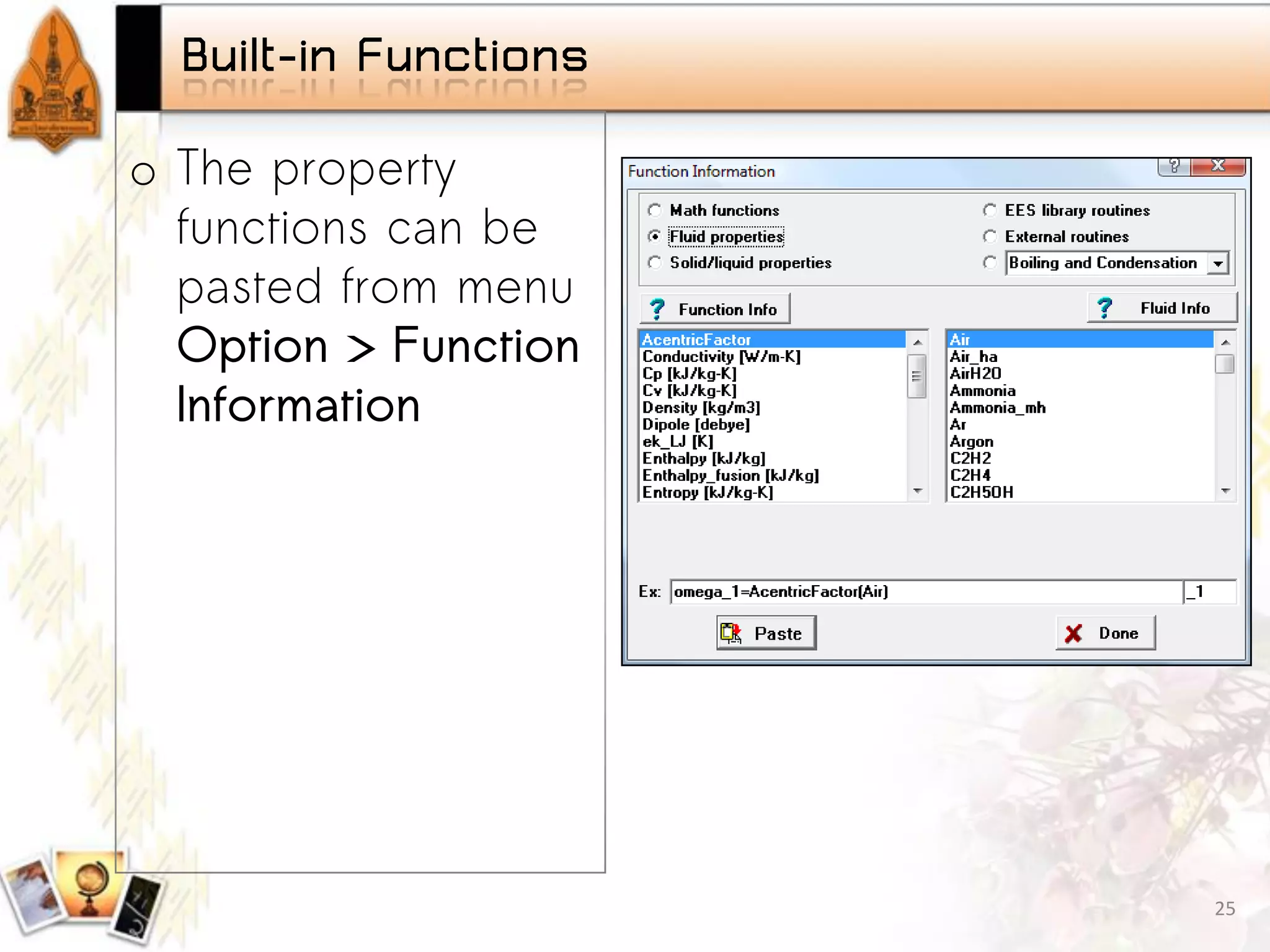
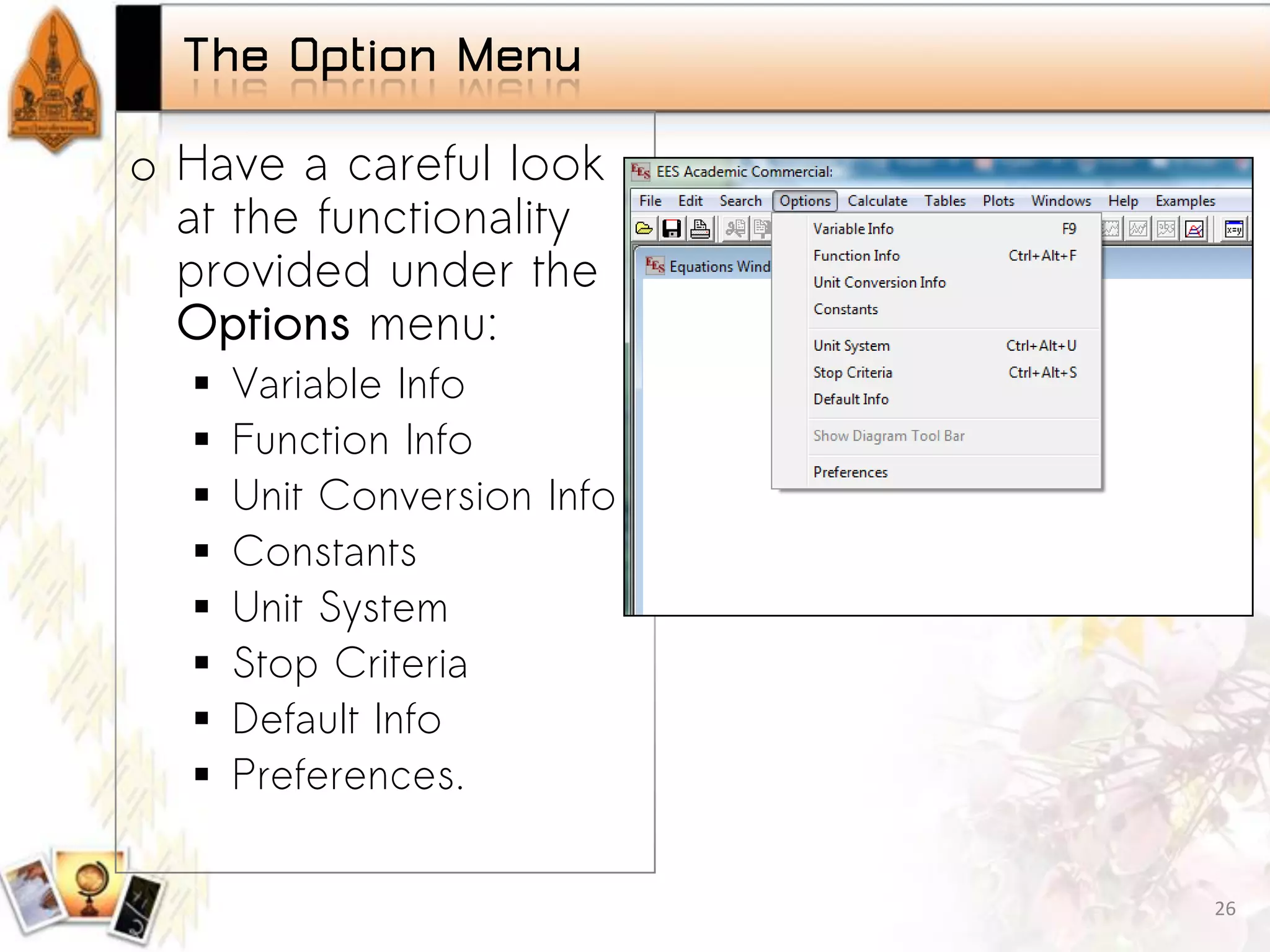
Overview of built-in functions, including mathematical operations and property functions.
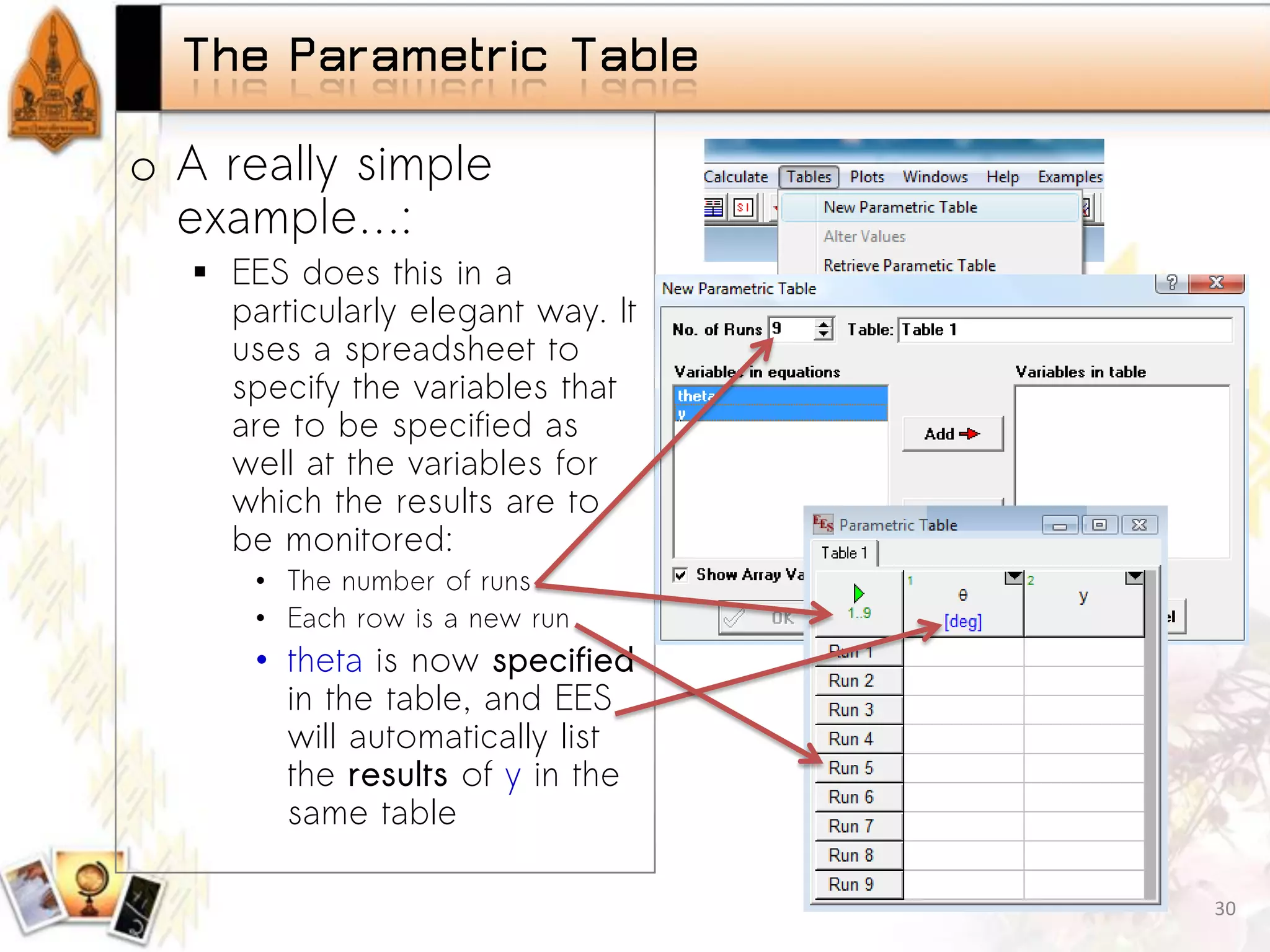
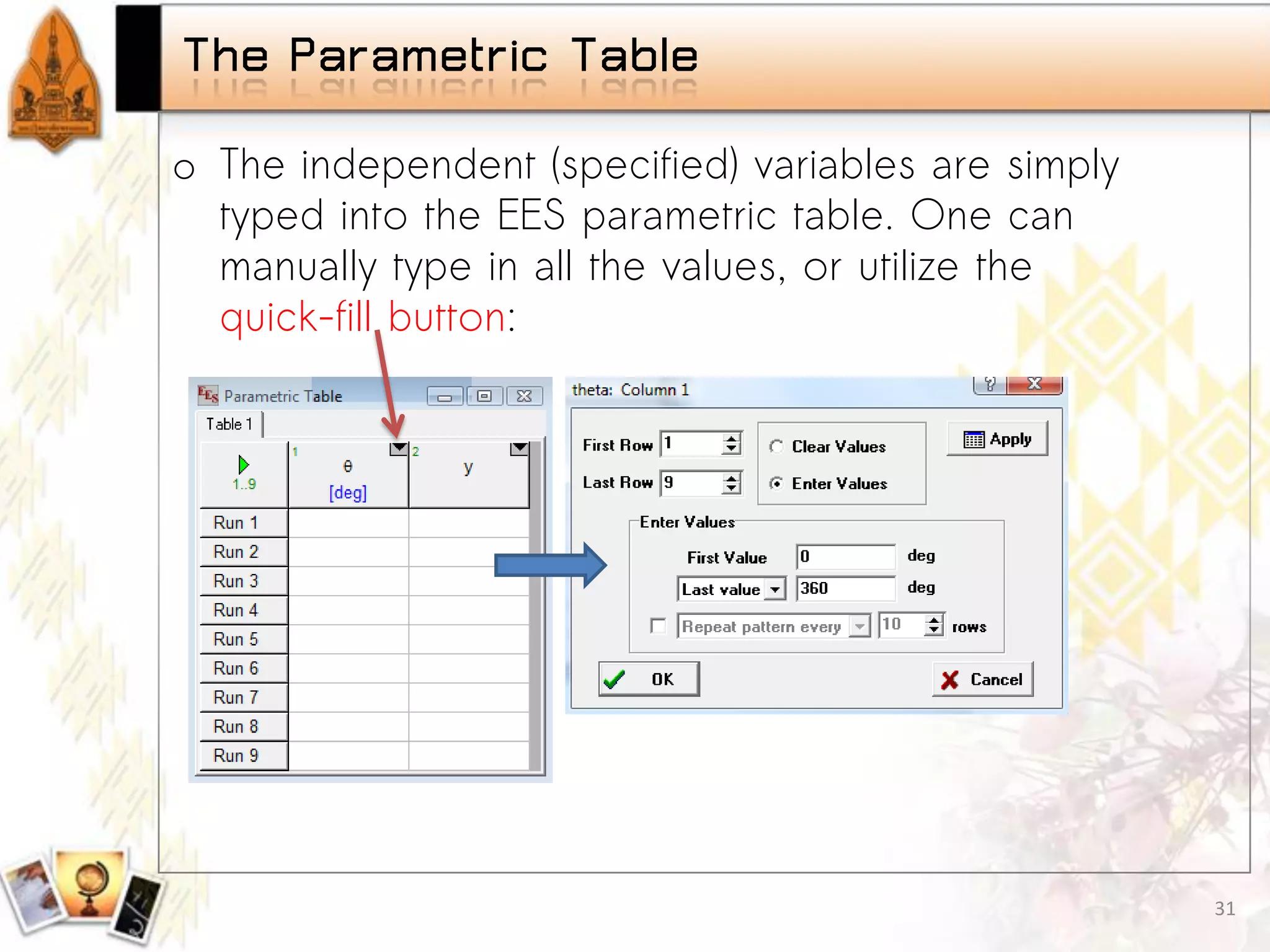
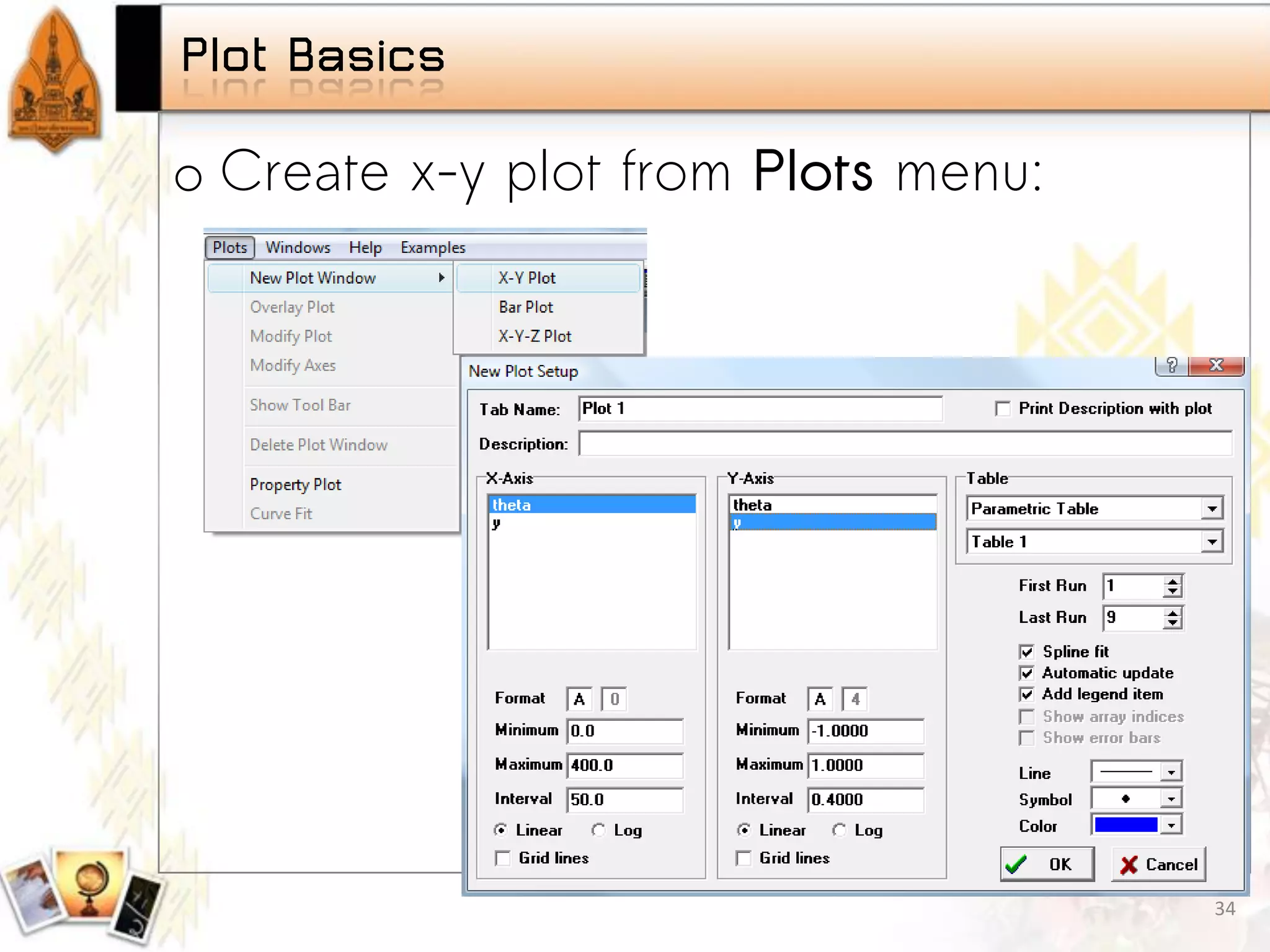
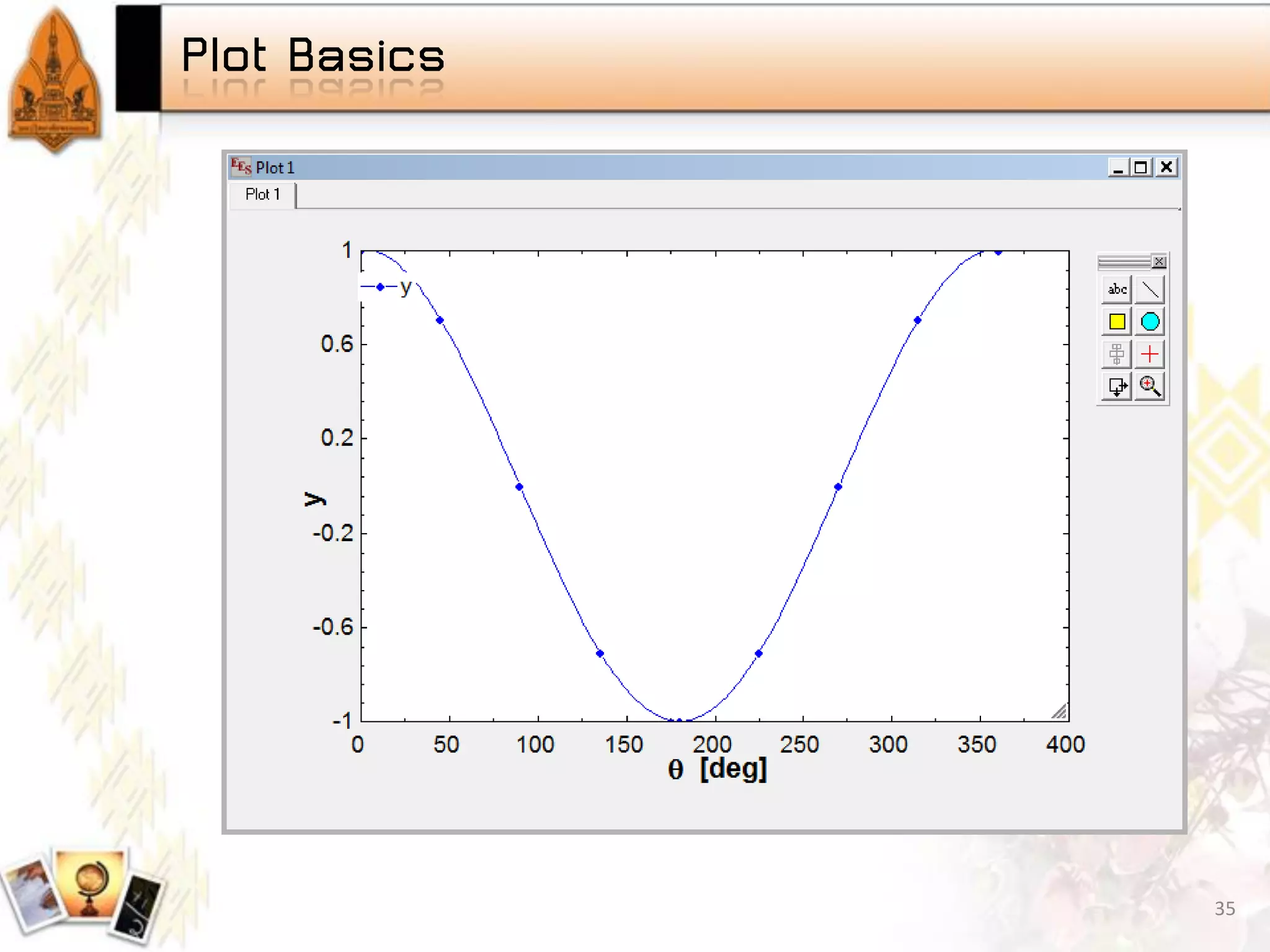
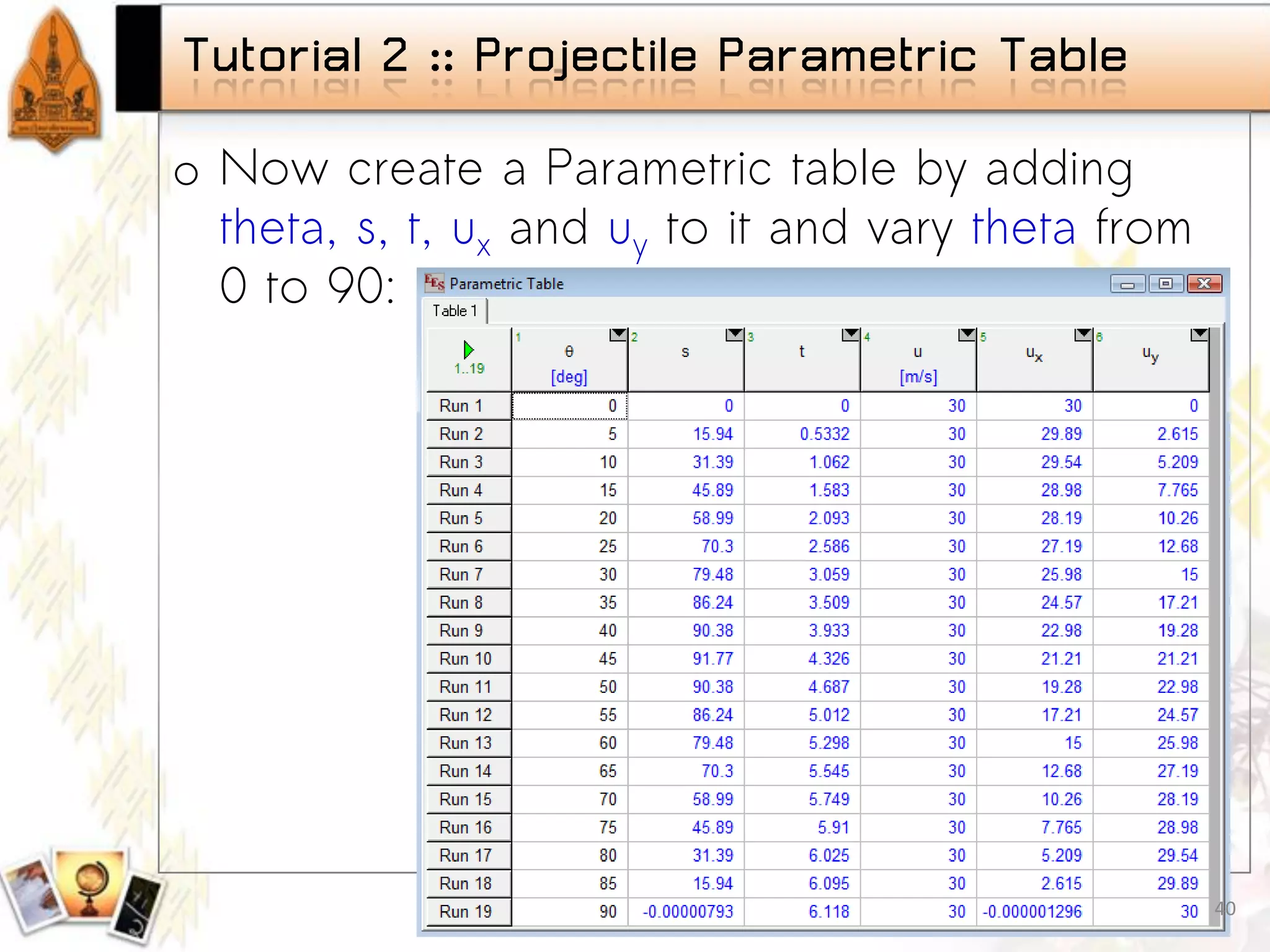
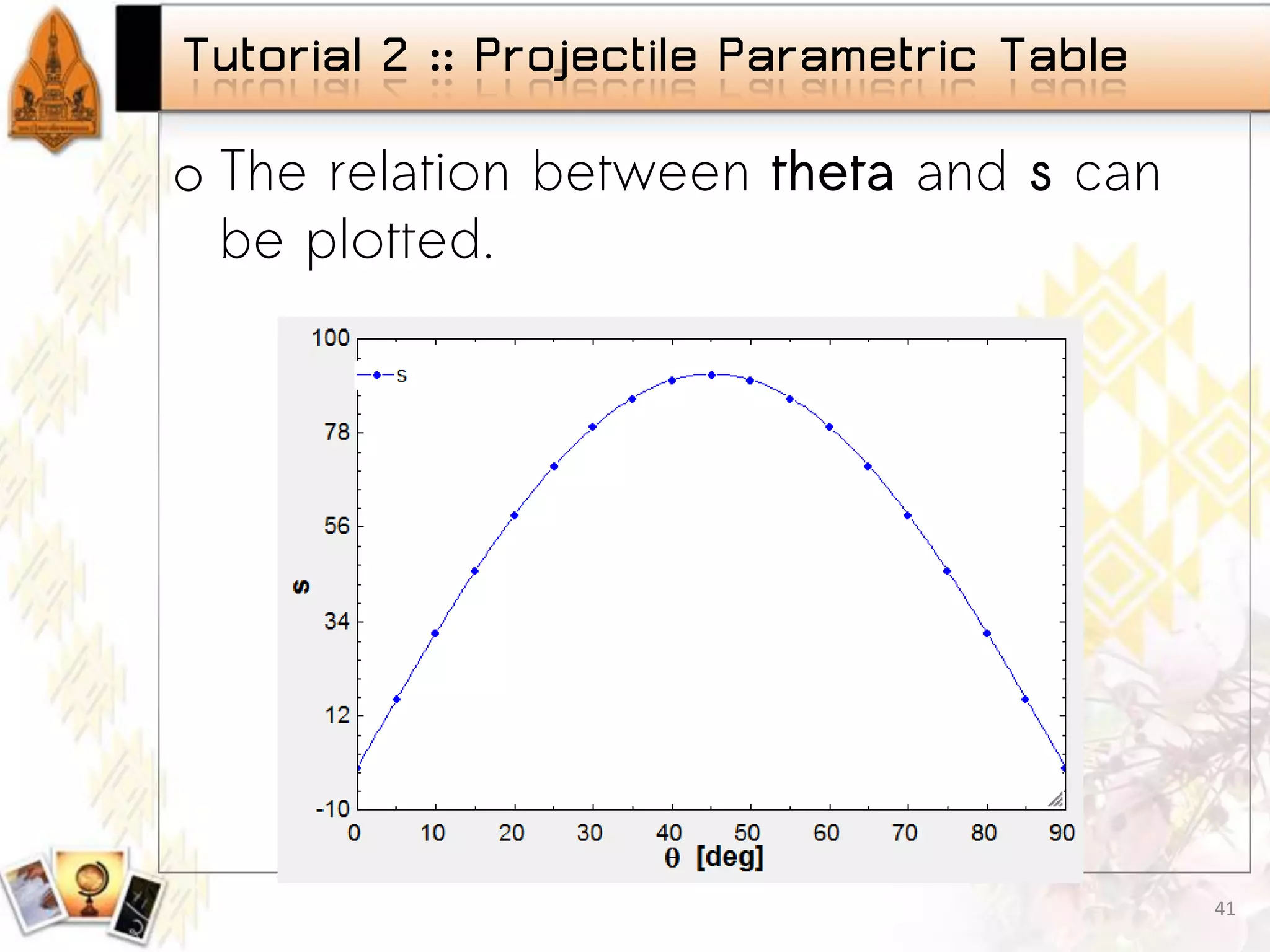
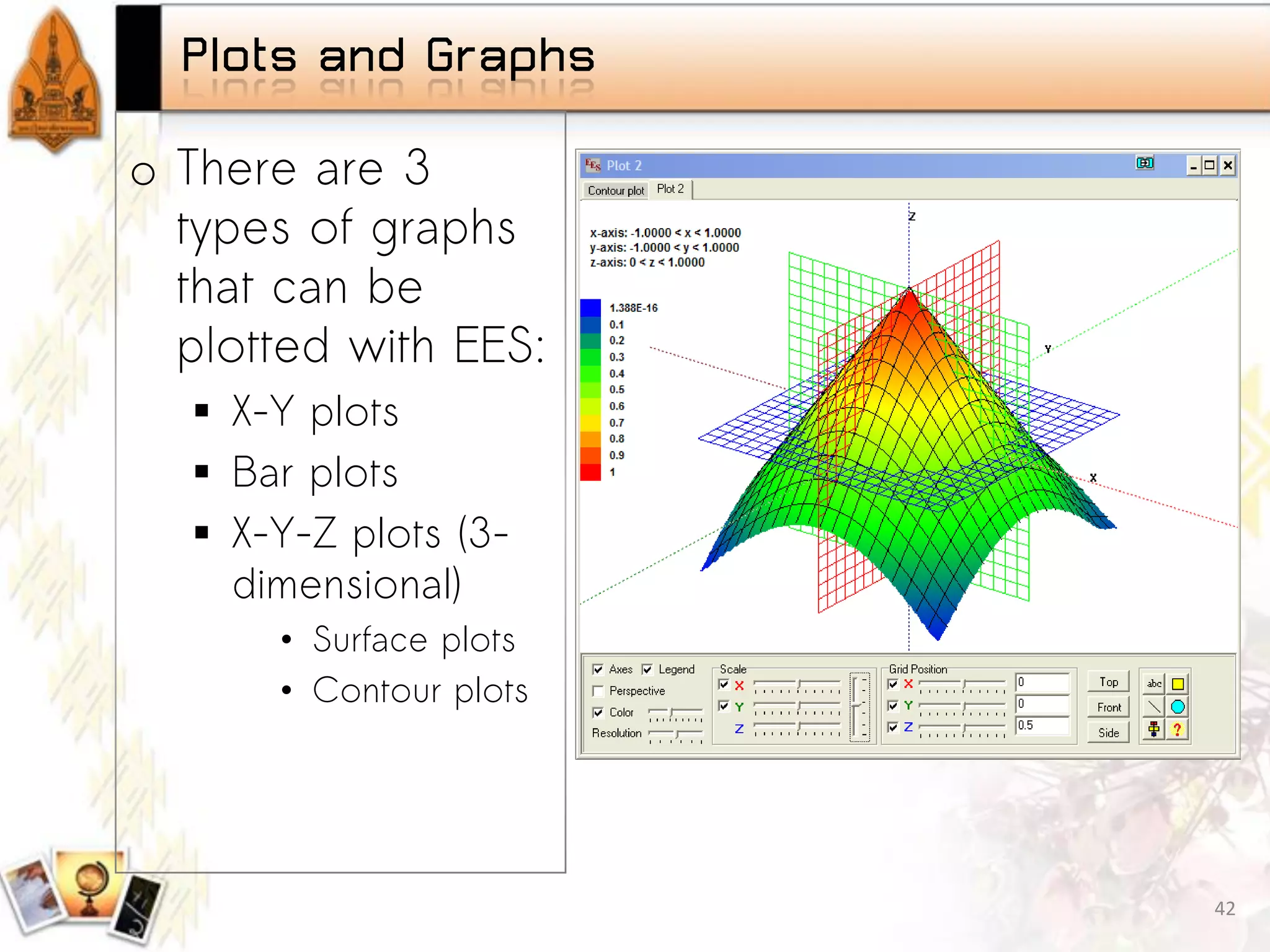
Introduction to parametric studies in EES, examples showcasing the implementation and findings. Fundamentals of plotting data in EES, types of graphs available, and tutorial on projectile motion.