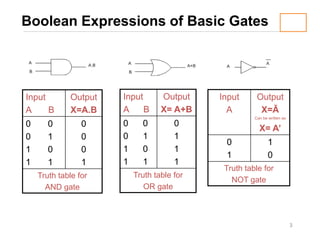
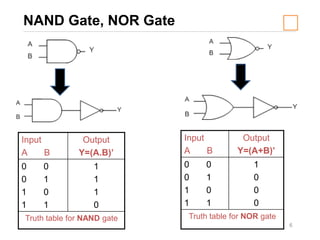
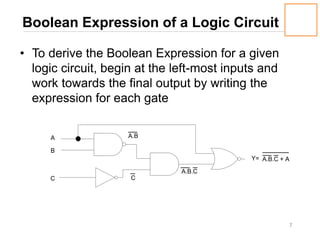
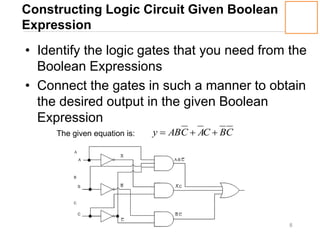
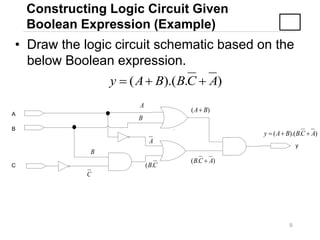
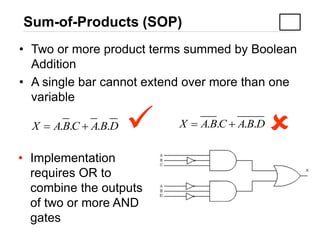
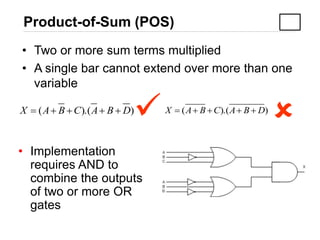
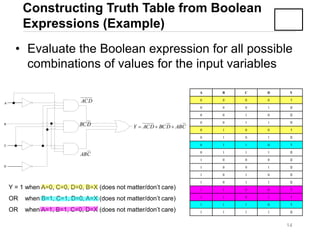
This document discusses Boolean algebra concepts including logic gates, Boolean expressions, truth tables, and logic circuit design. It covers: 1) The definitions and truth tables of common logic gates like AND, OR, NAND, and NOR. 2) How to derive the Boolean expression of a logic circuit and construct a circuit from a given Boolean expression. 3) Converting between Sum of Products (SOP) and Product of Sums (POS) forms using techniques like standard SOP from a truth table.

1. 1
Further logic concepts
• NAND, NOR, XOR gates, utility of universal
logic functions,Boolean expressions of NAND
and NOR gate
• How to derive output Boolean expression of
given logic circuit.
• How to construct truth table given Boolean
expression
• How to draw logic circuit schematic given
Boolean expression.
• Obtain output Boolean Expressions in SOP and
POS form

2. 2
Variable, Literal (in Boolean Expressions)
• Variable is a symbol used to represent a logical
quantity
• Any variable can have a 1 or 0 value
• The complement of a variable A is indicated by
Ā or A’ (read as A bar)
• Literal is a variable or the complement of a
variable

3. 3
Boolean Expressions of Basic Gates
Input
A B
Output
X= A+B
0 0
0 1
1 0
1 1
0
1
1
1
Truth table for
OR gate
Input
A B
Output
X=A.B
0 0
0 1
1 0
1 1
0
0
0
1
Truth table for
AND gate
Input
A
Output
X=Ā
Can be written as
X= A’
0
1
1
0
Truth table for
NOT gate

4. 4
Boolean Addition
• Boolean Addition is equivalent to the OR
operation
• Basic rules for Boolean Addition:
1 + 1 = 1
1 + 0 = 1
0 + 1 = 1
0 + 0 = 0
• A sum term is equal to 1 when one or more
literals in the term are 1
• A sum term is equal to 0 only if each of the
literals is 0

5. 5
Boolean Multiplication
• Boolean Multiplication is equivalent to the AND
operation
• Basic rules for Boolean Addition:
1.1 = 1
1.0 = 0
0.1 = 0
0.0 = 0
• A product term is equal to 1 only if each of the
literals in the term is 1
• A product term is equal to 0 when one or more
literals are 0

6. 6
NAND Gate, NOR Gate
Input
A B
Output
Y=(A.B)’
0 0
0 1
1 0
1 1
1
1
1
0
Truth table for NAND gate
Input
A B
Output
Y=(A+B)’
0 0
0 1
1 0
1 1
1
0
0
0
Truth table for NOR gate

7. 7
Boolean Expression of a Logic Circuit
• To derive the Boolean Expression for a given
logic circuit, begin at the left-most inputs and
work towards the final output by writing the
expression for each gate
A
B
C
Y=
A.B
C
A.B.C
A.B.C + A

8. 8
Constructing Logic Circuit Given Boolean
Expression
• Identify the logic gates that you need from the
Boolean Expressions
• Connect the gates in such a manner to obtain
the desired output in the given Boolean
Expression
CBCACABy ++=The given equation is:

9. 9
Constructing Logic Circuit Given
Boolean Expression (Example)
• Draw the logic circuit schematic based on the
below Boolean expression.
).).(( ACBBAy ++=
`
A
B
C
y
).).(( ACBBAy ++=
)( BA+
).( ACB +
A
B
A
CB.(
B
C

10. Sum-of-Products (SOP)
• Two or more product terms summed by Boolean
Addition
• A single bar cannot extend over more than one
variable
DBACBAX .... +=DBACBAX .... += ✓ 
• Implementation
requires OR to
combine the outputs
of two or more AND
gates

11. Product-of-Sum (POS)
• Two or more sum terms multiplied
• A single bar cannot extend over more than one
variable
✓ 
• Implementation
requires AND to
combine the outputs
of two or more OR
gates
)).(( DBACBAX ++++=)).(( DBACBAX ++++=

12. Standard SOP from Truth Table
• List the binary values of the input variables for
which the output is 1
• Convert each binary value to the corresponding
product term by:
✓ Replacing 1 with corresponding variable
✓ Replacing 0 with corresponding variable complement
• These product terms which are composed of
every input variable or its complement ANDed
together are known as minterms
• Sum these minterms together

13. Standard POS from Truth Table
• List the binary values of the input variables for
which the output is 0
• Convert each binary value to the
corresponding sum term by:
✓ Replacing 0 with corresponding variable
✓ Replacing 1 with corresponding variable
complement
• These sum terms which are composed of
every input variable or its complement ORed
together are known as maxterms
• Multiply these maxterms together

14. 14
Constructing Truth Table from Boolean
Expressions (Example)
• Evaluate the Boolean expression for all possible
combinations of values for the input variables
Y = 1 when A=0, C=0, D=0, B=X (does not matter/don’t care)
OR when B=1, C=1, D=0, A=X (does not matter/don’t care)
OR when A=1, B=1, C=0, D=X (does not matter/don’t care)
A B C D Y
0 0 0 0 1
0 0 0 1 0
0 0 1 0 0
0 0 1 1 0
0 1 0 0 1
0 1 0 1 0
0 1 1 0 1
0 1 1 1 0
1 0 0 0 0
1 0 0 1 0
1 0 1 0 0
1 0 1 1 0
1 1 0 0 1
1 1 0 1 1
1 1 1 0 1
1 1 1 1 0
A
B
C
D
Y
DCA
DBC
CAB
CABDBCDCAY ++=