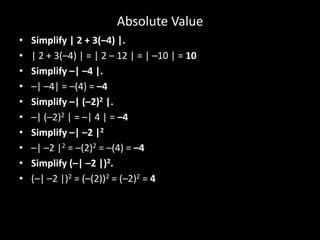The document discusses absolute value, noting that absolute value represents the distance from zero regardless of direction. It provides examples of simplifying expressions involving absolute value, and explains that the absolute value of a variable depends on whether the variable is positive or negative.

1. September 20, 2012

2. 1. Khan Academy Registration: There are a few people whose name I
cannot tell from their login name. Please check your email. You are
not getting credit as of now if I don't know who you are.
2. New Khan Mastery Topics posted for the rest of September and all
of October. This should take us to the end of the 1st quarter.
3. Bonus Points: Every few days, a bonus question is posted on the
v6math site. First 5 people who email the correct answer get 10 xtra
credit pts. Those 5 get email. If no email, then you were too late.
4. The library is open from 7:00 a.m. - 4:00 p.m. if you do not have
internet access for the Khan Academy.
5. The last quiz was not graded: 2nd/4th
6. Text/Work Book for download: Pls. do this.

3. September 20, 2012
Review: Integers, Expressions, Translations, Order of
Operations, Distributive Property
Class work: Order of Operations, Distributive Prop.
1. There are two ways to combine long strings of integers.
A. Add all the positive numbers, then add all the negative
numbers. Then combine the two numbers using rule for
opposite signs.
B. Combine all numbers in order from left to right.
Use method A for these numbers:
-3 + (-5) + 6 + 9 + 2 + (-4)
6 + 9 + 2 = 17; -3 + (-5) + (-4) = -12; 17 - 12 = 5
Use Method B: 5 + (-4) + (-6) + 8 + (-3) + 3 =
1 -6 = -5 + 8 = 13 - 3 = -0 + 3 = 13

4. Integer Practice
1. -3+(-5) = 2. 3.2 + (-5.2) = 3. -7 + (-5) =
4. 24 + (-11) = 5. 50 + (-8) = 6. -31 + 25 =
1. -8 2. -2 3. -12 4. 13 5. 42 6. -6
7. -31 + 19 + (-25) 8. -6 + (-2) + (-3) 9. -2 - (-19)
7. -37 8. -11 9. 17
10. (-3)(-5)(-3) 11. -4ab • (-6) 12. (-4)(-2)(8r)
13. -28 ÷ (-4) 14. 35/-7 15. -25/-5
10. -45 11. 24ab 12. 64r 13. 7 14. -5 15. 5

5. Simplifying Expressions
1. 4 + m - 3m 2. 10 - 4x + 2x -3 3. -8(r + 6) - r + 1
1. 4 - 2m 2. 7 - 2x 3. -9r - 47 or 9r + 47
4. -6x - 5 + 2/3(24x -12) 5. 13x + 5y - 4x
4. 10x + 3 5. 9x + 5y
The Distributive Property
1. -5(w - 8) 2. 0.5(20 + 9) 3. 7(8 + 0.4) 4. 8(3x + 4y)
1. -5w + 40 2. 14.5 3. 56+ 2.4 = 58.4 4. 24x + 32y

6. Order of Operations
1. 5 • 102 = 2. (23 • 32) ÷ 6 = 3. 33 + (9 •3) - 10 =
1. 5 • 100 = 500 2. (72) ÷ 6 = 12 3. 60 - 10 = 50
Lastly, Translation
1. The A's played 72 games. They won 10 more games
than they lost. How many games did they win and lose?
2. A Limousine bill totaled $510. This included a $150 service
charge and 6 hours of use. What was the hourly rate for the
Limo?
Homework: Order of Operations, Distributive
Property: Girls--Even, Guys--Odd

7. September 21, 2012
• Absolute Value: The absolute value of x, denoted "| x |" (and
which is read as "the absolute value of x"), is the distance of x
from zero. This is why absolute value is never negative; absolute
value only asks "how far?", not "in which direction?" This means
not only that | 3 | = 3, because 3 is three units to the right of
zero, but also that | –3 | = 3, because –3 is three units to the
left of zero.
• Warning: The absolute-value notation is bars, not parentheses
or brackets. Use the proper notation; the other notations do not
mean the same thing.

8. Absolute Value
• It is important to note that the absolute value bars do NOT
work in the same way as do parentheses. Whereas –(–3) = +3,
this is NOT how it works for absolute value:
• Simplify –| –3 |.
• Given –| –3 |, I first handle the absolute value part, taking the
positive and converting the absolute value bars to
parentheses:
• –| –3 | = –(+3)
• Now I can take the negative through the parentheses:
• –| –3 | = –(3) = –3
• As this illustrates, if you take the negative of an absolute
value, you will get a negative number for your answer.

9. Absolute Value
• Here are some more sample simplifications:
• Simplify | –8 |. | –8 | = 8
• Simplify | 0 – 6 |. | 0 – 6 | = | –6 | = 6
• Simplify | 5 – 2 |. |5–2|=|3|=3
• Simplify | 2 – 5 |. | 2 – 5 | = | –3 | = 3
• Simplify | 0(–4) |. | 0(–4) | = | 0 | = 0

10. Absolute Value
• Simplify | 2 + 3(–4) |.
• | 2 + 3(–4) | = | 2 – 12 | = | –10 | = 10
• Simplify –| –4 |.
• –| –4| = –(4) = –4
• Simplify –| (–2)2 |.
• –| (–2)2 | = –| 4 | = –4
• Simplify –| –2 |2
• –| –2 |2 = –(2)2 = –(4) = –4
• Simplify (–| –2 |)2.
• (–| –2 |)2 = (–(2))2 = (–2)2 = 4

11. • Sometimes you will be asked to insert an inequality sign
between two absolute values, such as:
• Insert the correct inequality: | –4 | _____ | –7 |
• Whereas –4 > –7 (because it is further to the right on the
number line than is –7), I am dealing here with the absolute
values. Since:
• | –4 | = 4
• | –7 | = 7,
• ...and since 4 < 7, then the solution is:
• | –4 | < | –7 |.

12. • When the number inside the absolute value (the "argument"
of the absolute value) was positive anyway, we didn't change
the sign when we took the absolute value. But when the
argument was negative, we did change the sign; namely, we
changed the "understood" "plus" into a "minus". This leads to
one fiddly point which may not come up in your homework
now, but will probably show up on tests later:
• When you are dealing with variables, you cannot tell the sign
of the number or the value that is contained in the variable.
For instance, given the variable x, you cannot tell by looking
whether there is, say, a "2" or a "–4" contained inside. If I ask
you for the absolute value of x, what would you do? Since you
cannot tell, just by looking at the letter, whether or not the
variable contains a positive or negative value, you would have
to consider these two different cases.

13. • If x > 0 (that is, if x is positive), then the value won't change
when you take the absolute value. For instance, if x = 2, then
you have | x | = | 2 | = 2 = x. In fact, for any positive value of x
(or if x equals zero), the sign would be unchanged, so:
• For x > 0, | x | = x
• On the other hand, if x < 0 (that is, if x is negative), then it will
change its sign when you take the absolute value. For
instance, if x = –4, then | x | = | –4 | = + 4 = –(–4) = –x. In fact,
for any negative value of x, the sign would have to be
changed, so:
• For x < 0, | x | = –x

14. • This is a case in which the "minus" sign on the variable does
not indicate "a number to the left of zero", but "a change of
the sign from whatever the sign originally was". This "–" does
not mean "the number is negative" but instead means that
"I've changed the sign on the original value".
• Must –x be negative? Why or why not?
• No, it does not have to be negative:
If the original value of x was negative, then –x, the opposite-
signed version of x, would have to be positive. For instance,
if I start with x = –3, then –x = –(–3) = +3, which is positive.