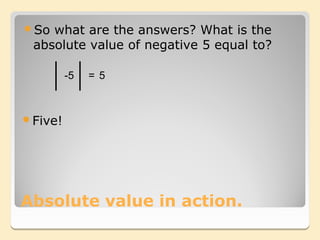The document discusses solving absolute value equations. It defines absolute value as the distance of a number from zero, which is never negative. To solve an absolute value equation, isolate the absolute value term and make two equations by changing the non-absolute value side to positive and negative values, yielding two solutions.

1. Solving Absolute Value
Equations

2. What does absolute value mean and why
is it important?
There is a technical definition for absolute
value, but you could easily never need it.
For now, you should view the absolute
value of a number as its distance from
zero.

3. 5
4
3
2
1
5
4 5
3 4
2 3
1 2
0– 1
Think of it as a number line…
Let's look at the number line:
– 5 – 4 – 3 – 2 – 1 0 1 2 3 4 5
The absolute value of x, is the distance of x from zero.
•This is why absolute value is never negative;
•Absolute value only asks "how far?", not "in which
direction?".
•This means not only that | 3 | = 3, because 3 is three units
to the right of zero, but also that | –3 | = 3, because –3 is
three units to the left of zero.

4. Absolute value has a symbol, actually
two, just like other operations.
 The symbols for absolute value are two vertical lines. They are
meant to surround the value that you want to take the absolute
value of, sort of like parenthesis surround the symbols that they
group.
The symbols

5. Here are two simple examples. Say that I
wanted to take the absolute value of -5. I
would write it like this:
-5
Thiswould be read in English as, “The
absolute value of negative 5.”
An example.

6. |-6| The absolute value of negative 6.
|10| The absolute value of 10.
|x| The absolute value of x.
|y| The absolute value of y.
|-y +2| The absolute value of negative y plus 2.
|0| The absolute value of 0.
We got it? Here’s a few more.

7. So what are the answers? What is the
absolute value of negative 5 equal to?
-5 = 5
Five!
Absolute value in action.

8.  It’s simple. Well, it’s a simple as this:
 If an input is positive, it STAYS positive.
 If an input is negative, it becomes positive.
 If an input is zero, it stay zero.
How it works for all numbers (inputs)

9. |-6| = 6.
|10| = 10. Note: NOT negative 10. Taking the absolute
value is NOT the same as taking the opposite.
|x| = x. But note, we still don’t know what x is.
|y| = y. y might be negative, positive, or zero.
|-y +2| This would have to be graphed. Y can be anything
and then we would shift the graph 2 to the right.
|0| = 0. The absolute value of 0 is 0. Period, end
of story.
Got it? Try to apply it.

10. Ok, we now know what absolute value
does, but if that’s a new concept to you
then practice it well. To reach the level of
the standard we have to move on.
First lets look at a simple equation and
solve it:
x + 10 = 293
-10 = -10 Subtract 10 from both sides.
x = 283 Solution x = 283.
 I hope that doesn’t shock anyone. If it does please go back and
review basic algebra. The rest of this will only confuse you if you
don’t.
Stay with me, there’s more.

11. Let’sadd absolute value into this same
equation:
|x + 10| = 293
This should be read: “The absolute value
of x + 10 equals 293.
Now we just saw that 283 is the answer
to this problem and I will tell you that it is
the ONLY solution. That is it is the only
replacement for x that makes the
statement x + 10 = 293 a true statement.
Now a little thinking.

12. With absolute value in the equation:
|x + 10| = 293
Let’s think. What if x + 10 came out to be
-293.
Then we would have |-293| = 293.
And that’s a true statement.
Another story

13. -303 + 10 equals = -293
So if x equaled -303 then the equation
would be true.
There are TWO solutions to the equation |
x + 10| = 293.
In fact there usually are two solutions to
an equation that involves absolute value.
Think even harder.

14. And I have good news and bad news.
The good news is that you don’t have to
GUESS every time you encounter an
absolute value problem.
The more good news is that there is a
systematic method for finding both
solutions.
The bad news is that you will have to
learn and memorize this method.
The good and the bad.

15.  Firstisolate the absolute value sign on one side:
 It has to read, “The absolute value of something,
equals something.”
 With our sample problem we’re already good.
 Now you have to change the right side of the
equation and get rid of the absolute value signs.
We are going to have two solutions and so we’re
going to have two equations.
|x + 10| = 293
We have:
x + 10 = 293 and: x + 10 = - 293
The method

16. That’s right we have:
x + 10 = 293 and: x + 10 = - 293
It may seem strange to change the right
side of the equation to find out what that
the variable is on the LEFT side, but trust
me it works.
Notice
that the absolute value signs are
now GONE. These two are easy to solve.
Seem strange?

17. x + 10 = 293
- 10 = - 10
x = 283
x + 10 = -293
- 10 = - 10
x = - 303
Two worked out solutions

18. We get two solutions.
x = 283 and: x = - 303
This
may seem strange but they both
make the original equation true. Watch…
| x + 10 | = 293
Plug in 293…..
|283 + 10| = 293
| 293 | = 293
 293 = 293 true
Seem strange?

19. | x + 10 | = 293
Plug in -303…
|-303 + 10| = 293
| -293 | = 293
 293 = 293 true
See? This one works too.
Now the other one.

20. Let’s review.
Remember. When the absolute value
signs get involved in an equation then you
can expect that there will be TWO
solutions and constructing TWO equations
is necessary to finding these solutions.
Isolatethe absolute value on one side of
the equation.
Make two versions of the equation. In one
make the NON-absolute value side
negative, in the other make it positive.