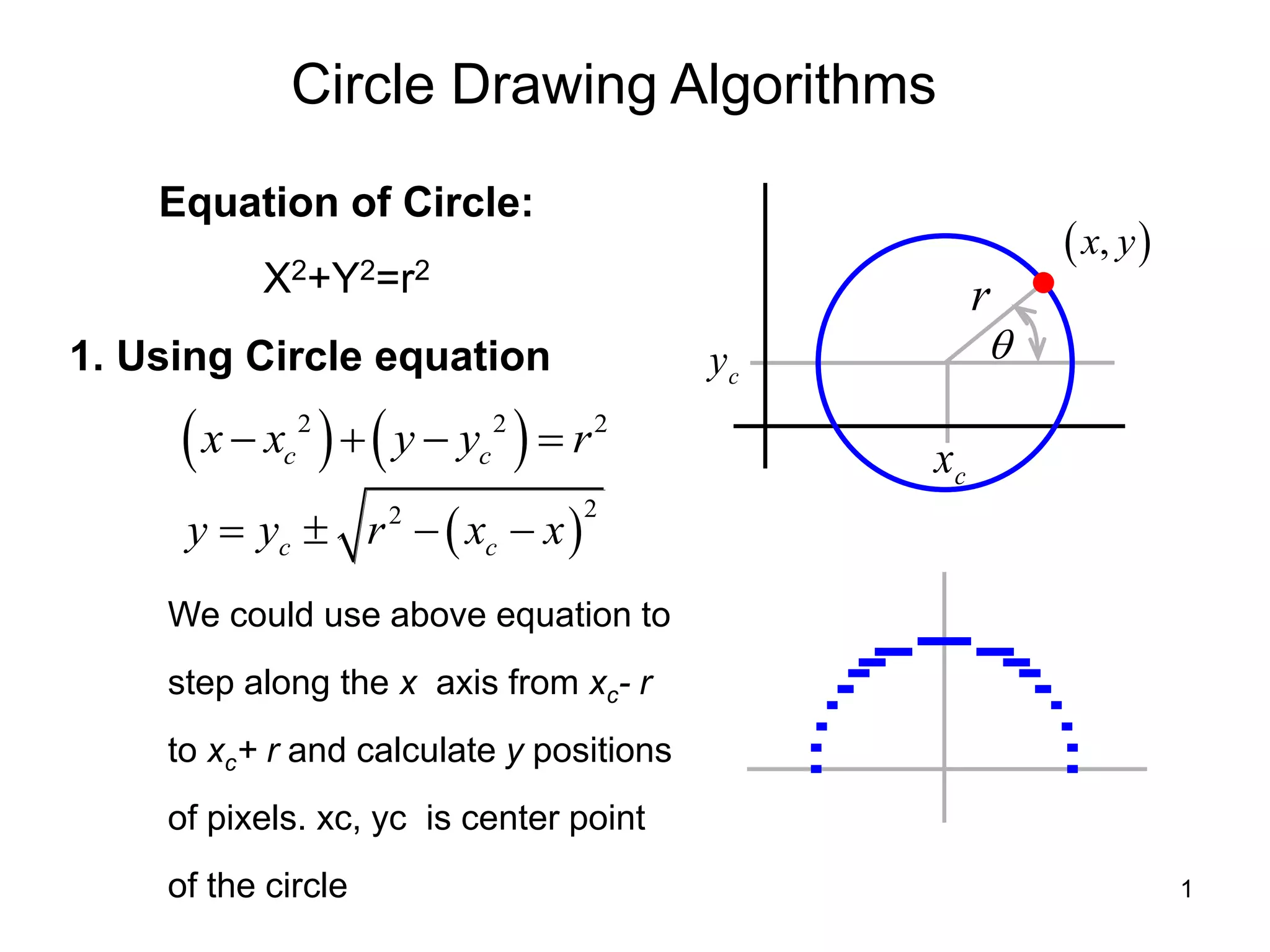
The document describes several algorithms for drawing circles: 1. Using the circle equation requires significant computation and results in a poor appearance. 2. Using trigonometric functions is time-consuming due to trig computations. 3. The midpoint circle algorithm uses the midpoint between candidate pixels to determine which is closer to the actual circle. It has less computation than the circle equation. 4. Bresenham's circle algorithm uses a decision parameter D to iteratively select the next pixel, requiring fewer computations than trigonometric functions.

1. 1
Circle Drawing Algorithms
 
,
x y

c
x
c
y
r
   
2 2 2
c c
x x y y r
   
We could use above equation to
step along the x axis from xc- r
to xc+ r and calculate y positions
of pixels. xc, yc is center point
of the circle
 
2
2
c c
y y r x x
   
1. Using Circle equation
Equation of Circle:
X2+Y2=r2

2. 2
DisAdv :
This requires considerable amount of computation (square root)
The drawing appearance is poor
Polar coordinates can be used with
uniform stepping of θ. This spaces
pixels evenly along circumference.
cos
sin
c
c
x x r
y y r


 
 
DisAdv:
Approach is time consuming due to trigonometric computations.
2. Using Trignometric Equation

3. 3
O
45
 
,
x y
 
,
x y

 
,
x y

 
,
x y
 
 
,
y x
  
,
y x
 
,
y x
   
,
y x

Any of the methods can use symmetry for efficiency. Circle
follows octant symmetry.
Calculate points for one octant; replicate in other seven
Plot (Y+Xc , X+Yc) ……Octant-1
Plot (X+Xc , Y+Yc) ……Octant-2
Plot (-X+Xc , Y+Yc) ……Octant-3
Plot (-Y+Xc , X+Yc) ……Octant-4
Plot (-Y+Xc , -X+Yc) ……Octant-5
Plot (-X+Xc , -Y+Yc) ……Octant-6
Plot (X+Xc , -Y+Yc) ……Octant-7
Plot (Y+Xc , -X+Yc) ……Octant-8

4.   2 2 2
circ ,
f x y x y r
  
k
y
1
k
y 
2
k
x 
1
k
x 
k
x
midpoint
2 2 2
0
x y r
  
3. Midpoint Circle Algorithm
Mid point determines the mid point between 2 pixels

5. 5
(xk+1, yk)
(xk+1, yk-1)
(xk, yk)
• Assume that we
just plotted point (xk, yk)
• The next point is a
choice between (xk+1, yk)
and (xk+1, yk-1)
• We would like to choose
the point that is nearest to
the actual circle
• So how do we make this choice?

6. 6
Mid-Point Circle Algorithm
• Let’s the equation of the circle slightly to give
us:
• The equation evaluates as follows:
• By evaluating this function at the midpoint
between the candidate pixels we can make
our decision
2
2
2
)
,
( r
y
x
y
x
fcirc 










,
0
,
0
,
0
)
,
( y
x
fcirc
boundary
circle
the
inside
is
)
,
(
if y
x
boundary
circle
on the
is
)
,
(
if y
x
boundary
circle
the
outside
is
)
,
(
if y
x

7. 7
 
   
Assuming that last plotted pixel was , , we need decide
whether next plotted is 1, or 1, 1 .
k k
k k k k
x y
x y x y
  
 
 
If 0 midpoint is inside the circle and pixel 1, is
closer to circle and plotted. Otherwise 1, 1 does.
k k k
k k
p x y
x y
 
 

8. 8
• Assuming we have just plotted the pixel at
(xp,yp) so we need to choose between
(xp+1,yp) and (xp+1,yp-1)
• Our decision variable can be defined as:
• If dk < 0 the midpoint is inside the circle and
the pixel at yp is closer to the circle
• Otherwise the midpoint is outside and yp-1
is closer
2
2
2
)
2
1
(
)
1
(
)
2
1
,
1
(
r
y
x
y
x
f
d
p
p
p
p
circ
k









9. March 2010 9
y
x
1 2 3 4 5 6 7 8 9
0 10
1
2
3
8
9
0
10
5
6
7
4
k pk (xk+1,yk+1) 2xk+1 2yk+1
0 - 9 (1,10) 2 20
1 - 6 (2,10) 4 20
2 - 1 (3,10) 6 20
3 6 (4,9) 8 18
4 - 3 (5,9) 10 18
5 8 (6,8) 12 16
6 5 (7,7) 14 14
0 0 0
Example: Draw a circle with 10.
Initialization: 1 10 9 ; 2 0 , 2 20
r
p x y

     

10. 10
Mid Point algorithm
Step 1: Given (xc,yc) and r
Step 2: set x=0, y=r d=5/4 –r OR d=1-r
Step 3: WHILE (x<y)
xnext =xlast +1
Ynext =ylast (d<0) OR ylast -1 (d>0)
d=d+2 (xnext) =1 (d<0)
d=d+2 (xnext - ynext)+1 (d>0)
OR following algorithm is also correct where yk is xlast and yk+1 is ynext

11. 11
Step 1: Get the Radius of Circle R
And Coordinates of centre of circle (Xc,Yc).
Step 2: X and Y are going to be plotted points
Set X=0 and Y=R
Step 3: D = 3-2R (Initial decision Parameter)
Step 4: Plot Circle (Xc,Yc,X,Y)
Step 5: if D < 0 Then
D = D + 4X + 6
X=X+1
Y=Y
Else
D=D+4(X-Y)+10
X=X+1
Y=Y-1
Step 6: Check, if X=Y
Goto Step 7
Else
Goto Step 4
4. Bresenham’s Circle Algorithm