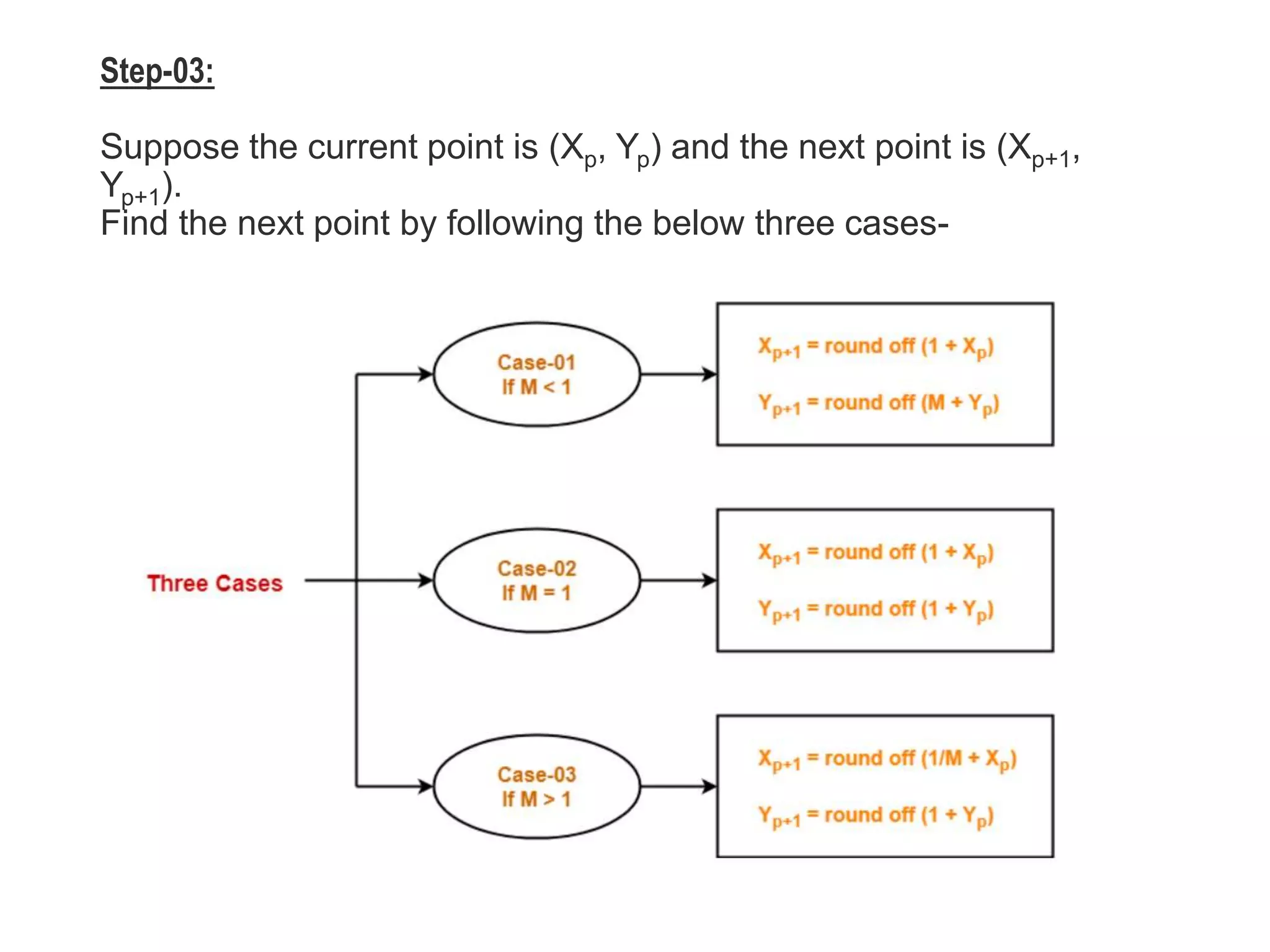
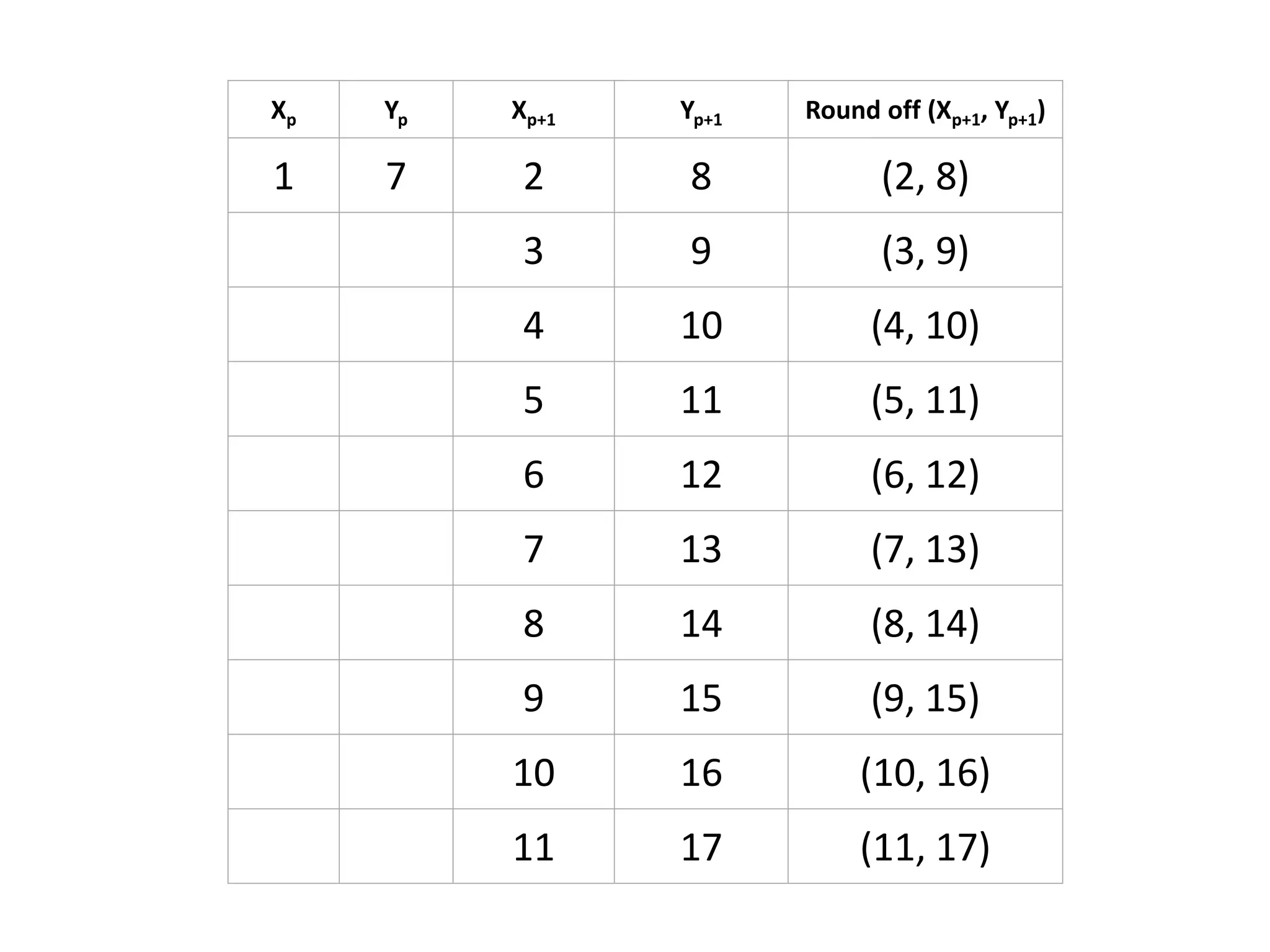
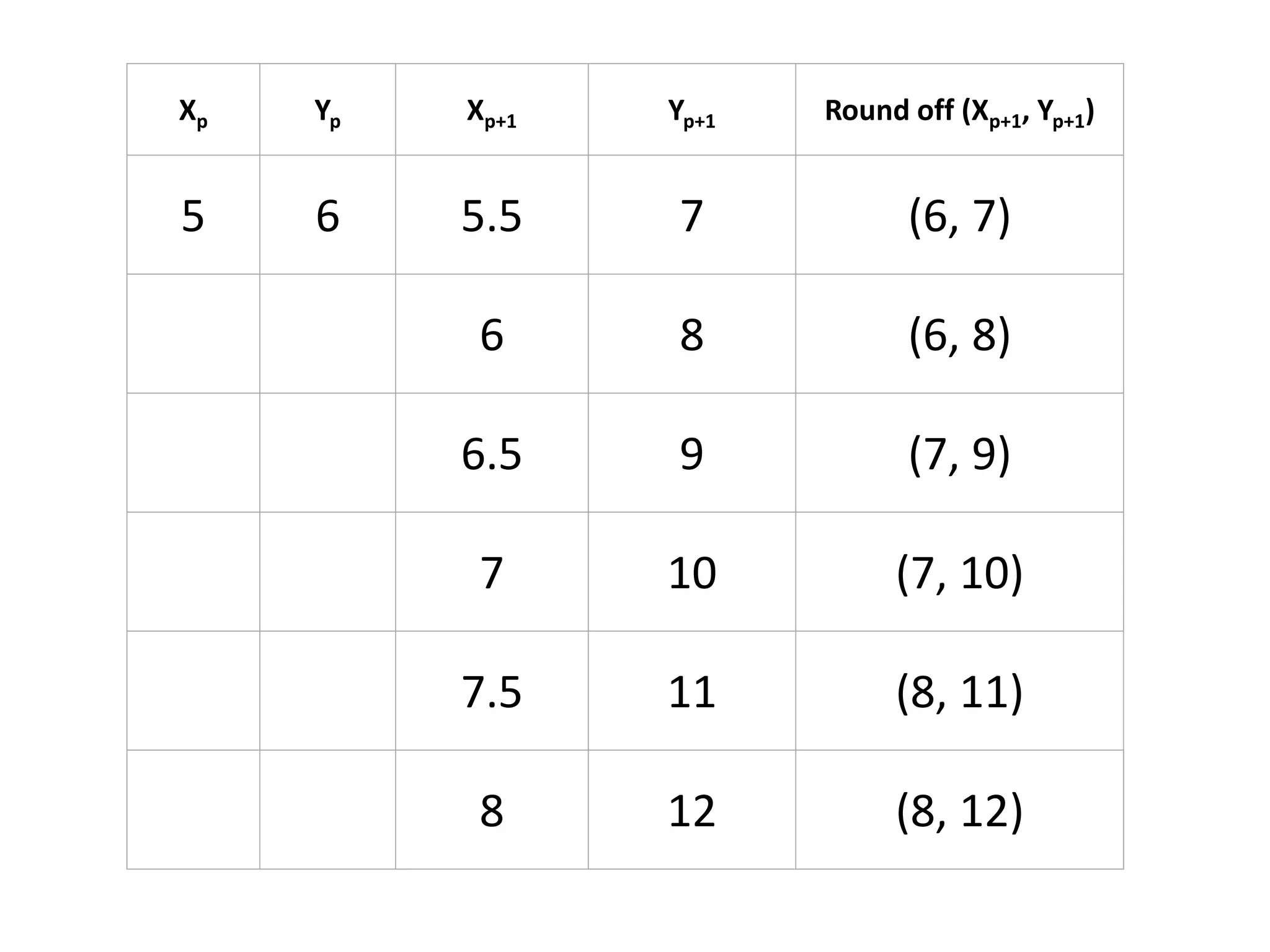
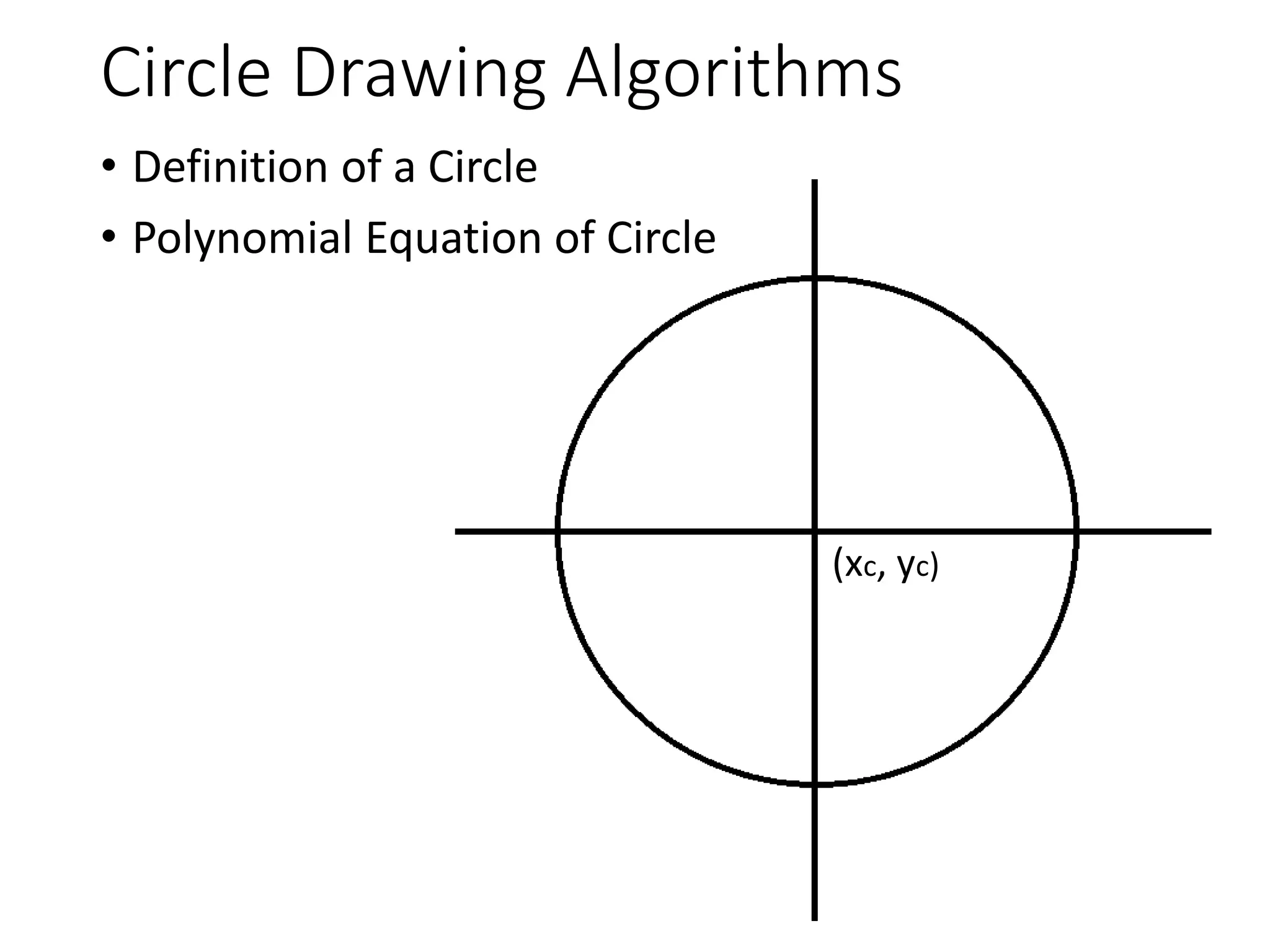
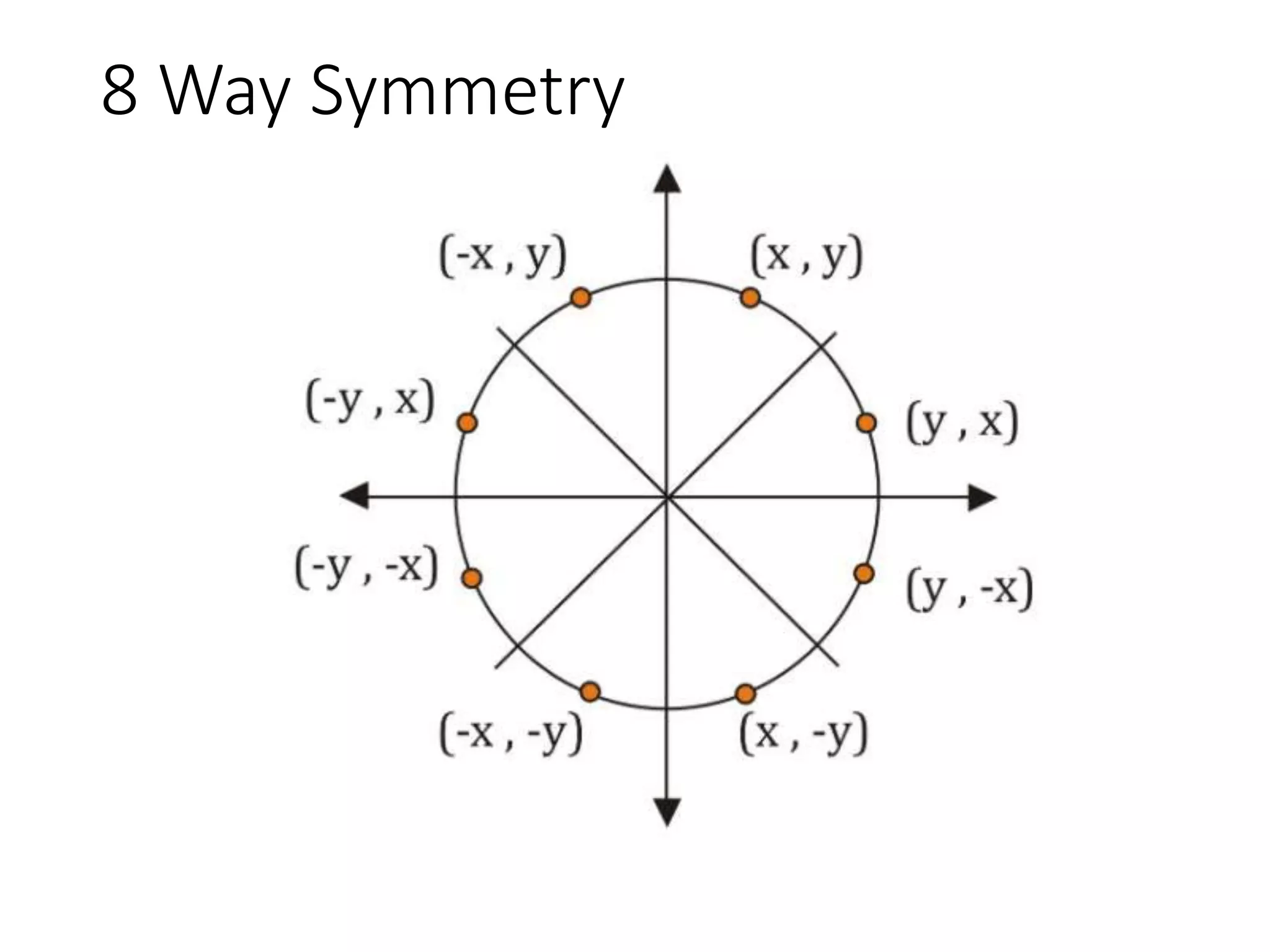
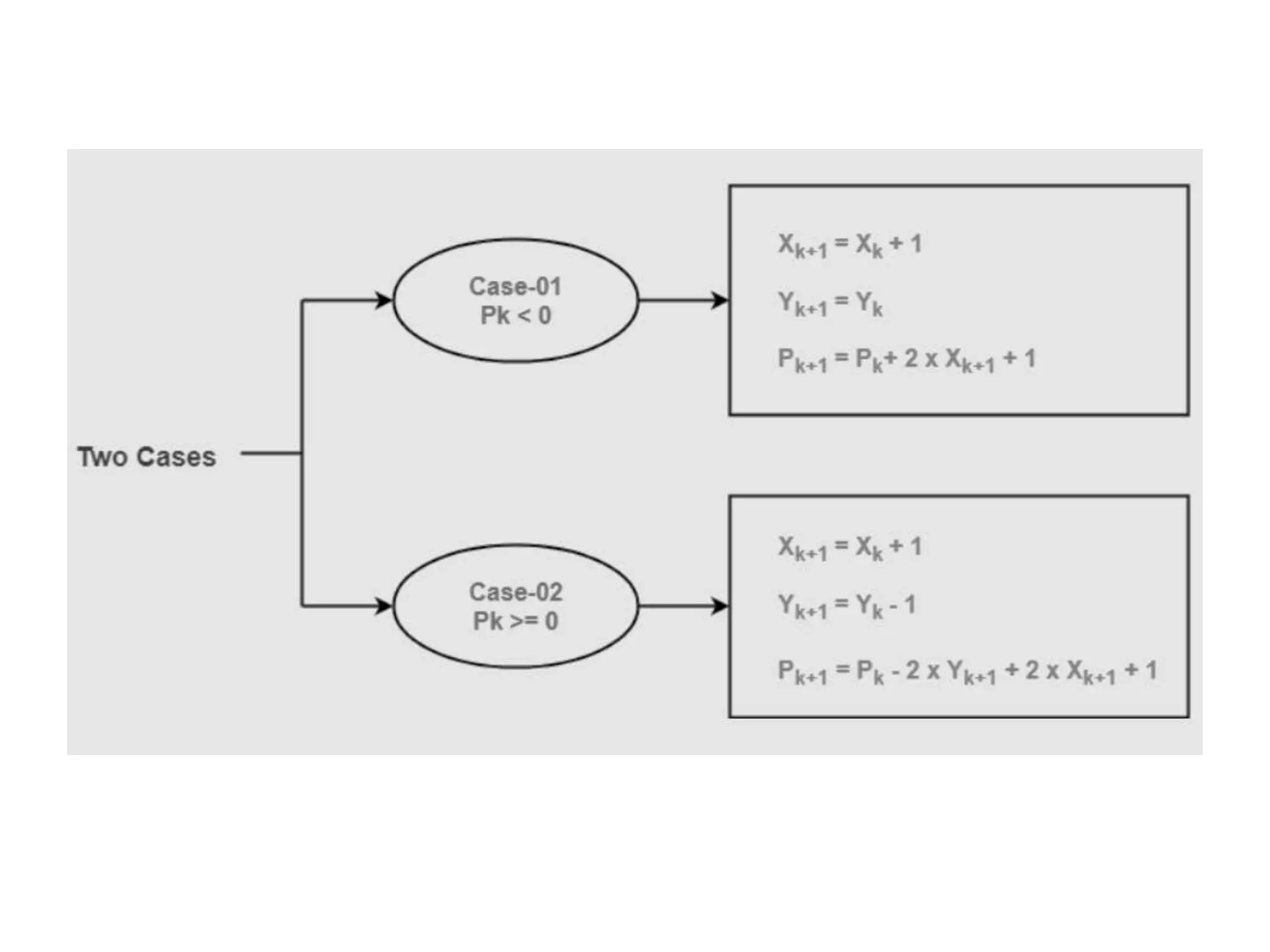
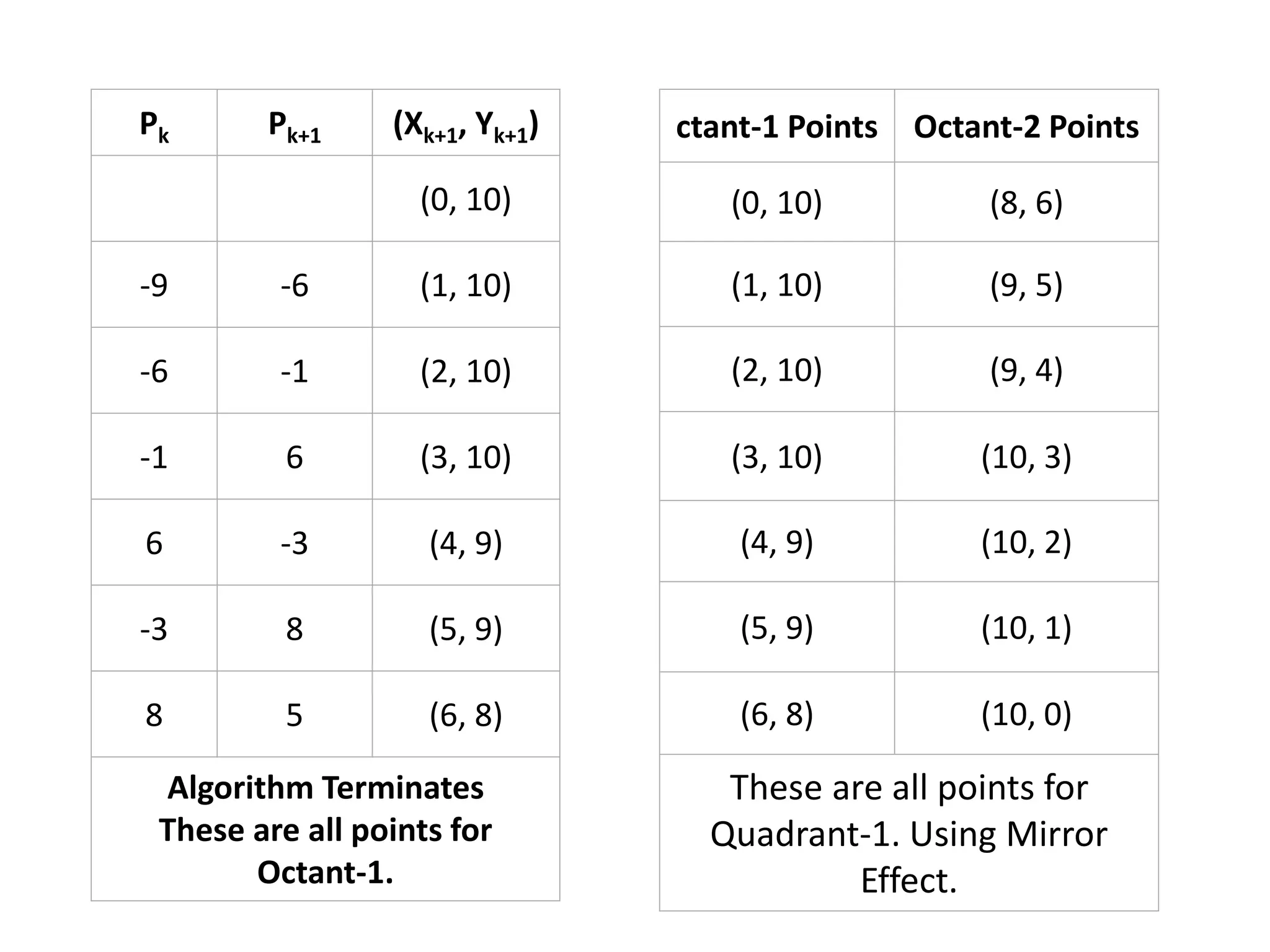
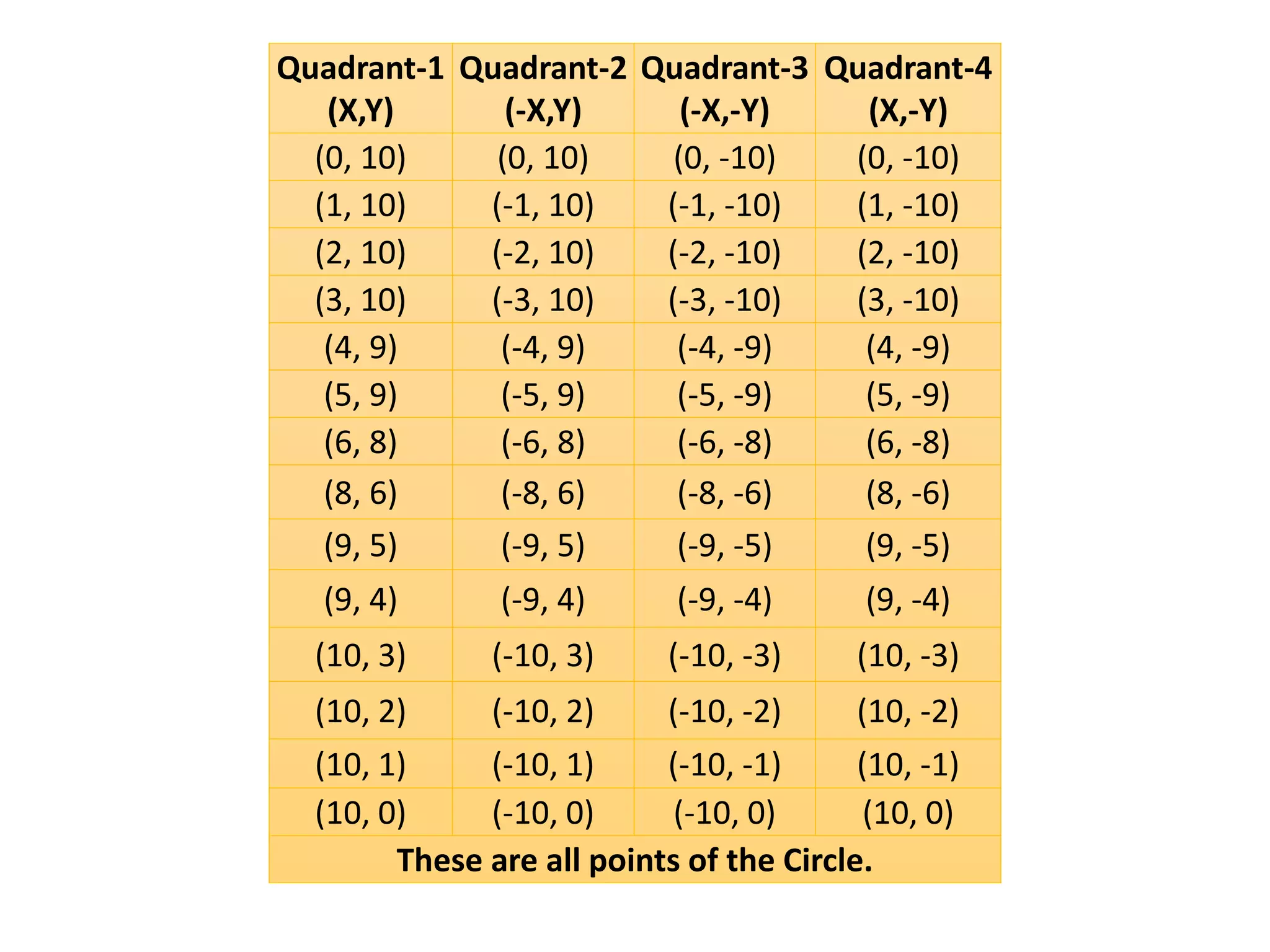
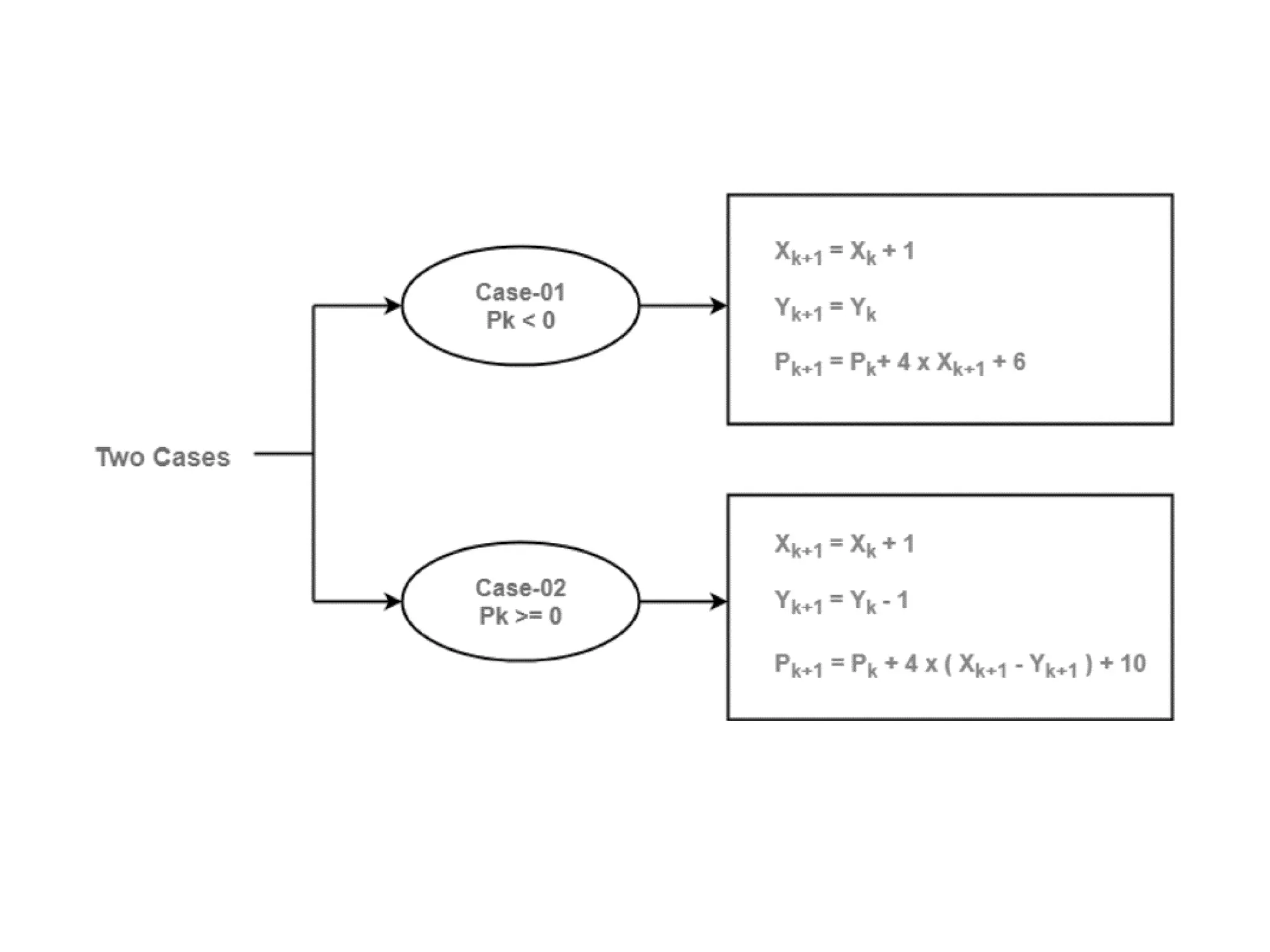
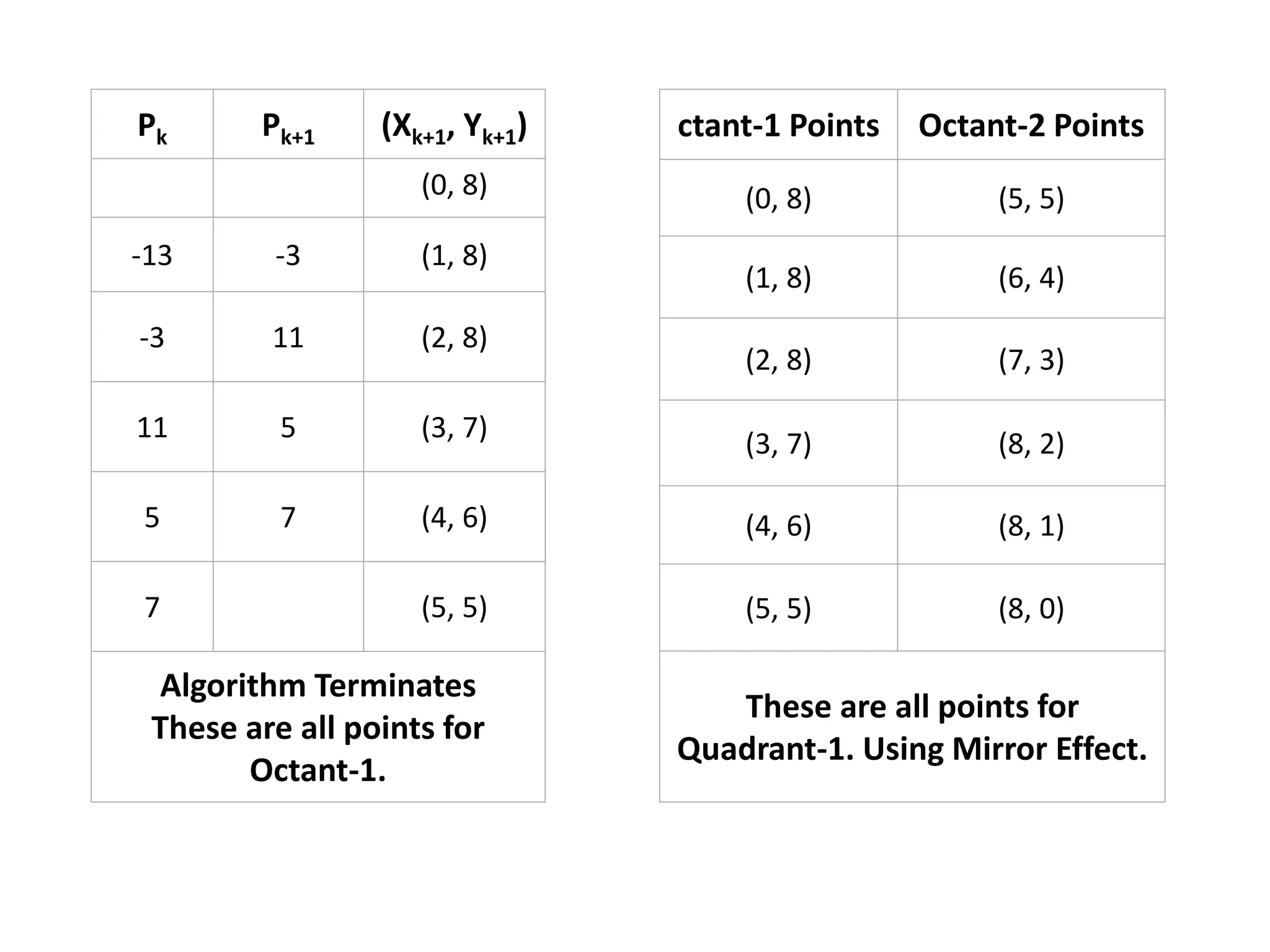
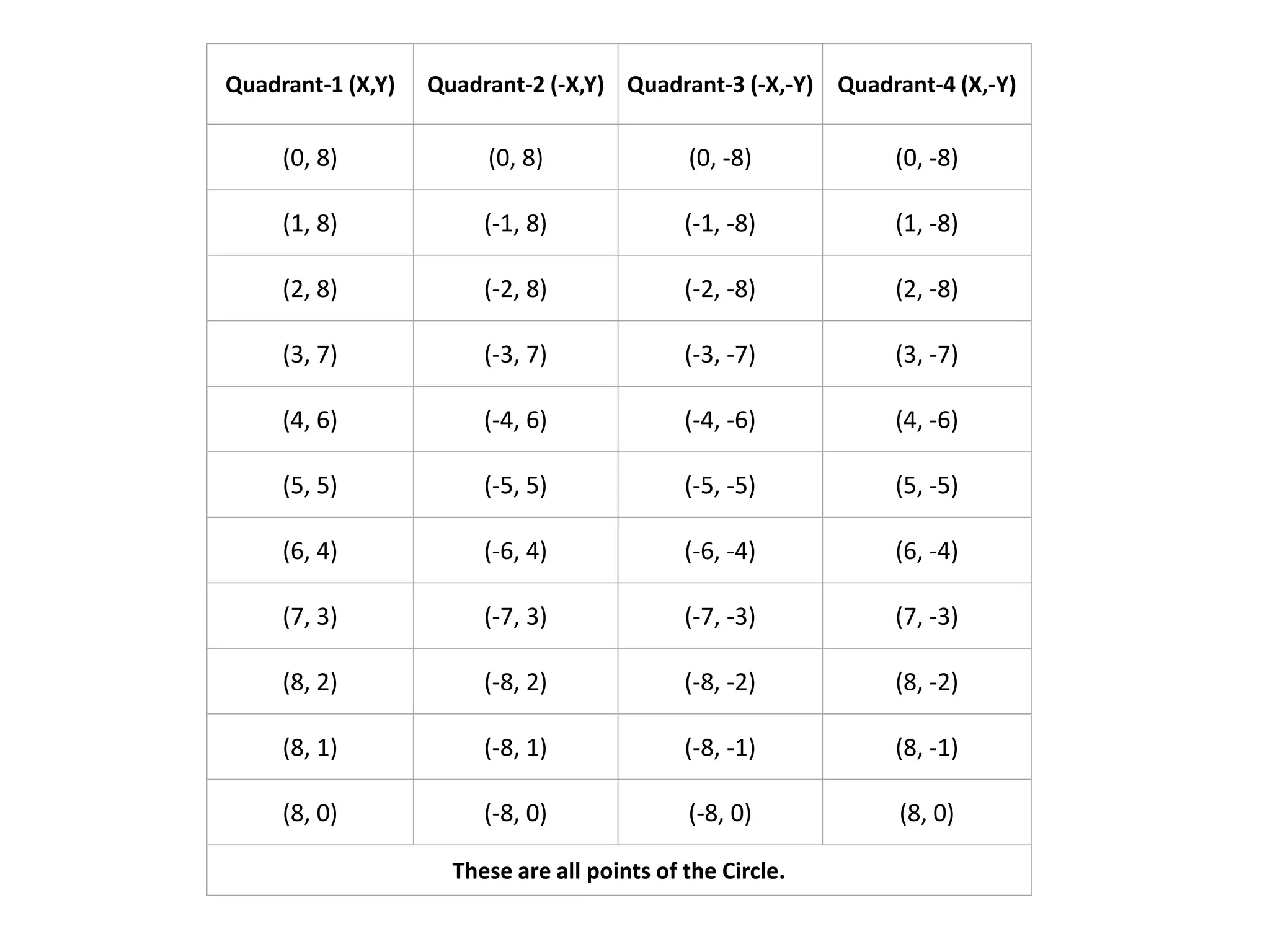
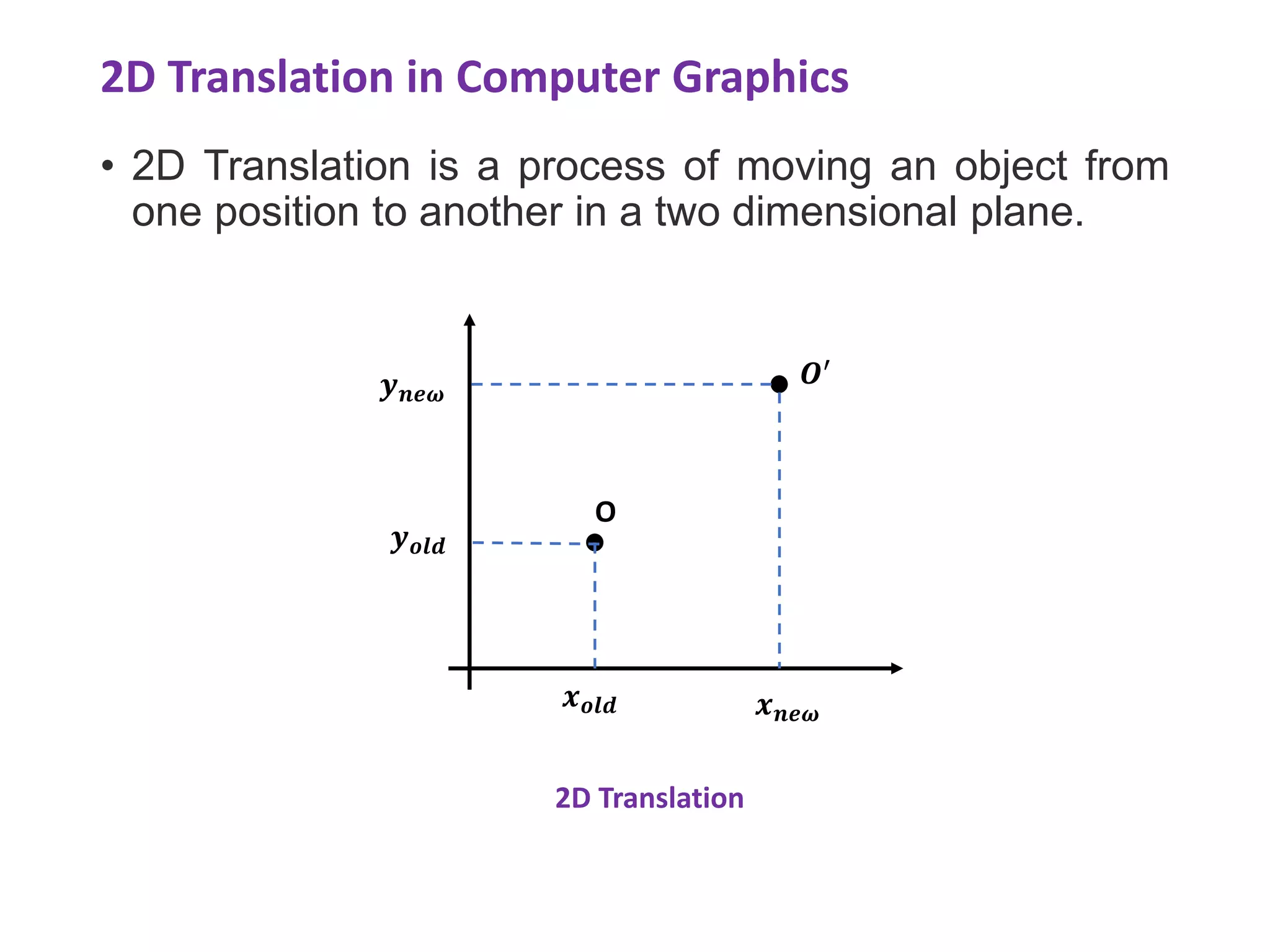
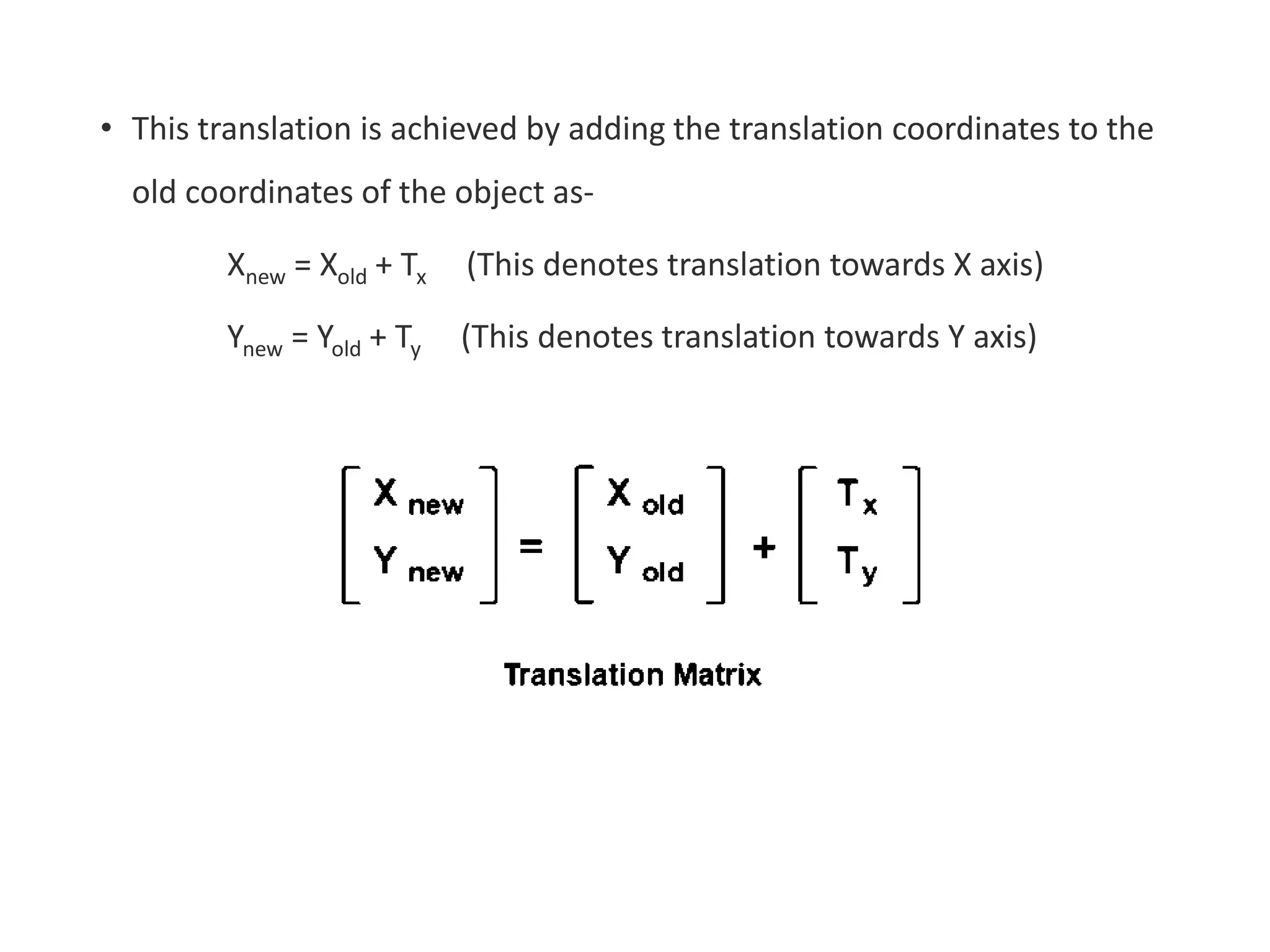
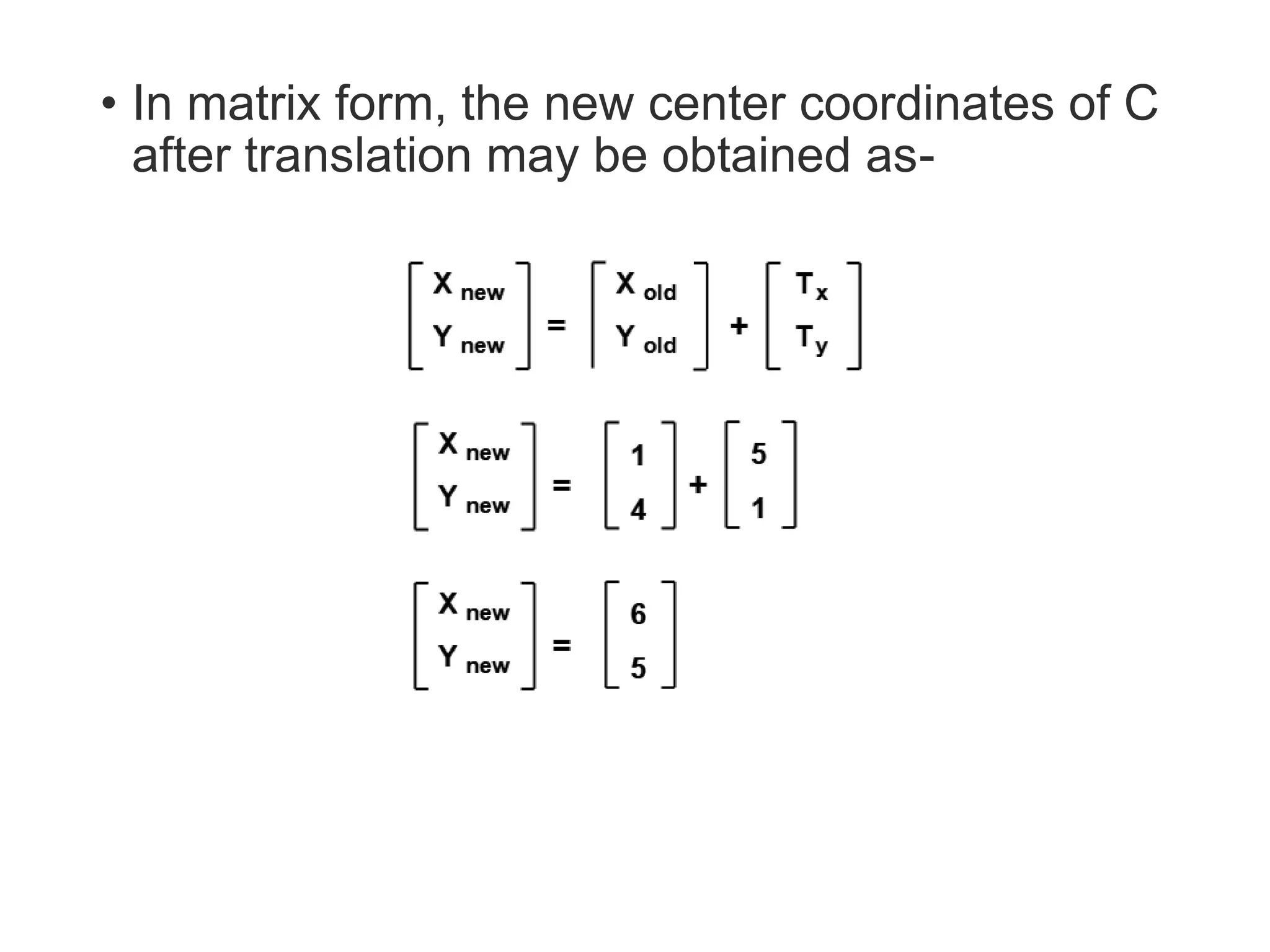
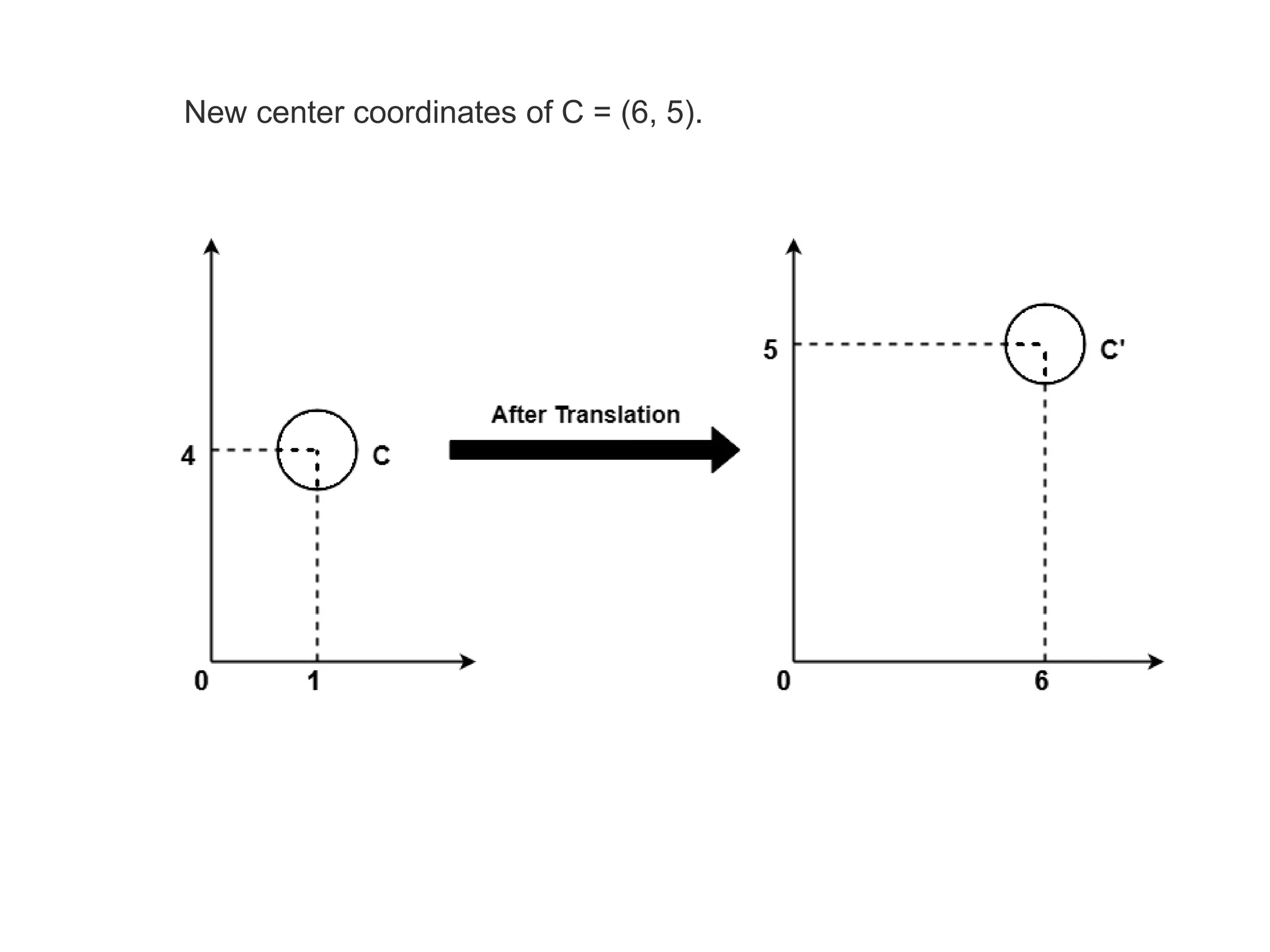
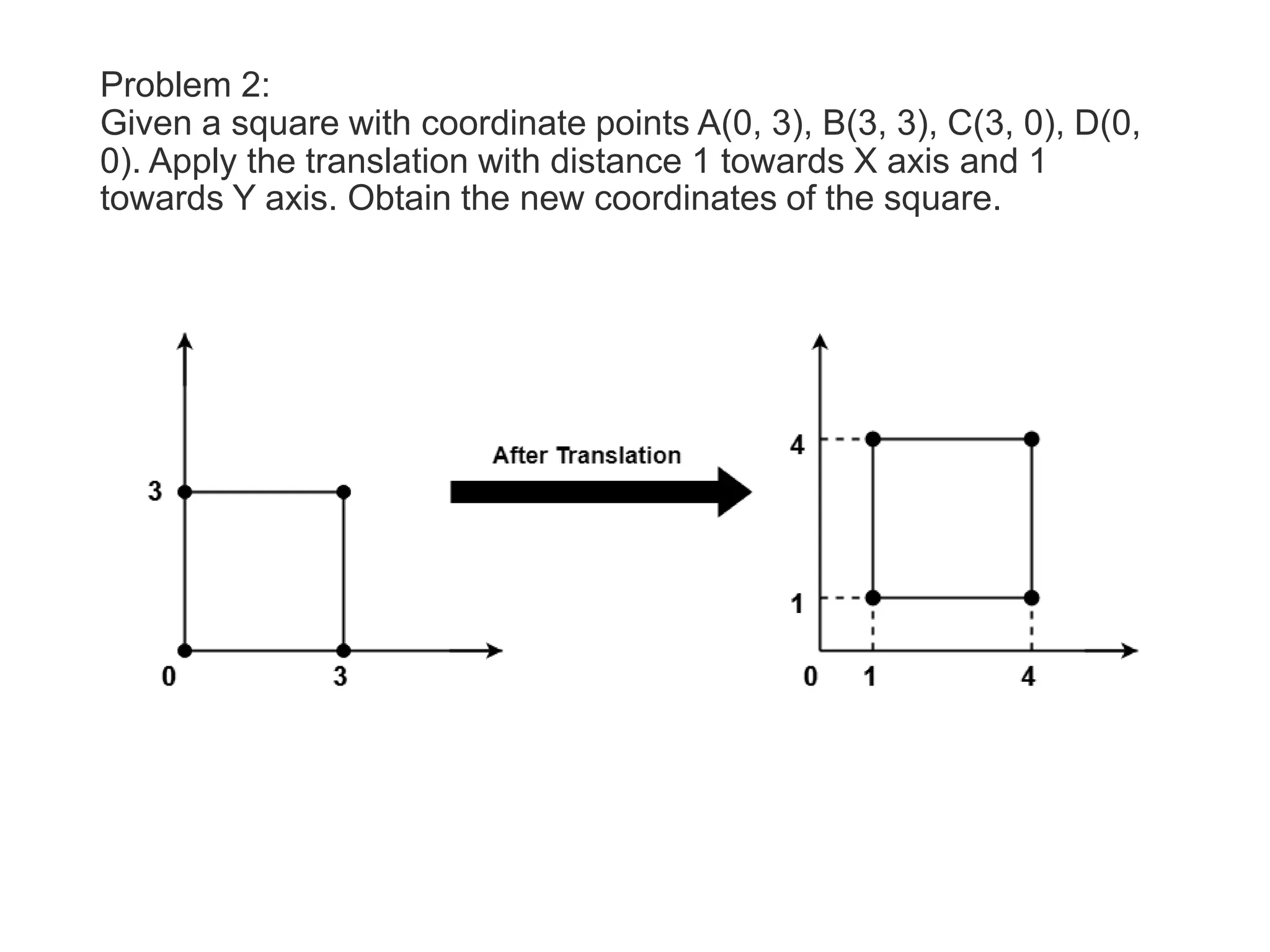
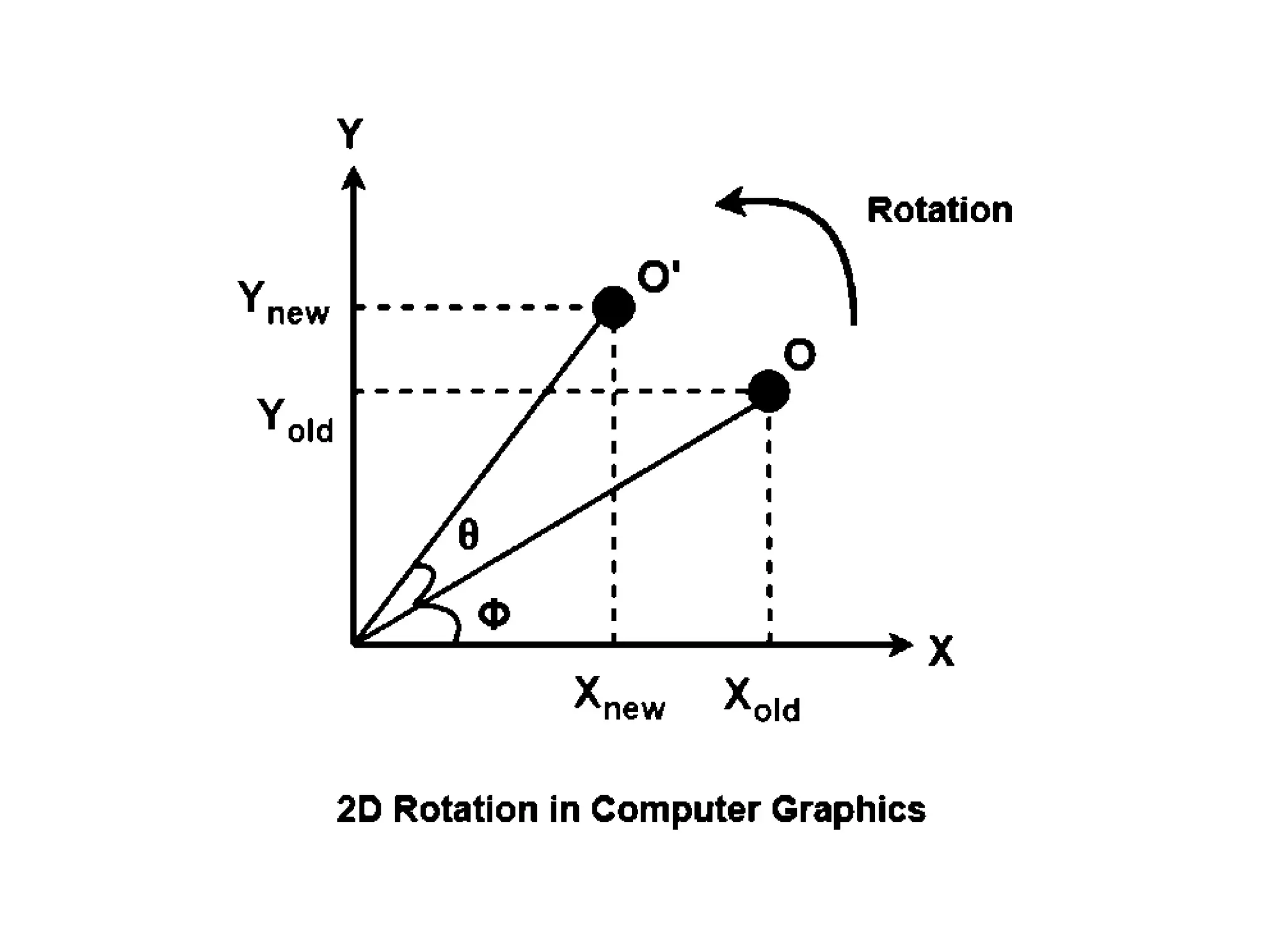
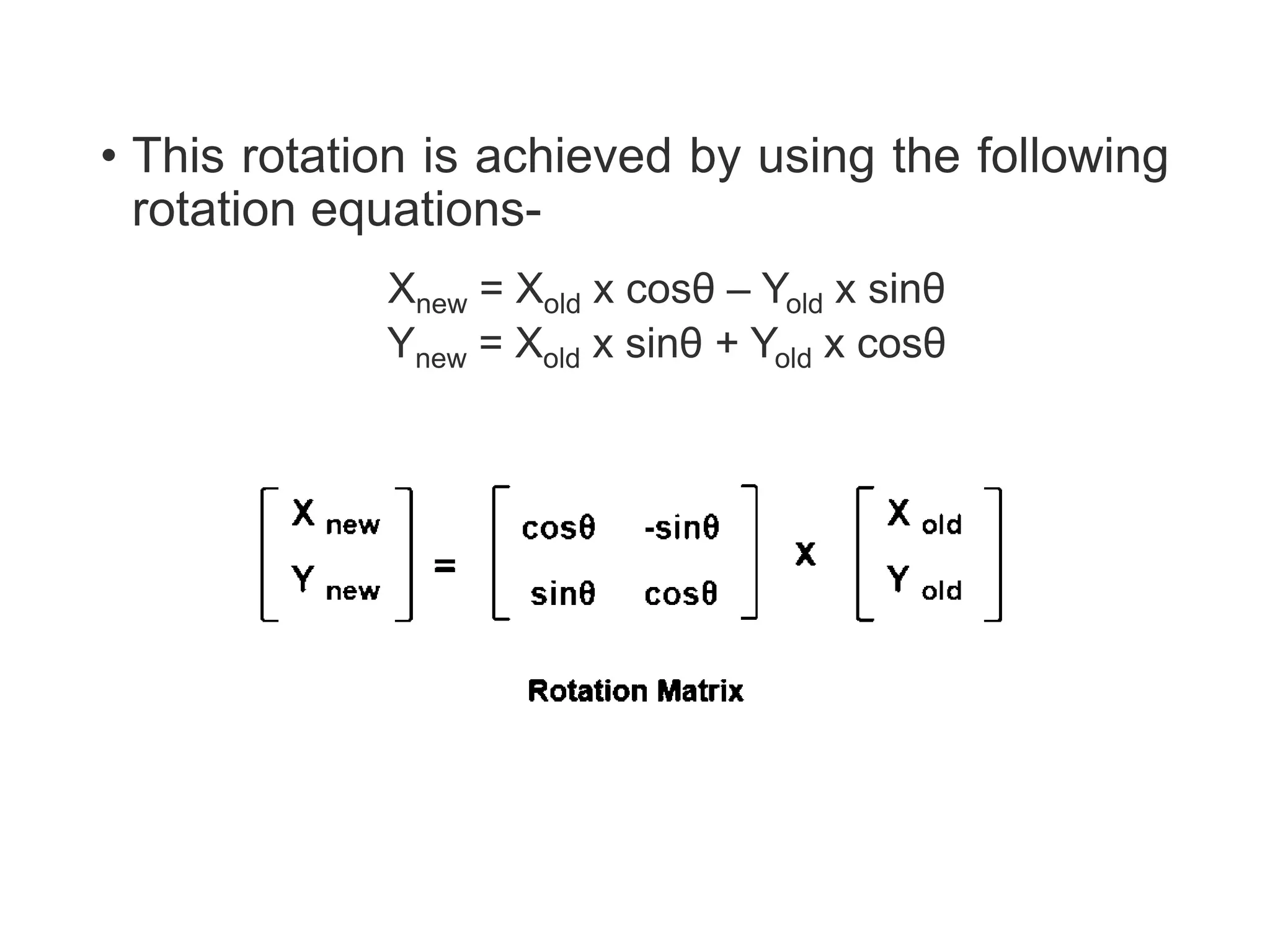
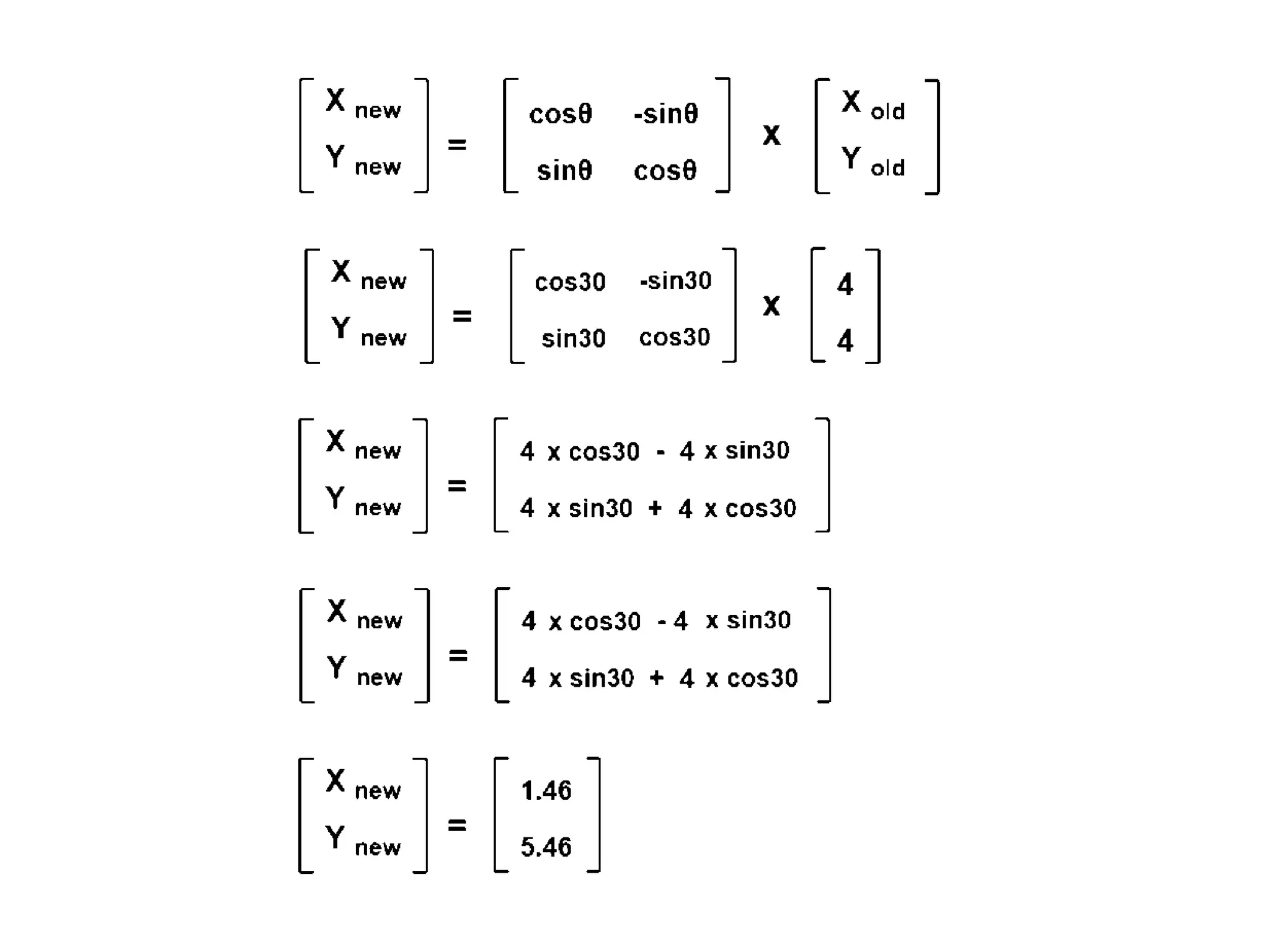
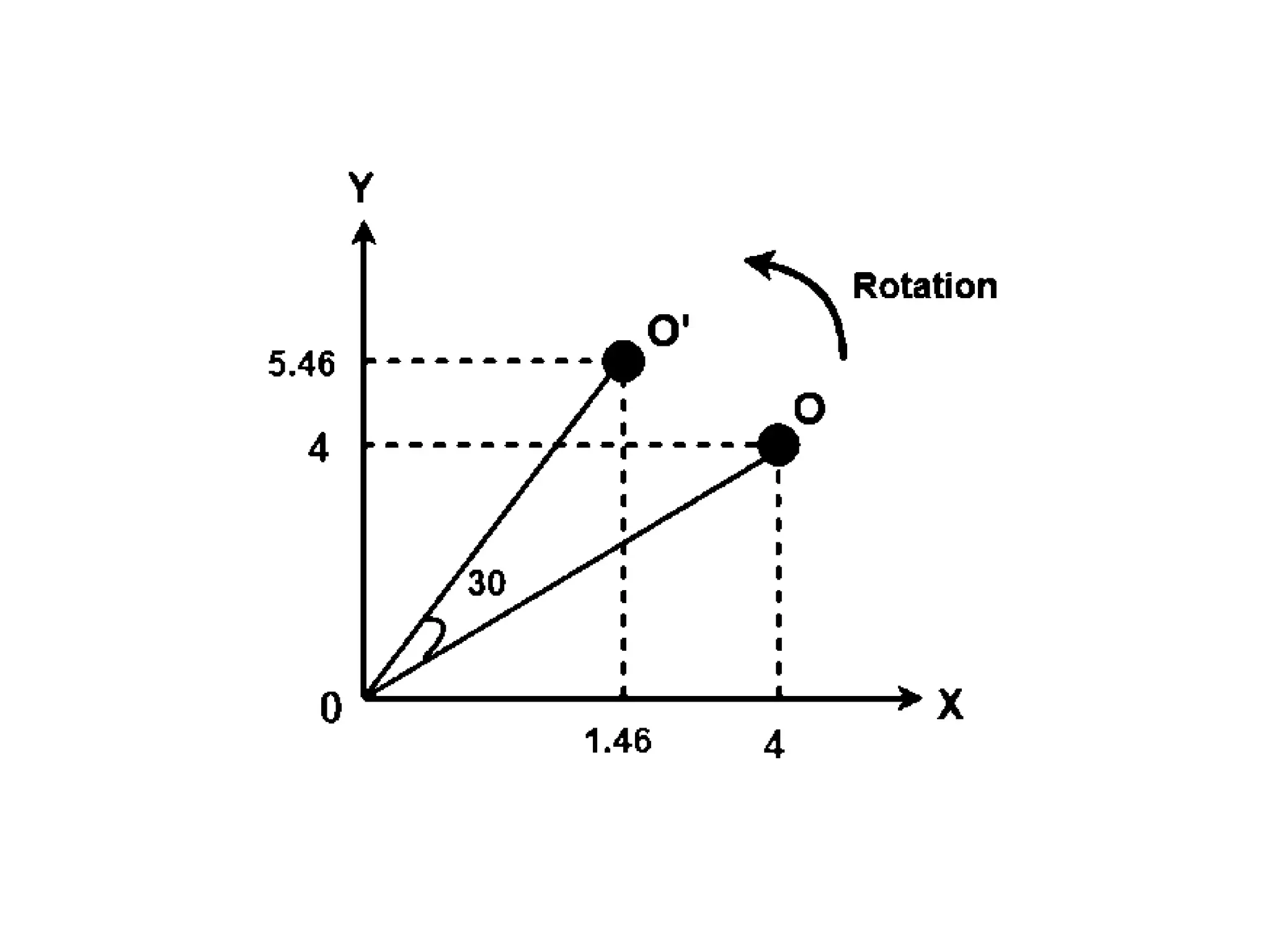
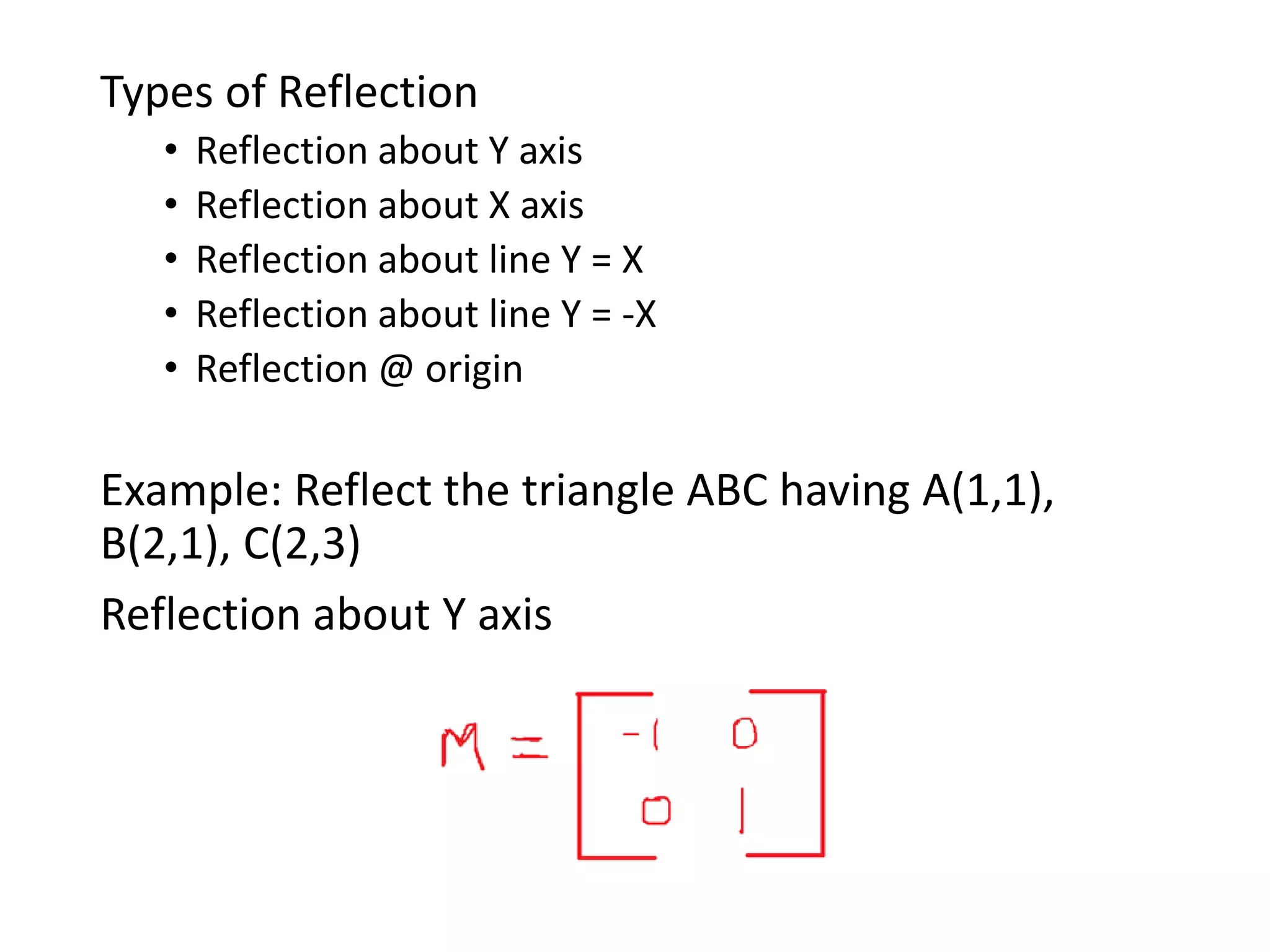
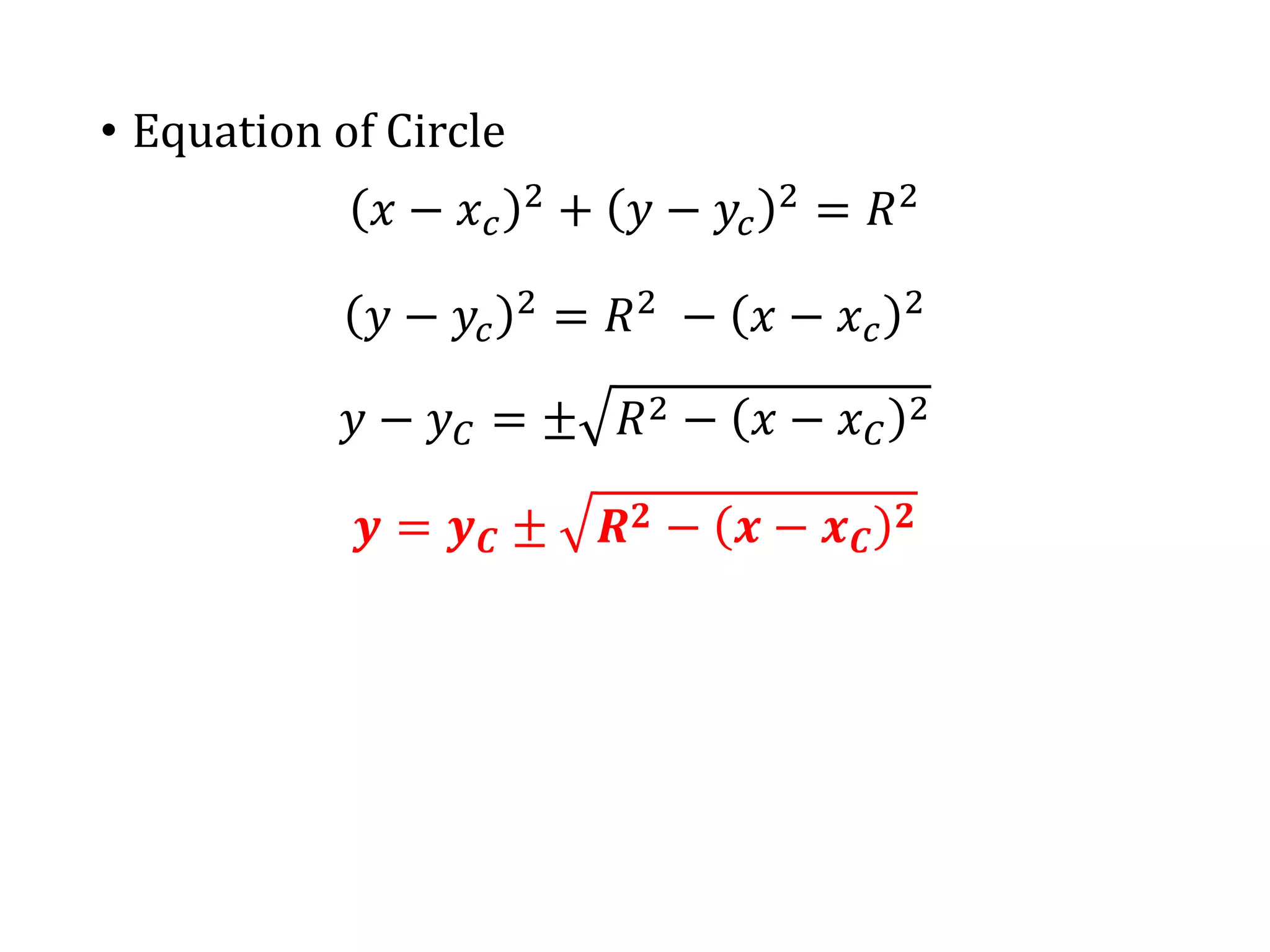The document describes the Digital Differential Analyser (DDA) algorithm for generating points on a line between two given points. It provides the step-by-step procedure which includes calculating the change in x and y between points, determining the step size, calculating the increment amounts, and using a for loop to generate each point by incrementing x and y at each step. Examples are given to demonstrate calculating points between two given start and end points.

1. Digital Differential
Analyser

2. Procedure
Calculate dx= x2-x1 and dy= y2-y1
If(abs(dx)>abs(dy))
step= abs(dx)
else
step= abs(dy)
xinc = dx/step
yinc = dy/step
for(i=1; i<=step; i++)
{
putpixel(x1, y1);
x1 = x1 + xinc;
y1 = y1 + yinc;
}

3. Digital Differential Analyser
• Procedure-
• Given-
• Starting coordinates = (X0, Y0)
• Ending coordinates = (Xn, Yn)
• The points generation using DDA Algorithm involves the following
steps-
• Step-01:
Calculate ΔX, ΔY and M from the given input.
These parameters are calculated as-
• ΔX = Xn – X0
• ΔY =Yn – Y0
• M = ΔY / ΔX

4. • Step-02:
• Find the number of steps or points in between
the starting and ending coordinates.
• if (absolute (ΔX) > absolute (ΔY))
Steps = absolute (ΔX);
else
Steps = absolute (ΔY);

5. Step-03:
Suppose the current point is (Xp, Yp) and the next point is (Xp+1,
Yp+1).
Find the next point by following the below three cases-

6. • Problem-01:
• Calculate the points between the starting point (1, 7) and
ending point (11, 17).
Solution-
• Given-
• Starting coordinates = (X0, Y0) = (1, 7)
• Ending coordinates = (Xn, Yn) = (11, 17)
• Step-01:
• Calculate ΔX, ΔY and M from the given input.
• ΔX = Xn – X0 = 11 – 1 = 10
• ΔY =Yn – Y0 = 17 – 7 = 10
• M = ΔY / ΔX = 10 / 10 = 1
• Step-02:
• Calculate the number of steps.
• As |ΔX| = |ΔY| = 10 = 10, so number of steps = ΔX = ΔY = 10
• Step-03:
• As M = 1, so case-02 is satisfied.
• Now, Step-03 is executed until Step-04 is satisfied.

7. Xp Yp Xp+1 Yp+1 Round off (Xp+1, Yp+1)
1 7 2 8 (2, 8)
3 9 (3, 9)
4 10 (4, 10)
5 11 (5, 11)
6 12 (6, 12)
7 13 (7, 13)
8 14 (8, 14)
9 15 (9, 15)
10 16 (10, 16)
11 17 (11, 17)

8. Problem-02:
Calculate the points between the starting point (5, 6) and ending point (8, 12).
Solution-
Given-
Starting coordinates = (X0, Y0) = (5, 6)
Ending coordinates = (Xn, Yn) = (8, 12)
Step-01:
Calculate ΔX, ΔY and M from the given input.
ΔX = Xn – X0 = 8 – 5 = 3
ΔY =Yn – Y0 = 12 – 6 = 6
M = ΔY / ΔX = 6 / 3 = 2
Step-02:
Calculate the number of steps.
As |ΔX| < |ΔY| = 3 < 6, so number of steps = ΔY = 6
Step-03:
As M > 1, so case-03 is satisfied.
Now, Step-03 is executed until Step-04 is satisfied.

9. Xp Yp Xp+1 Yp+1 Round off (Xp+1, Yp+1)
5 6 5.5 7 (6, 7)
6 8 (6, 8)
6.5 9 (7, 9)
7 10 (7, 10)
7.5 11 (8, 11)
8 12 (8, 12)

10. Solve the following
• Calculate the points between the starting point (5, 6)
and ending point (13, 10).

11. Advantages of DDA Algorithm-
• It is a simple algorithm.
• It is easy to implement.
• It avoids using the multiplication operation
which is costly in terms of time complexity.

12. Disadvantages of DDA Algorithm-
The disadvantages of DDA Algorithm are-
•There is an extra overhead of using round off(
) function.
•Using round off( ) function increases time
complexity of the algorithm.
•Resulted lines are not smooth because of
round off( ) function.
•The points generated by this algorithm are not
accurate.

13. Bresenham Line Drawing Algorithm
• Given-
Starting coordinates = (X0, Y0)
Ending coordinates = (Xn, Yn)
• The points generation using Bresenham Line Drawing Algorithm
involves the following steps-
• Step-01:
• Calculate ΔX and ΔY from the given input.
• These parameters are calculated as-
ΔX = Xn – X0
ΔY =Yn – Y0
• Step-02:
• Calculate the decision parameter Pk.
It is calculated as- Pk = 2ΔY – ΔX

14. • Step-03:
• Suppose the current point is (Xk , Yk) and the next point is (Xk+1 , Yk+1)
• Find the next point depending on the value of decision parameter Pk.
• Follow the below two cases-

15. • Step-04:
• Keep repeating Step-03 until the end point is reached or number of iterations
equals to (ΔX-1) times.
Problem No. 1
Calculate the points between the starting coordinates (9, 18) and ending
coordinates (14, 22)
Problem No. 2
Calculate the points between the starting
coordinates (20, 10) and ending coordinates (30, 18)

16. Circle Drawing Algorithms
• Definition of a Circle
• Polynomial Equation of Circle
(xc, yc)

17. Algorithms
• Direct Scan Conversion
• Mid Point Circle Drawing Algorithm
• Bresenhams Algorithm

19. • Equation of Circle
𝑥 − 𝑥𝑐
2
+ 𝑦 − 𝑦𝑐
2
= 𝑅2
𝑦 − 𝑦𝑐
2 = 𝑅2 − 𝑥 − 𝑥𝑐
2
𝑦 − 𝑦𝐶 = ± 𝑅2 − 𝑥 − 𝑥𝐶
2
𝒚 = 𝒚𝑪 ± 𝑹𝟐 − 𝒙 − 𝒙𝑪
𝟐

20. Algorithm

21. 8 Way Symmetry

22. Important Points
• Circle drawing algorithms take the advantage of 8
symmetry property of circle.
• Every circle has 8 octants and the circle drawing
algorithm generates all the points for one octant.
• The points for other 7 octants are generated by
changing the sign towards X and Y coordinates.
• To take the advantage of 8 symmetry property, the
circle must be formed assuming that the center point
coordinates is (0, 0).
• If the center coordinates are other than (0, 0), then we
add the X and Y coordinate values with each point of
circle with the coordinate values generated by
assuming (0, 0) as center point.

23. Mid Point Circle Drawing Algorithm
• Given the center point and radius of circle,
• Mid Point Circle Drawing Algorithm attempts to generate the
points of one octant.
• Procedure-
Given-
Centre point of Circle = (X0, Y0)
Radius of Circle = R
• The points generation using Mid Point Circle Drawing Algorithm
involves the following steps-
Step-01:
• Assign the starting point coordinates (X0, Y0) as-
• X0 = 0
• Y0 = R

24. Step-02:
• Calculate the value of initial decision parameter P0 as-
P0 = 1 – R
• Suppose the current point is (Xk, Yk) and the next point is (Xk+1,
Yk+1).
• E.g. if current point is (x1, y1) and next point is (x2,y2)
• Find the next point of the first octant depending on the value of
decision parameter Pk.
• There are two cases of decision parameter
• Case 1 – Pk < 0
• Case 2 - Pk >=0

26. Step-04:
• If the given centre point (X0, Y0) is not (0, 0), then do the following and plot the
point-
Xplot = Xc + X0
Yplot = Yc + Y0
• Here, (Xc, Yc) denotes the current value of X and Y coordinates.
Step-05:
• Keep repeating Step-03 and Step-04 until Xplot >= Yplot.
Step-06:
• Step-05 generates all the points for one octant.
• To find the points for other seven octants, follow the eight symmetry property
of circle.

27. Problem-01: Given the center point coordinates (0, 0)
and radius as 10, generate all the points to form a circle.
Solution-
Given-
Centre Coordinates of Circle (X0, Y0) = (0, 0)
Radius of Circle = 10
Step-01:
Assign the starting point coordinates (X0, Y0) as-
X0 = 0
Y0 = R = 10
Step-02:
• Calculate the value of initial decision parameter P0 as-
P0 = 1 – R
P0 = 1 – 10
P0 = -9

28. Step-03:
• As Pinitial < 0, so case-01 is satisfied.
Thus,
Xk+1 = Xk + 1 = 0 + 1 = 1
Yk+1 = Yk = 10
Pk+1 = Pk + 2 x Xk+1 + 1 = -9 + (2 x 1) + 1 = -6
Step-04:
• This step is not applicable here as the given center point
coordinates is (0, 0).
Step-05:
• Step-03 is executed similarly until Xk+1 >= Yk+1 as follows-

29. Pk Pk+1 (Xk+1, Yk+1)
(0, 10)
-9 -6 (1, 10)
-6 -1 (2, 10)
-1 6 (3, 10)
6 -3 (4, 9)
-3 8 (5, 9)
8 5 (6, 8)
Algorithm Terminates
These are all points for
Octant-1.
ctant-1 Points Octant-2 Points
(0, 10) (8, 6)
(1, 10) (9, 5)
(2, 10) (9, 4)
(3, 10) (10, 3)
(4, 9) (10, 2)
(5, 9) (10, 1)
(6, 8) (10, 0)
These are all points for
Quadrant-1. Using Mirror
Effect.

30. Quadrant-1
(X,Y)
Quadrant-2
(-X,Y)
Quadrant-3
(-X,-Y)
Quadrant-4
(X,-Y)
(0, 10) (0, 10) (0, -10) (0, -10)
(1, 10) (-1, 10) (-1, -10) (1, -10)
(2, 10) (-2, 10) (-2, -10) (2, -10)
(3, 10) (-3, 10) (-3, -10) (3, -10)
(4, 9) (-4, 9) (-4, -9) (4, -9)
(5, 9) (-5, 9) (-5, -9) (5, -9)
(6, 8) (-6, 8) (-6, -8) (6, -8)
(8, 6) (-8, 6) (-8, -6) (8, -6)
(9, 5) (-9, 5) (-9, -5) (9, -5)
(9, 4) (-9, 4) (-9, -4) (9, -4)
(10, 3) (-10, 3) (-10, -3) (10, -3)
(10, 2) (-10, 2) (-10, -2) (10, -2)
(10, 1) (-10, 1) (-10, -1) (10, -1)
(10, 0) (-10, 0) (-10, 0) (10, 0)
These are all points of the Circle.

31. Problem-02:
Given the center point coordinates (4, 4) and radius as
10, generate all the points to form a circle.

32. Bresenham Circle Drawing Algorithm
• Given the center point and radius of circle,
• Mid Point Circle Drawing Algorithm attempts to generate the
points of one octant.
• Procedure-
Given-
Centre point of Circle = (Xc, Yc)
Radius of Circle = R
• The points generation using Mid Point Circle Drawing Algorithm
involves the following steps-
Step-01:
• Assign the starting point coordinates (X0, Y0) as-
• X0 = 0
• Y0 = R

33. Step-02:
• Calculate the value of initial decision parameter P0 as-
P0 = 3 – 2 x R
• Suppose the current point is (Xk, Yk) and the next point is (Xk+1,
Yk+1).
• E.g. if current point is (x1, y1) and next point is (x2,y2)
• Find the next point of the first octant depending on the value of
decision parameter Pk.
• There are two cases of decision parameter
• Case 1 – Pk < 0
• Case 2 - Pk >=0

35. Step-04:
• If the given centre point (XC, YC) is not (0, 0), then do the following and plot
the point-
Xplot = Xc + XCU
Yplot = Yc + YCU
• Here, (XcU, YcU) denotes the current value of X and Y coordinates.
Step-05:
• Keep repeating Step-03 and Step-04 until Xplot >= Yplot.
Step-06:
• Step-05 generates all the points for one octant.
• To find the points for other seven octants, follow the eight symmetry property
of circle.

36. Problem-01: Given the centre point coordinates (0, 0)
and radius as 8, generate all the points to form a circle..
Solution-
Given-
Centre Coordinates of Circle (XC, YC) = (0, 0)
Radius of Circle = 10
Step-01:
Assign the starting point coordinates (X0, Y0) as-
X0 = 0
Y0 = R = 8
Step-02:
• Calculate the value of initial decision parameter P0 as-
P0 = 3 – 2 * R
P0 = 3 – 2*8
P0 = -13

37. Step-03:
• As Pinitial < 0, so case-01 is satisfied.
Thus,
Xk+1 = Xk + 1 = 0 + 1 = 1
Yk+1 = Yk = 8
Pk+1 = Pk + 4 x Xk+1 + 6 = -13 + (4 x 1) + 6 = -3
Step-04:
• This step is not applicable here as the given center point
coordinates is (0, 0).
Step-05:
• Step-03 is executed similarly until Xk+1 >= Yk+1 as follows-

38. Pk Pk+1 (Xk+1, Yk+1)
(0, 8)
-13 -3 (1, 8)
-3 11 (2, 8)
11 5 (3, 7)
5 7 (4, 6)
7 (5, 5)
Algorithm Terminates
These are all points for
Octant-1.
ctant-1 Points Octant-2 Points
(0, 8) (5, 5)
(1, 8) (6, 4)
(2, 8) (7, 3)
(3, 7) (8, 2)
(4, 6) (8, 1)
(5, 5) (8, 0)
These are all points for
Quadrant-1. Using Mirror Effect.

39. Quadrant-1 (X,Y) Quadrant-2 (-X,Y) Quadrant-3 (-X,-Y) Quadrant-4 (X,-Y)
(0, 8) (0, 8) (0, -8) (0, -8)
(1, 8) (-1, 8) (-1, -8) (1, -8)
(2, 8) (-2, 8) (-2, -8) (2, -8)
(3, 7) (-3, 7) (-3, -7) (3, -7)
(4, 6) (-4, 6) (-4, -6) (4, -6)
(5, 5) (-5, 5) (-5, -5) (5, -5)
(6, 4) (-6, 4) (-6, -4) (6, -4)
(7, 3) (-7, 3) (-7, -3) (7, -3)
(8, 2) (-8, 2) (-8, -2) (8, -2)
(8, 1) (-8, 1) (-8, -1) (8, -1)
(8, 0) (-8, 0) (-8, 0) (8, 0)
These are all points of the Circle.

40. Transformations
• Translation
• Rotation
• Reflection
• Scaling
• Shear

41. 2D Translation in Computer Graphics
• 2D Translation is a process of moving an object from
one position to another in a two dimensional plane.
𝒙𝒏𝒆𝝎
𝒙𝒐𝒍𝒅
𝒚𝒏𝒆𝝎
𝒚𝒐𝒍𝒅
O
𝑶′
2D Translation

42. • This translation is achieved by adding the translation coordinates to the
old coordinates of the object as-
Xnew = Xold + Tx (This denotes translation towards X axis)
Ynew = Yold + Ty (This denotes translation towards Y axis)

43. Problem-01:
Given a circle C with radius 10 and center coordinates (1, 4). Apply
the translation with distance 5 towards X axis and 1 towards Y axis.
Obtain the new coordinates of C without changing its radius.
• Solution-
Given-
Old center coordinates of C = (Xold, Yold) = (1, 4)
Translation vector = (Tx, Ty) = (5, 1)
Let the new center coordinates of C = (Xnew, Ynew).
Applying the translation equations, we have-
Xnew = Xold + Tx = 1 + 5 = 6
Ynew = Yold + Ty = 4 + 1 = 5
Thus, New center coordinates of C = (6, 5).

44. • In matrix form, the new center coordinates of C
after translation may be obtained as-

45. New center coordinates of C = (6, 5).

46. Problem 2:
Given a square with coordinate points A(0, 3), B(3, 3), C(3, 0), D(0,
0). Apply the translation with distance 1 towards X axis and 1
towards Y axis. Obtain the new coordinates of the square.

47. 2D Rotation
• In Computer graphics, 2D Rotation is a process of
rotating an object with respect to an angle in a two
dimensional plane.
• Consider a point object O has to be rotated from
one angle to another in a 2D plane.
Let-
Initial coordinates of the object O = (Xold, Yold)
Initial angle of the object O with respect to origin = Φ
Rotation angle = θ
New coordinates of the object O after rotation = (Xnew,
Ynew)

49. • This rotation is achieved by using the following
rotation equations-
Xnew = Xold x cosθ – Yold x sinθ
Ynew = Xold x sinθ + Yold x cosθ

50. Problem-01:
Given a line segment with starting point as (0, 0) and ending point as (4, 4). Apply 30 degree
rotation anticlockwise direction on the line segment and find out the new coordinates of the
line.
Given-
Old ending coordinates of the line = (Xold, Yold) = (4, 4)
Rotation angle = θ = 30º
Let new ending coordinates of the line after rotation = (Xnew, Ynew).
Applying the rotation equations, we have-
Xnew
= Xold x cosθ – Yold x sinθ
= 4 x cos30º – 4 x sin30º
= 4 x (√3 / 2) – 4 x (1 / 2)
= 2√3 – 2
= 2(√3 – 1)
= 2(1.73 – 1)
= 1.46

51. Ynew
= Xold x sinθ + Yold x cosθ
= 4 x sin30º + 4 x cos30º
= 4 x (1 / 2) + 4 x (√3 / 2)
= 2 + 2√3
= 2(1 + √3)
= 2(1 + 1.73)
= 5.46
Thus, New ending coordinates of the line after rotation = (1.46,
5.46).

54. Problem
• Triangle ABC having coordinates
• A(2,2)
• B(8,2)
• C(5,5)
• Is to be rotated at angle 90 degree anticlockwise
direction about origin. Find the new position of the
triangle.

55. Reflection
• Reflection is the process of obtaining mirror image of
the original object.
• This is one of the very important transformation as
many engineered products are symmetrical.
• Reflection matrix when multiplied with the original
object coordinates produce mirror of the original
object.
• i.e. P’= PM
• There are some standard cases of reflection which are
as follows

56. Types of Reflection
• Reflection about Y axis
• Reflection about X axis
• Reflection about line Y = X
• Reflection about line Y = -X
• Reflection @ origin
Example: Reflect the triangle ABC having A(1,1),
B(2,1), C(2,3)
Reflection about Y axis