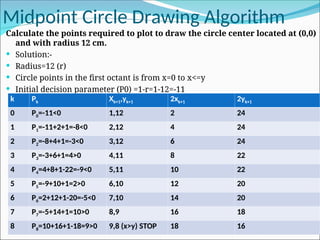
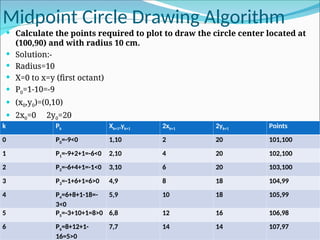
The document outlines various algorithms for drawing lines and circles in computer graphics, focusing on the Digital Differential Analyzer (DDA) and Bresenham's line drawing algorithms. It describes the steps and calculations involved in each algorithm and highlights the advantages of Bresenham's algorithm over DDA due to its improved accuracy in pixel plotting. Additionally, it briefly explains the midpoint circle drawing algorithm and provides mathematical examples for implementing these algorithms.

1. Line, Circle Drawing algorithm
Prepared & Compiled by
Prof. Abhijit Sarkar
IEM, Salt Lake

2. Digital Differential Analyzer Algorithm(DDA)
Cartesian slope-intercept equation for a straight line,
y=mx+b (m=slope, b= y-intercept)
m=dy/dx= y/ x
∆ ∆
b= y1-mx1
Now, case 1:- (|m|<1)
yi=mxi+b
yi+1=m(xi+1)+b
=mxi+m+b
= yi+m
Case 2:- (|m|>1)
xi=(yi-b)/m
xi+1=(yi+1-b)/m
=[(yi-b)/m] + [1/m]
= xi+1/m

3. DDA Algorithm Statement
1) Two endpoints of the line (x1,y1) and (x2,y2) are taken as
input.
2) Slope of the line m=dy/dx= y/ x=(y2-y1)/(x2-x1) is calculated.
∆ ∆
3) First endpoint (x1,y1) is plotted.
4) a. If slope(m)<1, then x-values across the line is increased by
a factor of 1 till x2 is reached and corresponding y-values are
calculated as yi+1= yi+m
4) b. If slope(m)>1, then y-values across the line is increased by
a factor of 1 till y2 is reached and corresponding x-values are
calculated as xi+1= xi+1/m
 Drawback:- DDA algorithm fails to accurately map the
calculated pixel to their nearby screen pixels i.e. scan
conversion is most of the time unsuccessful in this algorithm.
Example:- If calculated position is (11.8) it is mapped to screen
pixel coordinate 11 not 12.

4. Problem on DDA Algorithm
Problem:-
Two endpoints of line are (10,10) and (20,16). Find all
coordinates of pixels over the line using DDA algorithm.
Solution:-
Slope of line(m) = y/ x =16-10/ 20-10=6/10=0.6
∆ ∆
Points are as follows:- [xi+1= xi+1 and yi+1= yi+m]
<10,10>
<11,10+0.6>=<11,10.6>
<12,10.6+0.6>=<12,11.2>
<13,11.2+0.6>=<13,11.8>
<14,11.8+0.6>=<14.12.4>
<15,12.4+0.6>=<15,13>
<16,13+0.6>=<16,13.6>
<17,13.6+0.6>=<17,14.2>
<18,14.2+0.6>=<18,14.8>
<19,14.8+0.6>=<19,15.4>
<20,15.4+0.6>=<20,16>

5. Bresenham’s Line Drawing Algorithm
y=m(xk+1)+b
d1=y-yk = m(xk+1)+b-yk
d2=(yk+1)-y
d1-d2= m(xk+1)+b-yk-yk-1+m(xk+1)+b
= 2m(xk+1)-2yk+2b-1
= 2 y/ x* (x
∆ ∆ k+1)-2yk+2b-1

6. Bresenham’s Line Drawing Algorithm
∆x(d1-d2)= 2 yx
∆ k+2 y -2 xy
∆ ∆ k+2 xb- x
∆ ∆
Now, Pk=2 yx
∆ k-2 xy
∆ k+c where, c=2 y+ x(2b-1) [P
∆ ∆ k= x(d
∆ 1-d2)]
Pk+1=2 yx
∆ k+1-2 xy
∆ k+1+c where, xk+1=xk+1
Pk+1-Pk=2 yx
∆ k+2 y-2 xy
∆ ∆ k+1-2 yx
∆ k+2 xy
∆ k
Pk+1=Pk+2 y-2 x(y
∆ ∆ k+1-yk) Now, yk+1= yk or yk+1
Either 0 or 1
P0=2 yx
∆ k-2 xy
∆ k+c y0=mx0+b= y/ x*x
∆ ∆ 0+b
=2 yx
∆ k-2 xy
∆ k+2 y+ x(2b-1)
∆ ∆ xy
∆ 0= yx
∆ 0+ xb
∆
=2 yx
∆ 0-2 xy
∆ 0+2 y+ x(2b-1)
∆ ∆
=2 yx
∆ 0-2 yx
∆ 0-2 xb+2 y+2 xb- x
∆ ∆ ∆ ∆
= 2 y- x
∆ ∆

7. Bresenham’s Line Drawing Algorithm
1)Two endpoints of the line are taken as input and left
endpoint are stored in (x0,y0).
2)Load (x0,y0) in frame buffer, plot the first point.
3)Calculate P0=2 y- x which is starting value for the
∆ ∆
decision parameter
4)At each xk along the line starting at k=0, if Pk<0 the
next point to plot is (xk+1,yk) and Pk+1=Pk+2 y
∆
Otherwise, the next point to plot is (xk+1,yk+1) and
Pk+1=Pk+2 y-2 x
∆ ∆
5) Repeat step 4 x times.
∆

8. Advantage of Bresenham’s Line
algorithm over DDA algorithm
 The algorithm takes decision of pixel plotting on
the basis of pixel’s calculated(actual) position’s
distance from its upper and lower pixel(which
actually exists on the screen).
 Either upper or lower pixel is selected and
displayed to which the line’s calculated pixel is
closest to.
 Decision parameter checks the above mentioned
criteria and thus removes the DDA algorithm’s
inaccuracy related drawbacks.

9. Mathematical Problem on Bresenham’s
Line algorithm
 Calculate the pixel
positions over the line
having endpoints
(20,10) and (30,18)
using Bresenham’s
line drawing
algorithm.
 ∆x=30-20=10
∆y=18-10=8
Initial decision
parameter P0=2 y-
∆
x=2x8-10=6
∆
X0,y0=20,10
2 y-2 x=16-20=-4
∆ ∆
k Pk xk+1,yk+1
0 6>0 21,11
1 6-4=2>0 22,12
2 2-4=-2<0 23,12
3 -2+16=14>0 24,13
4 14-4=10>0 25,14
5 10-4=6>0 26,15
6 6-4=2>0 27,16
7 2-4=-2<0 28,16
8 -2+16=14>0 29,17
9 14-4=10>0 30,18

10. Mathematical Problem on
Bresenham’s Line algorithm
 Calculate the pixel positions over the line having
endpoints (10,10) and (15,13) using Bresenham’s line
drawing algorithm.
 ∆x=15-10=5
 ∆y=13-10=3
 Initial decision parameter P0=2 y- x=1
∆ ∆
 X0,y0=10,10
 2 y-2 x=6-10=-4
∆ ∆
k Pk xk+1,yk+1
0 1>0 11,11
1 1+6-10=-3<0 12,11
2 -3+6=3>0 13,12
3 3+6-10=-1<0 14,12
4 -1+6=5>0 15,13

11. Midpoint Circle Drawing Algorithm
f circle(x,y)= x2
+y2
-r2
f circle(x,y) <0 means (x,y) is inside circle boundary
=0 means (x,y) is on the circle boundary
>0 means (x,y) is outside circle boundary

12. Midpoint Circle Drawing Algorithm
Assume, (xk,yk) has been plotted.
So, next pixel position will be either (xk+1,yk) or (xk+1,yk-1).
Decision parameter in the circle function evaluated at the midpoint
between these pixels,
Pk=f circle(xk+1,yk-1/2) = (xk+1)2
+(yk-1/2)2
-r2
If Pk<0, midpoint is inside the circle and (xk+1,yk) is taken.
Otherwise, midpoint is outside the circle and (xk+1,yk-1) is taken.

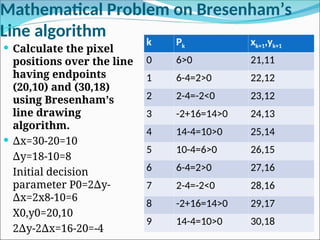
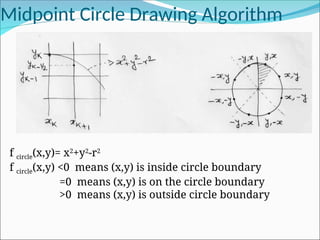
13. Midpoint Circle Drawing Algorithm
 Pk+1=f circle(xk+1+1, yk+1-1/2)
= [(xk+1)+1]2
+ [yk+1-1/2]2
-r2
Pk+1-Pk= (xk+1)2
+1+2(xk+1)+yk+1
2
+1/4-yk+1-r2
-(xk+1)2
-yk
2
-
1/4+yk+r2
= 2(xk+1) + (yk+1
2
-yk
2
)-(yk+1-yk)+1
So, Pk+1=Pk+2(xk+1)+(yk+1
2
-yk
2
)-(yk+1-yk)+1

14. Midpoint Circle Drawing Algorithm
Now,
 Yk+1= yk or yk-1
 If Pk<0 then yk+1=yk
So, Pk+1=Pk+2xk+1+1
 If Pk>0, then yk+1=yk-1
So,
Pk+1=Pk+2xk+1+1+(yk-1)2
–yk
2
-(yk-1-yk)
 = Pk+2xk+1+1+yk
2
+1-2yk-yk
2
+1
 = Pk+2xk+1+1-2yk+2
 = Pk+2xk+1+1-2(yk-1)
 = Pk+2xk+1+1-2yk+1
2xk+1=2(xk+1)=2xk+2
2yk+1=2(yk-1)=2yk-2

15. Midpoint Circle Drawing Algorithm
 Start position=(0,r)
 Initial decision parameter is obtained at start position
(0,r)
 P0=f circle(0+1,r-1/2)
 =(0+1)2
+(r-1/2)2
-r2
 =1+r2
+1/4-r-r2
 =5/4-r
 =1-r (approx.)

16. Midpoint Circle Drawing Algorithm
1. Input radius r and circle center (xc,yc)
2. Obtain the first point on the circumference of a circle
centered on the origin as (x0,y0)=(0,r)
3. Calculate initial value of decision parameter as P0=5/4-
r=1-r
4. At each xk, starting at k=0,
If Pk<0, the next point along the circle centered on (0,0)
is (xk+1,yk) and Pk+1=Pk+2xk+1+1
Else, next point is (xk+1,yk-1) and Pk+1=Pk+2xk+1+1-2yk+1
5. Determine symmetry points in the other 7 octants
6. Move each calculated pixel position (x,y) onto the
circular path centered on (xc,yc)and plot coordinate
values x=x+xc and y=y+yc
7. Repeat step 4 to 6 until x>=y

17. Midpoint Circle Drawing Algorithm
Calculate the points required to plot to draw the circle center located at (0,0)
and with radius 12 cm.
 Solution:-
 Radius=12 (r)
 Circle points in the first octant is from x=0 to x<=y
 Initial decision parameter (P0) =1-r=1-12=-11
k Pk Xk+1,yk+1 2xk+1 2yk+1
0 P0=-11<0 1,12 2 24
1 P1=-11+2+1=-8<0 2,12 4 24
2 P2=-8+4+1=-3<0 3,12 6 24
3 P3=-3+6+1=4>0 4,11 8 22
4 P4=4+8+1-22=-9<0 5,11 10 22
5 P5=-9+10+1=2>0 6,10 12 20
6 P6=2+12+1-20=-5<0 7,10 14 20
7 P7=-5+14+1=10>0 8,9 16 18
8 P8=10+16+1-18=9>0 9,8 (x>y) STOP 18 16

18. Midpoint Circle Drawing Algorithm
 Calculate the points required to plot to draw the circle center located at
(100,90) and with radius 10 cm.
 Solution:-
 Radius=10
 X=0 to x=y (first octant)
 P0=1-10=-9
 (x0,y0)=(0,10)
 2x0=0 2y0=20
k Pk Xk+1,yk+1 2xk+1 2yk+1 Points
0 P0=-9<0 1,10 2 20 101,100
1 P1=-9+2+1=-6<0 2,10 4 20 102,100
2 P2=-6+4+1=-1<0 3,10 6 20 103,100
3 P3=-1+6+1=6>0 4,9 8 18 104,99
4 P4=6+8+1-18=-
3<0
5,9 10 18 105,99
5 P5=-3+10+1=8>0 6,8 12 16 106,98
6 P6=8+12+1-
16=5>0
7,7 14 14 107,97

19. Bresenham’s Circle Drawing Algorithm

20. Parametric equation of Circle
(x,y) be any point on circle at (0,0) origin, t is the angle subtended by
point at the circle’s center. “r” is the radius of circle.
Now, from the diagram,
sin(t)=y/r  y=rsin(t)
cos(t)=x/r  x=rcos(t)
Above two equation forms circle’s parametric equation.
If circle is centered on (h,k) then
x=h+rcos(t) and y=k+rsin(t)
t parameter values are not plotted on an axis.