This document provides a course calendar and lecture plans for topics related to Bayesian estimation methods. The course calendar lists 12 class dates from September to December covering topics like Bayes estimation, Kalman filters, particle filters, hidden Markov models, supervised learning, and clustering algorithms. One lecture plan provides details on the hidden Markov model, including the introduction, definition of HMMs, and problems of evaluation, decoding, and learning. Another lecture plan covers particle filters, including the sequential importance sampling algorithm, choice of proposal density, and the particle filter algorithm of sampling, weight update, resampling, and state estimation.

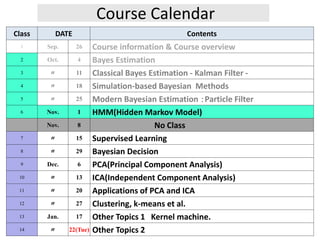
1. Course Calendar
Class DATE Contents
1 Sep. 26 Course information & Course overview
2 Oct. 4 Bayes Estimation
3 〃 11 Classical Bayes Estimation - Kalman Filter -
4 〃 18 Simulation-based Bayesian Methods
5 〃 25 Modern Bayesian Estimation ：Particle Filter
6 Nov. 1 HMM(Hidden Markov Model)
Nov. 8 No Class
7 〃 15 Supervised Learning
8 〃 29 Bayesian Decision
9 Dec. 6 PCA(Principal Component Analysis)
10 〃 13 ICA(Independent Component Analysis)
11 〃 20 Applications of PCA and ICA
12 〃 27 Clustering, k-means et al.
13 Jan. 17 Other Topics 1 Kernel machine.
14 〃 22(Tue) Other Topics 2

2. Lecture Plan
Hidden Markov Model
1. Introduction
2. Hidden Markov Model (HMM)
Discrete-time Markov Chain & HMM
3. Evaluation Problem
4. Decoding Problem
5. Learning Problem

3. 1. Introduction
3
1.1 Discrete-time hidden Markov model (HMM)
The HMM is a stochastic model of a process that can be used for
modeling and estimation. Its distinguishing feature is the probabilistic
model which is driven by internal probability distribution for both
states and measurements. The internal states are usually not observed
directly therefore, are hidden.
1.2 Applications
Discrete representation of stochastic processes:
Speech recognition, Communications, Economics,
Biomedical (DNA analysis), Computer vision (Gesture recognition)

4. 2. HMM
4
2.1 Discrete-time Markov Chains
 
 
  
 
1, 2,
At each time step t, the state variables are defined by
state space
where, .....,
Pr : the probability that at time t the state i is occupied.
1st-order Markovian:
Pr
xN
i
n
x t
x t
x t


X
X X X X
           
    
1 , 2 ,...., 0 Pr 1
Define a :=Pr 1 (time-stationary)
m r l n m
mn n m
x t x t x x t x t
x t x t
   


5.   
 
a set of noisy measurements up to , i.e.,
: 0,1,
, the MAP or Minimum Mean Square Error (MMSE)
estimate of
(Assume the probability densities are represented by continu
t
t
Y y t
x t
  
Given
find
  
ous
PDF such as )tp x t Y
State estimation problem:

6. 1.2 Basic Bayesian Approach (Review)
The state estimation problem in the context of Bayesian approach is
to provide the following relation from Bayes’ rule.
       
       
  
         
          
1
1 1 1 2
1
1 1
2 1 1
,
,
(5)
Likelihood : , (6)
Prediction : 1 1 (7)
Ig
t t
t t
t
t
t t
p x t Y p x t y t Y
p y t x t Y p x t Y N N
Dp y t Y
N p y t x t Y p y t x t
N p x t Y p x t x t p x t Y

 


 

 
  
 
 
   
               1
noring the term
1 1 (8)t t
evicence D
p x t Y p y t x t p x t x t p x t Y   
6
posterior density
at t
posterior density
at t-1
UPDATE

7.     1p x t x t 
  11 tp x t Y 
    p y t x t
  1tp x t Y 
  tp x t Y
t-1
t
Likelihood N1
Prediction PDF N2
posterior PDF at t-1
posterior PDF at t
State transition
Figure Update Scheme

8. 2. Sequential Importance Sampling (SIS)
2.1 Importance Sampling
 
    
      
( ) ( )
( ) ( )
1
N particles: , , ; 1
The posterior approximated by the importance sampling
1
(9)
The weight of the i-th particle at
p
i i i
t p
N
i i
t t t
p i
s state weight x t i N
p x Y x t x t
N
t

 

  
 
  
  
            
 
( )
( )
( )
( ) ( ) ( ) ( )
1( )
( ) (
,
(10)
Using Beyes rule and related equalities, we have a sequential relation as
1 1
i
ti
t i
t
i i i i
ti
t i i
p x t Y
q x t Y
p y t x t p x t x t p x t Y
q x t x




 

     ) ( )
1
(11)
1 , 1i
t tt Y q x t Y  
(SIS-based estimation approach called by particle filter, bootstrap filter, condensation)

9.          
    
( ) ( ) ( )
( )
1( ) ( )
1
(12)
1 ,
i i i
i
ti i
t
p y t x t p x t x t
q x t x t Y
 



     
 
( ) ( )( )
1 1
:
At step , suppose the following approximation by the samples(particles)
1 1 , ; 1 (13)
After observing , we wish to approximate with a new
i ii
t pt
t -1
p x t Y x t i N
y t
   
Problem
    ( )( )
samples at
(14), ; 1 p
jj
t t t
t
p x Y x t j N 
2.2 Choice of the proposal density – Convenient way -
         
    
( ) ( ) ( ) ( )
easy to evaluate
( ) ( )( )
1
1 , 1 (15)
From (12), (16)
i i i i
t
i ii
t t
q x t x t Y p x t x t
p y t x t  
  

update weight
at t
previous weight
at t-1
Likelihood at t

10. 10
3. Particle Filter Algorithm
- Sampling Importance Resampling (SIR) Filter-
(A) Sampling (Prediction)
 
    
(A-1) Generate random values according to
1 1 1, ,
p
i
w P
N
w t p w t i N  
10
 
   
   
  1
(A-2) Compute predicted particles:
1 , 1i i i
tx t f x t w t  
 
  1
,i
pParticles x t N


11. 11
(B) Weight Update
   
  (B-1) Compute the likelihood :
i
p y t x t
 
   
  
(B-2) Update the weight
(19)i i
t p y t x t 
 
 
 
1
(B-3) Normalization
: (20)p
i
i t
t N
j
t
j






 
   
 ,i i
tParticles x t 

12. 12
(C) Resampling for degeneracy avoiding
(C-1) Weighted samples Equal weight samples
 
 
  
ˆThe distribution of gives an approximation of posterior distribution
t
j
x t
p x t Y
         
  1
Now, we have
1
ˆ ˆ
pN
j
t t
jp
p x t Y p x t Y x t x t
N


  
   
 
1
Using above approximation we may obtain an MMSE Estimation as
1
ˆ ˆ
pN
j
jp
x t x t
N 
 
 
   
   
  1
ˆParticles , ,i ji
t px t x t N 

(D) State Estimation
 
   
 ˆ is used for in the next step sampling
(prediction) processes, i.e. go to sampling step A).
ij
x t x t

13. 13
Resampling process in 1-d case:
(C-1) Weighted samples Equal weight samples

14. Revised figure in [ P. M. Djuric et al. Particle Filtering IEEE SP magazine 2003 ]
 t tp y x
 1 1t tp x Y 
 ˆ t tp x Y
t
t+1
Likelihood
Prediction Density
State transition
(A) Sampling
(A) Sampling
 1 1t tp y x 
(C) Resampling
(B) Weight Update
 1
ˆ t tp x Y
Likelihood
(D) State Estimate
(B) Weight Update

15. -Visual tracking object for mobile systems- (moving camera and no static background)
K. Nummiaro et al. “” An adaptive color-based particle filter” Image and Vision
Computing XX (2001) 1-12
Object state model
The state of a particle is modeled as
 
 
 
     
     
     
 
2
: , , , , , ,
, :position of the tracked object by the particle
, : velocity of the tracked object (motion displacement)
:scale change
1
1
1 0,
T
x z x z
x z
x
z
x x Hx
z
x z H H v v a
x z
v v
a
x t x t v t
z t z t v t
H t H t N
H t


  
  
  
Motion model :
x
   2
1 0,z HzH t N   
 ,x z
 ,x zv v
xH
zH
4. Application example of particle filter

16. A distribution p(x) of the state of the object is approximated by
a set of weighted particles,
 
  ( ) ( ) ( )
: , 1
, : importance weight
j
t t
j j j j
t t t
S s j J
s x t  
 

Update process: from one frame to the next frrame
1) motion model
2) new frame gives likelihood of the observation
    ( ) ( )j j
t p y t x t 
    ( )
1j j
p x t x t 
By integrating the J particles the state of the tracked object is
estimated as
   ( ) ( ) ( ) ( ) ( ) ( )
, , , , , , , ,
(weighted average)
TT j j j j j j
x z t x zx z H H a x z H H a 

17.     
 
     
 
 
( )
1
1,....,
Evaluation of the likelihood of the particle, for a new
obsevation :
Color-based similarity measure between color histograms
,
Histogram of target model: ,
Histog
j
m
u u
u
u
u m
p y t x t
y t
p q p q
p p






 
 
 
1,....,
ram of the image of a particle
The distance between two distributions :
: 1 , Bhattacharyya distance
u
u m
q q
d p q


 
2
2( ) 2
Weight of particle based on color distribution likelihood
1
2
d
j
t e 





18. Tracking results by mean shift (left), Kalman+mean shift (middle), Particle filter (right)

19. 19Tracking results for occlusion cases by the color-based Particle filter

20. 20
References：
[1] J. Candy, “ Bayesian Signal Processing Classical, Modern, and Particle Filtering
Methods”, John Wiley/IEEE Press, 2009
[2] B. Ristic, et al. , “Beyond the Kalman Filter”, Artech house Publishers, 2004
[3] F. Asano(浅野太), “Array signal processing for acoustics (音のアレイ信号処理)”,
CORONA publishing Co., LTD, 2011 （Japanese）
[4] M. Isard and A. Blake, “CONDENSATION- Conditioned Density Propagation for
Visual Tracking”, International J. of Computer Vision 29(1), 5-28 (1998)
[5] K. Nummiaro et al. “” An adaptive color-based particle filter”, Image and Vision
Computing XX (2001) 1-12
[6] D. A. Klein et al., Adaptive Real-time video-tracking for arbitrary objects,
Intelligent robotics and …, 2010

21. In practice, it is difficult to generate the samples directly from the
density . Instead, the samples can be generated by , referred
to as importance distribution or proposal distribution, whose PDF is
similar as .
 i
x
 p x  q x
 
   
 
     
 
 
 
Similarity of means:
0 0
In terms of , we have
where : is referred to as the .
q x
p x q x for all x
q x
I f x x q x dx
p x
x importance weght
q x


  



Appendix Importance sampling
- partially revised Section 3.2 in the Lecture 4 slides -
 p x

22.          
The importance sampling approximation of can be written by
N
( i ) ( i )
i
I
ˆ ˆI I f x x q x dx x f x
N
 

    1
1
 
 
 
 
 
     
 
 
 
   ( ) ( )
1
can be evaluated up to a normalization constant, i.e.
( is unknown), q ( is unknown)
Then,
=
1
,
p q
p q
q
p
N
q i i
p i
p x
p x q x
p x Z x Z
Z Z
Z p x
I f x p x dx f x q x dx
Z q x
Z
x f x
Z N


 


 

Case :
 
 
 
( )
( )
( )
i
i
i
p x
x
q x
 

23.  
   
 
( )
( )
1
( )
1
Consider the case ( ), the ratio can be evaluated by using the sample
set as follows.
1
1
1
Thus,
1
i
N
q i
p i
q
N
p i
i
f x
x
Z
p x dx x
Z N
Z
Z
w x
N



 



 
     
 
 
 
( )
( ) ( ) ( )
1 1
( )
( )
( )
1
Therefore,
where :
iN N
i i i
pi i
q
i
i
N
j
j
x
I f x x f x
Z
Z
x
x
x





 

 
 
  
 

 
