KAUST_talk_short.pdf

Automated Importance Sampling via Optimal Control
for Stochastic Reaction Networks:
Learning and Markovian Projection-based Approaches
Chiheb Ben Hammouda
Joint work with
Nadhir Ben Rached (University of Leeds),
Raúl Tempone (RWTH Aachen, KAUST) and
Sophia Wiechert (RWTH Aachen)
Stochastic Numerics and Statistical Learning: Theory and
Applications Workshop
KAUST, May 30, 2023
1

Goal/Main Ideas of the Talk
1 Design of efficient Monte Carlo (MC) estimators for rare event
probabilities for a particular class of continuous-time Markov
chains, namely stochastic reaction networks (SRNs).
2 Automated path dependent measure change is derived based on a
connection between finding optimal importance sampling (IS)
parameters and a stochastic optimal control (SOC) formulation.
3 Address the curse of dimensionality when solving the SOC
problem
(a) Learning-based approach for the value function and controls of
an approximate dynamic programming problem, via stochastic
optimization
C. Ben Hammouda et al. “Learning-based importance sampling via
stochastic optimal control for stochastic reaction networks”. In: Statistics
and Computing 33.3 (2023), p. 58.
(b) Markovian projection-based approach to solve a significantly
reduced-dimensional Hamilton-Jacobi-Bellman (HJB) equations.
C. Ben Hammouda et al. “Automated Importance Sampling via Optimal
Control for Stochastic Reaction Networks: A Markovian Projection-based
Approach”. In: To appear soon (2023). 2

Outline
1 Motivation and Framework
2 Optimal Path dependent Importance Sampling (IS) via Stochastic
Optimal Control (SOC)
Formulation
Learning-based Approach
Markovian Projection (MP)-based Approach
3 Numerical Experiments and Results
Learning-based Approach: Results
MP-based Approach: Results
4 Conclusions
2

1 Motivation and Framework
2 Optimal Path dependent Importance Sampling (IS) via Stochastic
Optimal Control (SOC)
Formulation
Learning-based Approach
Markovian Projection (MP)-based Approach
3 Numerical Experiments and Results
Learning-based Approach: Results
MP-based Approach: Results
4 Conclusions

Stochastic Reaction Networks (SRNs): Motivation
Deterministic models describe an average (macroscopic) behavior
and are only valid for large populations.
Species/Agents of small population ⇒ Dynamics dominated by
stochastic effects.
⇒ Modeling based on Stochastic Reaction Networks (SRNs) using
Poisson processes.
SRNs Applications:
▸ (Bio)chemical reactions/Biological Models (Briat et al. 2015)
▸ Epidemic Processes (Anderson et al. 2015).
▸ Manufacturing supply chain/logistic networks (Chiang et al. 2020).
▸ Social networks/Multi-agent networks/distributed systems
(Goutsias et al. 2013).
▸ Transcription and translation in genomics and virus Kinetics
(Hensel et al. 2009; Roberts et al. 2011).
3

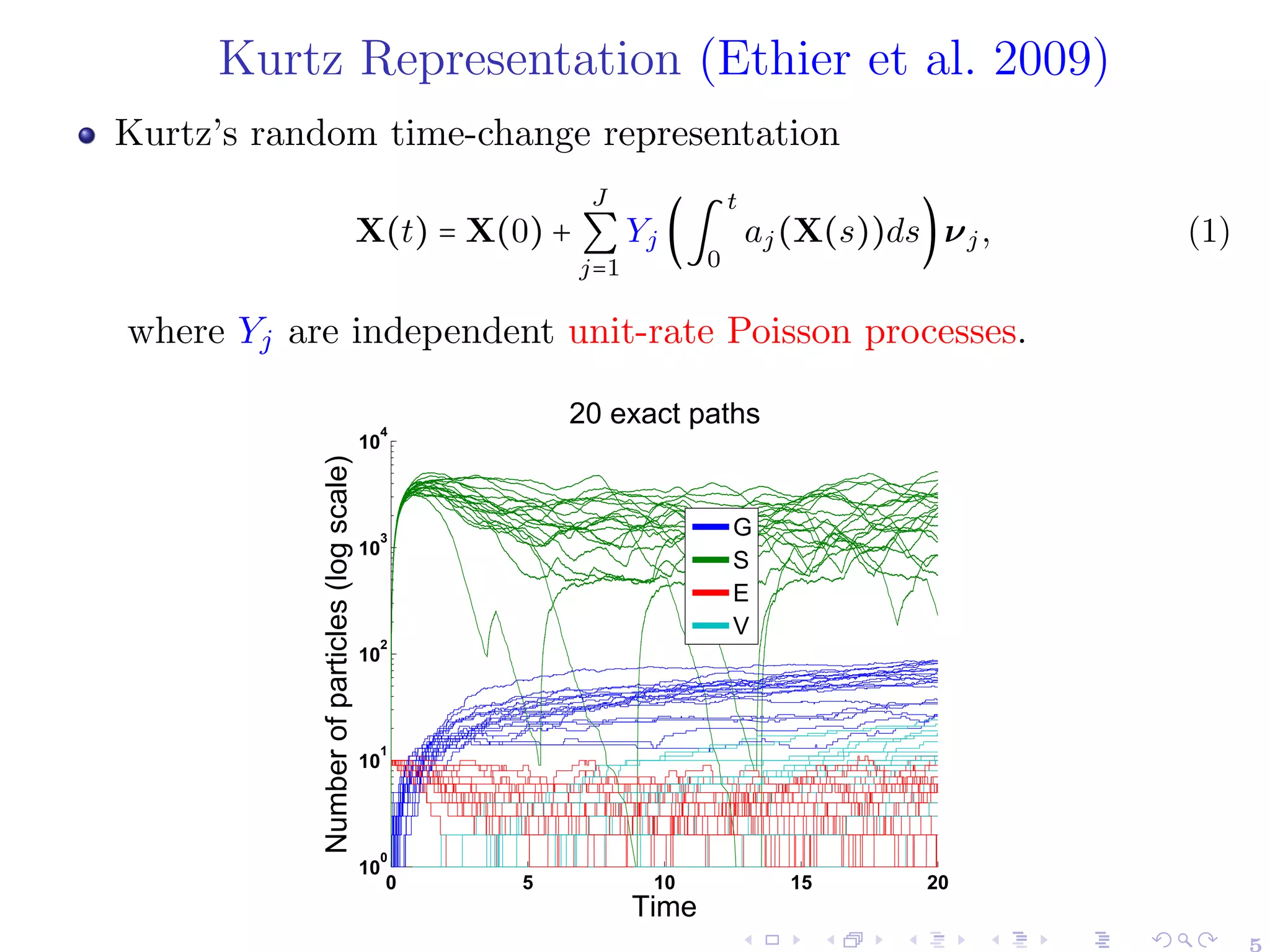
Stochastic Reaction Network (SRNs)
A stochastic reaction network (SRN) is a continuous-time Markov
chain, X(t), defined on a probability space (Ω,F,P)1
X(t) = (X(1)
(t),...,X(d)
(t)) ∶ [0,T] × Ω → Nd
described by J reactions channels, Rj ∶= (νj,aj), where
▸ νj ∈ Zd
: stoichiometric (state change) vector.
▸ aj ∶ Rd
+ → R+: propensity (jump intensity) function.
aj satisfies
P(X(t + ∆t) = x + νj ∣ X(t) = x) = aj(x)∆t + o(∆t), j = 1,...,J.
1
X(i)
(t) may describe the abundance (counting number) of the i-th species
(agent) present in the system at time t. 4

Kurtz Representation (Ethier et al. 2009)
Kurtz’s random time-change representation
X(t) = X(0) +
J
∑
j=1
Yj (∫
t
0
aj(X(s))ds)νj, (1)
where Yj are independent unit-rate Poisson processes.
0 5 10 15 20
10
0
10
1
10
2
10
3
10
4
20 exact paths
Time
Number
of
particles
(log
scale)
G
S
E
V

Simulation of SRNs
Pathwise exact Pathwise approximate
model the exact stochastic distri-
bution of the process
simulation on a time-discrete grid
0 20 40 60 80 100
t
0
50
100
150
200
250
numer
of
molecules
A
B
⊖ computationally expensive ⊖ a bias is introduced (+) faster
● Stochastic Simulation Algo-
rithm (SSA) (Gillespie 1976)
● Explicit Tau-Leap (TL) ap-
proximate scheme (Gillespie
2001)
● Modified Next Reaction
Method (MNRM) (Anderson
2007)
● Split Step Implicit Tau-Leap
(Ben Hammouda et al. 2017)
6

The Explicit-TL Method
(Gillespie 2001; J. Aparicio 2001)
Based on the Kurtz’s random time-change representation (Ethier
et al. 2009)
X(t) = X(0) +
J
∑
j=1
Yj (∫
t
0
aj(X(s))ds)νj,
where Yj are independent unit-rate Poisson processes
The explicit-TL method (forward Euler approximation):
X̂
∆t
0 = x0
X̂
∆t
n = max
⎛
⎝
0,X̂
∆t
n−1 +
J
∑
j=1
Pn,j (aj(X̂
∆t
n−1) ⋅ ∆t)νj
⎞
⎠
for n = 1,...N
▸ X̂
∆t
n is the TL approximation at time tn,
▸ Pn,j(aj(X̂
∆t
n−1) ⋅ ∆t) are conditionally independent Poisson random
variables with rate aj(X̂
∆t
n−1)∆t.
▸ 0 = t0 < t1 < ⋅⋅⋅ < tN = T be a uniform grid with step size ∆t

Importance Sampling (IS) for MC
Let Y be a real r.v.
IS is a change of measure, and it reduces the MC computational
cost by sampling on regions with the most effect on the QoI.
Instead of approximating EP
[Y ] with MC, IS uses MC for
EQ
[Y dP
dQ ].
The minimum variance is then
V arQ∗
[Y
dP
dQ∗
] = (EP
[∣Y ∣])
2
(1 − (EQ∗
[1{Y >0}] − EQ∗
[1{Y <0}])
2
)
IS-MC will be more efficient than plain MC when
V arP
[Y ]/(EP
[∣Y ∣])
2
>> 1 or Y has near constant sign, i.e.
V arQ∗
[Y
dP
dQ∗
](1 + θ) < V arP
[Y ]
Here (1 + θ) ≥ 1 is the relative cost of sampling Y dP
dQ∗ under Q∗
wrt sampling Y under P.
8

Aim and Setting
Design a computationally efficient MC estimator for
E[g(X(T))] using IS:
▸ We are interested in g(X(T)) = 1{X(T )∈B} for a set B ⊆ Nd
for
rare event applications: E[g(X(T))] = P(X(T) ∈ B) ≪ 1
▸ {X(t) ∶ t ∈ [0,T]} is a SRNs.
Challenge
IS often requires insights into the given problem.
Solution
Propose an automated path dependent measure change based on a
novel connection between finding optimal IS parameters and a SOC
formulation, corresponding to solving a variance minimization
problem.

Introduction of the IS Scheme
Recall the TL approximate scheme for SRNs with step size ∆t:
X̂
∆t
n+1 = max
⎛
⎝
0,X̂
∆t
n +
J
∑
j=1
νjPn,j (aj(X̂
∆t
n )∆t)
⎞
⎠
, n = 0,...,N − 1
We introduce the following change of measure:2
Pn,j = Pn,j(δ∆t
n,j(X
∆t
n )∆t), n = 0,...,N − 1,j = 1,...,J,
where δ∆t
n,j(x) ∈ Ax,j is the control parameter at time step n,
under reaction j and in state x ∈ Nd
for an admissible set of
Ax,j =
⎧
⎪
⎪
⎨
⎪
⎪
⎩
{0} ,if aj(x) = 0
{y ∈ R ∶ y > 0} ,otherwise
.
2
A similar class of measure change was previously introduced in (Ben Hammouda
et al. 2020) to improve the MLMC estimator robustness and performance.

SOC Formulation for the IS scheme
Aim: Find IS parameters which result in the lowest possible variance
Value Function
Let u∆t(⋅,⋅) be the value function which gives the optimal second
moment. For time step 0 ≤ n ≤ N and state x ∈ Nd
:
u∆t(n,x) ∶= inf
{δ∆t
i }i=n,...,N−1∈AN−n
E[g2
(X
∆t
N )
N−1
∏
i=n
Li(P i,δ∆t
i (X
∆t
i ))
´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶
likelihood factor
2
∣X
∆t
n = x]
Notation:
A = ⨉x∈Nd ⨉J
j=1 Ax,j is the admissible set for the IS parameters.
Li(P i,δ∆t
i (X
∆t
i )) =
exp(−(∑J
j=1 aj(X
∆t
i ) − δ∆t
i,j (X
∆t
i ))∆t) ⋅ ∏J
j=1 (
aj(X
∆t
i )
δ∆t
i,j (X
∆t
i )
)
Pi,j
(P i)j ∶= Pi,j and (δi)j ∶= δi,j
" Compared with the classical SOC formulation, our expected total
cost uses a multiplicative cost structure rather than the additive one.
11

Dynamic Programming (DP) for IS Parameters
Theorem ((Ben Hammouda et al. 2023b))
For x ∈ Nd
and given step size ∆t > 0, the value function u∆t(⋅,⋅) fulfills
the following dynamic programming relation for n = N − 1,...,0
u∆t(n,x) = inf
δ∆t
n (x)∈Ax
exp
⎛
⎝
⎛
⎝
−2
J
∑
j=1
aj(x) +
J
∑
j=1
δ∆t
n,j(x)
⎞
⎠
∆t
⎞
⎠
× ∑
p∈NJ
J
∏
j=1
(∆t ⋅ δ∆t
n,j(x))pj
pj!
(
aj(x)
δ∆t
n,j(x)
)2pj
⋅ u∆t(n + 1,max(0,x + νp))
for x ∈ Nd
, Ax ∶= ⨉J
j=1 Ax,j and final condition u∆t(N,x) = g2
(x).
" Solving the minimization problem analytically is difficult due to the
infinite sum.
Notation:
ν = (ν1,...,νJ ) ∈ Zd×J
.
12

Approximate DP and near-Optimal IS Parameters
Idea: Approximate the value function u∆t(n,x) by Taylor expansion, and
truncation of the Taylor series and the infinite sum up to O(∆t2
)
u∆t(N,x) = g2
(x) , and for x ∈ N and n = N − 1,...,0 ∶
u∆t(n,x) = u∆t(n + 1,x)
⎛
⎝
1 − 2∆t
J
∑
j=1
aj(x)
⎞
⎠
+ ∆t ⋅
J
∑
j=1
Q∆t
(n,j,x).
For u∆t(n + 1,max(0,x + νj)) ≠ 0 (1 ≤ j ≤ J) and u∆t(n + 1,x) ≠ 0 :
δ
∆t
n,j(x) =
aj(x)
√
u∆t(n + 1,max(0,x + νj))
√
u∆t(n + 1,x)
Q∆t
(n,j,x) ∶= inf
δj ∈Ax,j
[
a2
j (x)
δj
u∆t(n + 1,max(0,x + νj)) + δju∆t(n + 1,x)]
= 2aj(x)
√
u∆t(n + 1,max(0,x + νj)) ⋅ u∆t(n + 1,x)
" Our numerical approximation reduces the complexity of the original
problem at each step from a simultaneous optimization over J variables to
decoupled/independent one-dimensional ones that can be solved in parallel.
" The conditions for attainability ensured either by some regularization
(Wiechert 2021) or modeling u∆t(⋅,⋅) using a strictly positive ansatz
function as in (Ben Hammouda et al. 2023b). 13

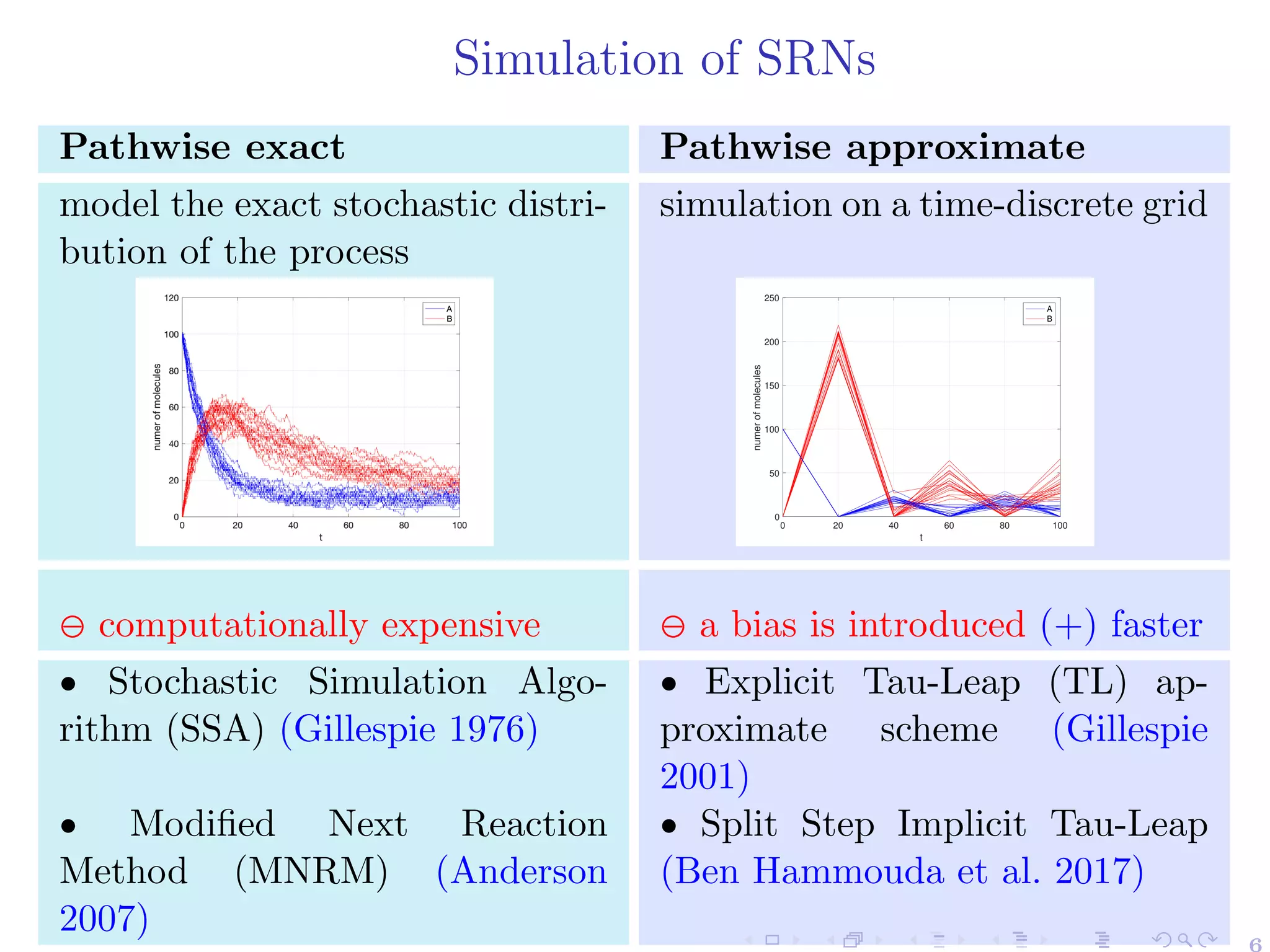
Numerical Dynamic Programming:
Curse of Dimensionality
The computational cost to numerically solve the previous dynamic
programming equation for step size ∆t and truncated state space
⨉d
i=1[0,Si] ⊂ Nd
can be expressed as
W(S,∆t) ≈
T
∆t
⋅ J ⋅ (S
∗
)d
, S̄∗
= max
i=1,...,d
S̄i
⊖ Computational cost scales exponentially with dimension d.

Our Approaches to Address the Curse of Dimensionality
Optimal IS (control) parameters:
δ
∆t
n,j(x) =
aj(x)
√
u∆t(n + 1,max(0,x + νj))
√
u∆t(n + 1,x)
(2)
Markovian projection-based
approach (Ben Hammouda
et al. 2023a):
● Numerical approximation of
u∆t(n,x) via solving a
significantly lower dimensional
HJB
Learning-based approach
(Ben Hammouda et al.
2023b):
● Model u∆t(n,x) by a
parametrized ansatz function
û∆t(n,x;β)
● β learned by stochastic
optimization
Suitable when the
projected dimension is very
low (potentially even one)
Suitable when a
relevant ansatz exists

Learning-based Approach: Illustration
full-
dimensional
SRN
X(t) ∈ Rd
Paramterized
Ansatz
for Value
Function
Parameter Learning for Value Function
IS forward run
to derive gradient
IS forward
run using (2)
Efficient MC-IS estimator
IS Sample Paths for training
Parameter Update via
stochastic optimization
16

Learning-based Approach: Steps
1 Approximate the value function, u∆t(n,x), with an ansatz function, û(t,x;β):
u∆t(n,x) = inf
{δ∆t
i }i=n,...,N−1∈AN−n
E[g2
(X
∆t
N )
N−1
∏
i=n
Li(P̄ i,δ∆t
i (X
∆t
i ))
´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶
likelihood factor
2
∣X
∆t
n = x].
Illustration: For the observable g(X(T)) = 1{Xi(T)>γ} , we use the ansatz
û(t,x;β) =
1
1 + e−(1−t)⋅(<βspace
,x>+βtime)+b0−<β0,x>
, t ∈ [0,1], x ∈ Nd
learned parameters β = (βspace
,βtime
) ∈ Rd+1
, and
b0 and β0 are chosen to fit the final condition at time T (not learned)
Example sigmoid for d = 1:
● final fit for g(x) = 1{xi>10}
→ b0 = 14,β0 = 1.33
● βspace
= −0.5, βtime
= 1
17

Learning-Based Approach: Steps
2 Use stochastic optimization (e.g. ADAM (Kingma et al. 2014))
to learn the parameters β = (βspace
,βtime
) ∈ Rd+1
which minimize
the second moment under IS:
inf
β∈Rd+1
E[g2
(X
∆t,β
N )
N−1
∏
k=0
L2
k (P̄ k,δ̂
∆t
(k,X
∆t,β
k ;β))]
´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶
=∶C0,X (δ̂
∆t
0 ,...,δ̂
∆t
N−1;β)
,
▸ (δ̂
∆t
(n,x;β))
j
= δ̂∆t
j (n,x;β) =
aj (x)
√
û∆t(
(n+1)∆t
T ,max(0,x+νj );β)
√
û∆t(
(n+1)∆t
T ,x;β)
▸ {X
∆t,β
n }n=1,...,N is an IS path generated with {δ̂
∆t
(n,x;β)}n=1,...,N
(+) We derive explicit pathwise derivatives, which are unbiased,
resulting in only the MC error for evaluating the expectation (i.e.,
without additional finite difference error).
18

Partial Derivatives of the Second Moment
Lemma ((Ben Hammouda et al. 2023b))
The partial derivatives of the second moment C0,X (δ̂
∆t
0 ,...,δ̂
∆t
N−1;β)
with respect to βl, l = 1,...,(d + 1), are given by
∂
∂βl
E
⎡
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
g2
(X
∆t,β
N )
N−1
∏
k=0
L2
k (P̄ k,δ̂
∆t
(k,X
∆t,β
k ;β))
´¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¸¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¹¶
=∶R(X0;β)
⎤
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
= E
⎡
⎢
⎢
⎢
⎢
⎢
⎣
R(X0;β)
⎛
⎜
⎝
N−1
∑
k=1
J
∑
j=1
⎛
⎜
⎝
∆t −
P̄k,j
δ̂∆t
j (k,X
∆t,β
k ;β)
⎞
⎟
⎠
⋅
∂
∂βl
δ̂∆t
j (k,X
∆t,β
k ;β)
⎞
⎟
⎠
⎤
⎥
⎥
⎥
⎥
⎥
⎦
,
where
{X
∆t,β
n }n=1,...,N is an IS path generated with {δ̂
∆t
(n,x;β)}n=1,...,N
∂
∂βl
δ̂∆t
j (k,X;β) is found in a closed form

Learning-Based Approach: Steps
3 In the forward step, estimate E[g(X(T))] using the MC estimator
based on the proposed IS change of measure over M paths
µIS
M,∆t =
1
M
M
∑
i=1
Lβ∗
i ⋅ g(X
∆t,β∗
[i],N ),
where X
∆t,β∗
[i],N is the i-th IS sample path and Lβ∗
i is the
corresponding likelihood factor, both simulated with the IS
parameters obtained via the stochastic optimization step
δ̂j(n,x;β∗
) =
aj(x)
√
û((n+1)∆t
T
,max(0,x + νj);β∗
)
√
û((n+1)∆t
T
,x;β∗
)
, 0 ≤ n ≤ N − 1, x ∈ Nd
,
,1 ≤ j ≤ J
20

HJB equations for IS Parameters
of the full-dimensional SRNs
Corollary (Ben Hammouda et al. 2023a)
For x ∈ Nd
, an approximate continuous-time value function ũ(t,x) fulfills the
Hamilton-Jacobi-Bellman (HJB) equations for t ∈ [0,T]
ũ(T,x) = g2
(x)
−
dũ
dt
(t,x) = inf
δ(t,x)∈Ax
⎛
⎝
−2
J
∑
j=1
aj(x) +
J
∑
j=1
δj(t,x)
⎞
⎠
ũ(t,x) +
J
∑
j=1
aj(x)2
δj(t,x)
ũ(t,max(0,x + νj)),
where δj(t,x) ∶= (δ(t,x))j.
For If ũ(t,x) > 0 for all x ∈ Nd
and t ∈ [0,T] :
▸ δ̃j(t,x) = aj(x)
√
ũ(t,max(0,x+νj ))
ũ(t,x)
▸ dũ
dt
(t,x) = −2∑
J
j=1 aj(x)(
√
ũ(t,x)ũ(t,max(0,x + νj)) − ũ(t,x))
For rare event probabilities, we approximate the observable g(x) = 1xi>γ
by a sigmoid: g̃(x) = 1
1+exp(b−βxi), with appropriately chosen parameters
b ∈ R and β ∈ R.
⊖ Computational cost to solve HJB Equ. scales exponentially with dimension
d.

MP-based Approach: Illustration
full-
dimensional
SRN
X(t) ∈ Rd
projected SRN
S̄(t) ∈ R¯
d, d̄ ≪ d
Markovian
Projection
solving (reduced
dimensional)
d̄-dim HJB equ.
projected
IS controls
IS forward run
for (full-dimensional)
d-dim SRN
Efficient MC-IS estimator
22

Markovian Projection (MP): Idea
Recall: A SRN X(t) is characterized by (Ethier et al. 2009)
X(t) = x0 +
J
∑
j=1
Yj (∫
t
0
aj(X(s))ds)νj, (3)
where Yj ∶ R+×Ω → N are independent unit-rate Poisson processes.
Let P be a projection to a ¯
d-dimensional space (1 ≤ ¯
d ≪ d),
P ∶ Rd
→ R
¯
d
∶ x ↦ P ⋅ x,
While X is Markovian, S(t) ∶= P ⋅ X(t) is non-Markovian.
We want to adapt the MP idea, originally introduced in (Gyöngy
1986) for the setting of diffusion type SDEs, to the SRNs
framework, where we construct a low dimensional Markovian
process that mimics the evolution of S.
The choice of the projection depends on the QoI, e.g., for
observable g(x) = 1{xi>γ}, a suitable projection is
P(x) = ⟨(0, . . . , 0
i−1
, 1
i
, 0
i+1
, . . . , 0)⊺
, x⟩ .
23

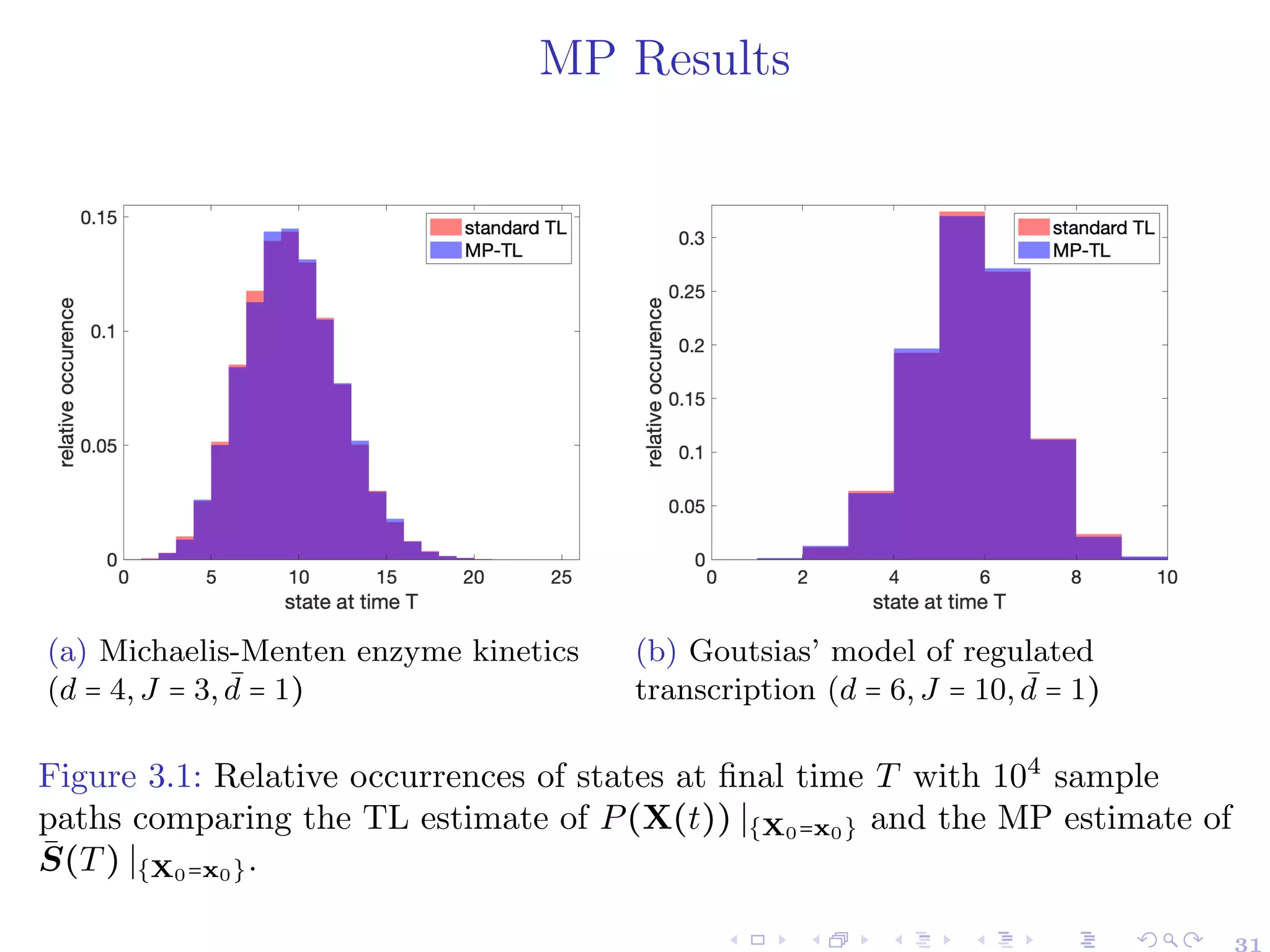
Markovian Projection for SRNs
For t ∈ [0,T], let us consider the projected process as S(t) ∶= P ⋅ X(t),
where X(t) follows (3).
Theorem ((Ben Hammouda et al. 2023a))
For t ∈ [0,T], let S̄(t) be a ¯
d-dimensional stochastic process, whose
dynamics are given by
S̄(t) = P(x0) +
J
∑
j=1
Ȳj (∫
t
0
āj(τ,S̄(τ))dτ)P(νj)
´¹¹¹¹¹¹¸¹¹¹¹¹¹¶
=∶ν̄j
,
where Ȳj are independent unit-rate Poisson processes and āj are
characterized by
āj(t,s) ∶= E[aj(X(t))∣P (X(t)) = s,X(0) = x0], for 1 ≤ j ≤ J,s ∈ N
¯
d
.
Then, S(t) ∣{X(0)=x0} and S̄(t) ∣{X(0)=x0} have the same conditional
distribution for all t ∈ [0,T].
24

Propensities of the Projected Process
Under MP, the propensity becomes time-dependent
āj(t,s) ∶= E[aj(X(t)) ∣ P (X(t)) = s;X(0) = x0], for 1 ≤ j ≤ J,s ∈ N
¯
d
The index set of the projected propensities is (#JMP ≤ J)
JMP ∶= {1 ≤ j ≤ J ∶ P(νj) ≠ 0 and aj(x) ≠ f(P(x)) ∀f ∶ R
¯
d
→ R}.
To approximate āj for j ∈ JMP , we use discrete L2
regression:
āj(⋅,⋅) = argminh∈V ∫
T
0
E[(aj(X(t)) − h(t,P(X(t))))
2
]dt
≈ argminh∈V
1
M
M
∑
m=1
1
N
N−1
∑
n=0
(aj(X̂∆t
[m],n) − h(tn,P(X̂∆t
[m],n)))
2
▸ V ∶= {f ∶ [0,T] × R
¯
d
→ R ∶ ∫
T
0 E[f(t,P(X(t))2
)]dt < ∞}
▸ {X̂∆t
[m]}
M
m=1
are M independent TL paths on a uniform time grid
0 = t0 < t1 < ⋅⋅⋅ < tN = T with step size ∆t.
25

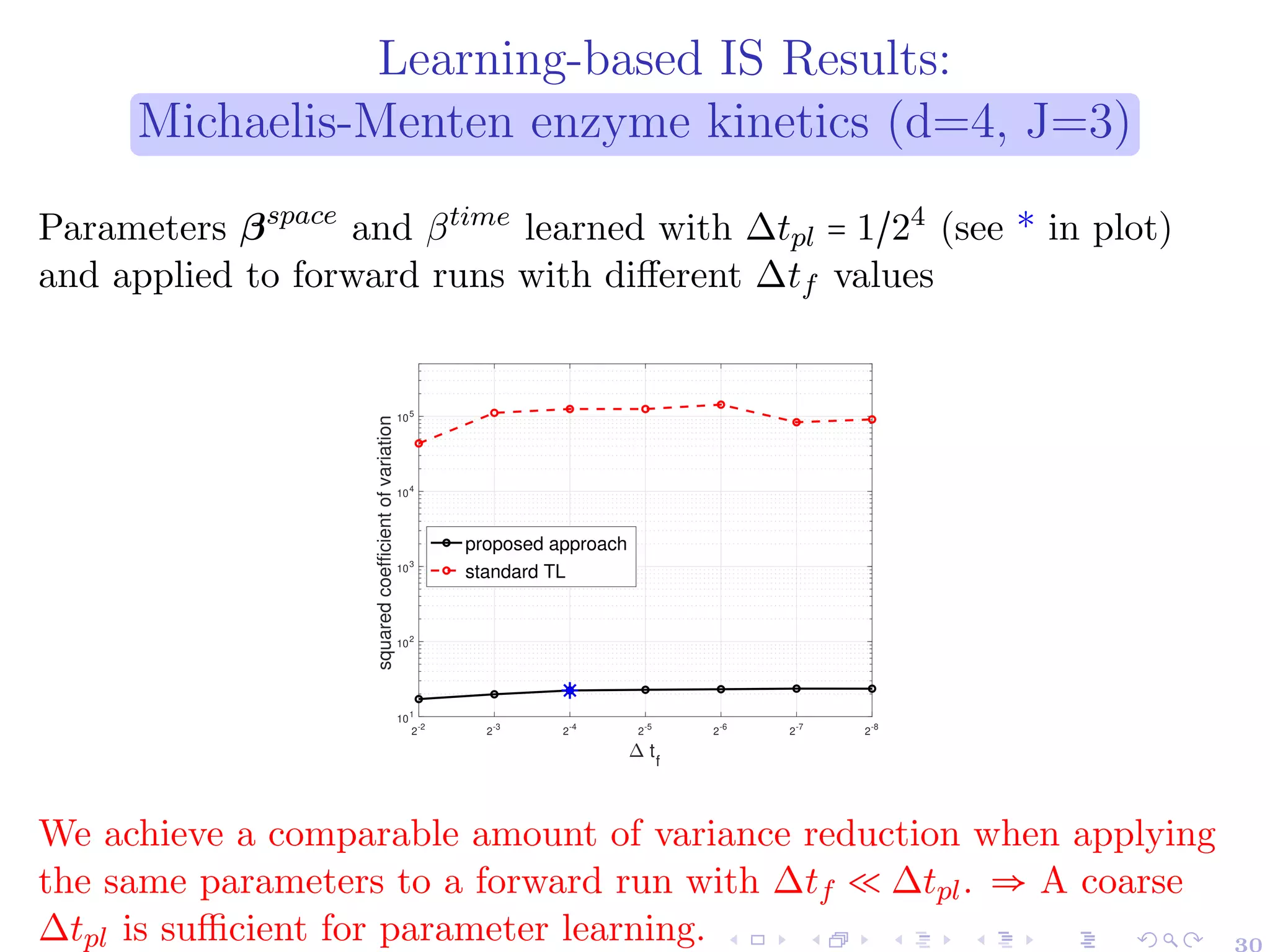
IS for SRNs via MP: Steps
1 Perform the MP as described in the previous slides
2 For t ∈ [0,T], solve the reduced-dimensional HJB equations
(system of ODEs) corresponding to the MP process
ũ¯
d(T,s) = g̃2
(s), s ∈ N
¯
d
dũ¯
d
dt
(t,s) = −2
J
∑
j=1
āj(t,s)(
√
ũ¯
d(t,s)ũ¯
d(t,max(0,s + ν̄j)) − ũ¯
d(t,s)), s ∈ N
¯
d
.
3 Obtain the continuous-time IS controls for the d-dimensional SRN
δ̄j(t,x) = aj(x)
¿
Á
Á
Àũ¯
d (t,max(0,P(x + νj)))
ũ¯
d (t,P(x))
, for x ∈ Nd
,t ∈ [0,T].
4 Construct the MP-IS-MC estimator for a given uniform time grid
0 = t0 ≤ t1 ≤ ⋅⋅⋅ ≤ tN = T with stepsize ∆t, with TL paths using the
IS control parameters δ̄j(tn,x), j = 1,...,J,x ∈ Nd
,n = 0,...,N − 1.
26

Examples
Michaelis-Menten enzyme kinetics (d=4, J=3) (Rao et al. 2003)
E + S
θ1
→ C, C
θ2
→ E + S, C
θ3
→ E + P,
▸ initial states X0 = (E(0),S(0),C(0),P(0))⊺
= (100,100,0,0)⊺
,
▸ θ = (0.001,0.005,0.01)⊺
,
▸ final time T = 1, and
▸ observable g(X(T)) = 1{X3(T )>22} → P(X3(T) > 22) ≈ 10−5
Enzymatic futile cycle model (d=6, J=6) (Kuwahara et al. 2008)
R1 ∶ S1 + S2
θ1
Ð→ S3, R2 ∶ S3
θ2
Ð→ S1 + S2, R3 ∶ S3
θ3
Ð→ S1 + S5,
R4 ∶ S4 + S5
θ4
Ð→ S6, R5 ∶ S6
θ5
Ð→ S4 + S5, R6 ∶ S6
θ6
Ð→ S4 + S2.
▸ initial states (S1(0),...,S6(0)) = (1,50,0,1,50,0)
▸ θ1 = θ2 = θ4 = θ5 = 1, and θ3 = θ6 = 0.1,
▸ final time T = 2, and
▸ observable g(X(T)) = 1{X5(T )>60} → P(X5(T) > 60) ≈ 10−6
Goutsias’s model of regulated transcription (d=6, J=10)
(Goutsias 2005; Kang et al. 2013):
observable g(X(T)) = 1{X2(T)>8} → P(X2(T) > 8) ≈ 10−3
27

Learning-based Results:
Michaelis-Menten enzyme kinetics (d=4, J=3)
g(X(T)) = 1{X3(T)>22} → P(X3(T) > 22) ≈ 10−5
(∆t = 1/24
)
0 5 10 15 20 25 30 35 40 45 50
Optimizer steps
0.5
1
1.5
2
mean
10
-5
proposed approach
standard TL
0 5 10 15 20 25 30 35 40 45 50
Optimizer steps
10
1
10
2
10
3
10
4
105
squared
coefficient
of
variation
proposed approach
standard TL
0 5 10 15 20 25 30 35 40 45 50
Optimizer steps
-0.3
-0.2
-0.1
0
0.1
0.2
0.3
Parameter
value
space
1
space
2
space
3
space
4
time
0 5 10 15 20 25 30 35 40 45 50
Optimizer steps
10
2
10
3
10
4
105
kurtosis
proposed approach
standard TL
Variance reduction of a factor 4 × 103
after few iterations (∼ 5 iterations).
28

Learning-based IS Results:
Enzymatic futile cycle (d=6, J=6)
g(X(T)) = 1{X5(T)>60} → P(X5(T) > 60) ≈ 10−6
(∆t = 1/24
)
0 10 20 30 40 50 60 70 80 90 100
Optimizer steps
10
-8
10
-7
10
-6
10
-5
10-4
10-3
mean
proposed approach
standard TL
0 10 20 30 40 50 60 70 80 90 100
Optimizer steps
104
10
5
squared
coefficient
of
variation
proposed approach
standard TL
0 10 20 30 40 50 60 70 80 90 100
Optimizer steps
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
Parameter
value
space
1
space
2
space
3
space
4
space
5
space
6
time
0 10 20 30 40 50 60 70 80 90 100
Optimizer steps
10
4
10
5
kurtosis
proposed approach
standard TL
Variance reduction of a factor 50 after 43 iterations.
29

Learning-based IS Results:
Michaelis-Menten enzyme kinetics (d=4, J=3)
Parameters βspace
and βtime
learned with ∆tpl = 1/24
(see * in plot)
and applied to forward runs with different ∆tf values
2
-2
2
-3
2
-4
2
-5
2
-6
2
-7
2
-8
tf
10
1
10
2
10
3
10
4
105
squared
coefficient
of
variation
proposed approach
standard TL
We achieve a comparable amount of variance reduction when applying
the same parameters to a forward run with ∆tf ≪ ∆tpl. ⇒ A coarse
∆tpl is sufficient for parameter learning. 30

MP Results
(a) Michaelis-Menten enzyme kinetics
(d = 4, J = 3, ¯
d = 1)
(b) Goutsias’ model of regulated
transcription (d = 6, J = 10, ¯
d = 1)
Figure 3.1: Relative occurrences of states at final time T with 104
sample
paths comparing the TL estimate of P(X(t)) ∣{X0=x0} and the MP estimate of
S̄(T) ∣{X0=x0}.
31

MP-IS Results:
Michaelis-Menten enzyme kinetics (d = 4,J = 3, ¯
d = 1)
g(X(T)) = 1{X3(T)>22} → P(X3(T) > 22) ≈ 10−5
2-2
2-3
2-4
2-5
2-6
2-7
2-8
2-9
2-10
2-11
2-12
t
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
2.2
sample
mean
10
-5
MP-IS
standard TL
2-2
2-3
2-4
2-5
2-6
2-7
2-8
2-9
2-10
2-11
2-12
t
10-1
10
0
101
10
2
103
104
10
5
10
6
squared
coefficient
of
variation
MP-IS
standard TL
Variance reduction of a factor 106
for ∆t = 2−10
.
32

MP-IS Results:
Goutsias’ model (d=6, J=10, ¯
d = 1)
g(X(T)) = 1{X2(T)>8} → P(X2(T) > 8) ≈ 10−3
2-2
2-3
2-4
2-5
2-6
2-7
2-8
2-9
2-10
t
1
2
3
4
5
6
7
sample
mean
10
-3
MP-IS
standard TL
2-2
2-3
2-4
2-5
2-6
2-7
2-8
2-9
2-10
t
100
101
102
10
3
squared
coefficient
of
variation
MP-IS
standard TL
Variance reduction of a factor 500 for ∆t = 2−10
.
33

Remark: Adaptive MP
There could exist examples, where a projection to dimension ¯
d = 1
is not sufficient to achieve a desired variance reduction.
In this case, one can adaptively increase the dimension of
projection ¯
d = 1,2,... until a sufficient variance reduction is
achieved.
This comes with an increased computational cost in the MP and
in solving the projected HJB equations.
34

Conclusion and Contributions
1 Design of efficient Monte Carlo (MC) estimators for rare event
probabilities for a particular class of continuous-time Markov
chains, namely stochastic reaction networks (SRNs).
2 Automated path dependent measure change is derived based on a
connection between finding optimal importance sampling (IS)
parameters and a stochastic optimal control (SOC) formulation.
3 Address the curse of dimensionality when solving the SOC
problem
(a) Learning-based approach for the value function and controls of
an approximate dynamic programming problem, via stochastic
optimization
(b) Markovian projection-based approach to solve a significantly
reduced-dimensional Hamilton-Jacobi-Bellman (HJB) equation.
4 Our analysis and numerical experiments in (Ben Hammouda et al.
2023a; Ben Hammouda et al. 2023b) show that the proposed
approaches substantially reduces MC estimator variance, resulting
in a lower computational complexity in the rare event regime than
standard MC estimators. 35

Related References
Thank you for your attention!
[1] C. Ben Hammouda, N. Ben Rached, R. Tempone, S. Wiechert. Automated
Importance Sampling via Optimal Control for Stochastic Reaction
Networks: A Markovian Projection-based Approach. To appear soon (2023).
[2] C. Ben Hammouda, N. Ben Rached, R. Tempone, S. Wiechert.
Learning-based importance sampling via stochastic optimal control for
stochastic reaction networks. Statistics and Computing, 33, no. 3 (2023).
[3] C. Ben Hammouda, N. Ben Rached, R. Tempone. Importance sampling for
a robust and efficient multilevel Monte Carlo estimator for stochastic
reaction networks. Statistics and Computing, 30, no. 6 (2020).
[4] C. Ben Hammouda, A. Moraes, R. Tempone. Multilevel hybrid split-step
implicit tau-leap. Numerical Algorithms, 74, no. 2 (2017).
36

References I
[1] David F Anderson. “A modified next reaction method for simulating chemical
systems with time dependent propensities and delays”. In: The Journal of chemical
physics 127.21 (2007), p. 214107.
[2] David F Anderson and Thomas G Kurtz. Stochastic analysis of biochemical systems.
Springer, 2015.
[3] C. Ben Hammouda et al. “Automated Importance Sampling via Optimal Control for
Stochastic Reaction Networks: A Markovian Projection-based Approach”. In: To
appear soon (2023).
[4] C. Ben Hammouda et al. “Learning-based importance sampling via stochastic
optimal control for stochastic reaction networks”. In: Statistics and Computing 33.3
(2023), p. 58.
[5] Chiheb Ben Hammouda, Alvaro Moraes, and Raúl Tempone. “Multilevel hybrid
split-step implicit tau-leap”. In: Numerical Algorithms 74.2 (2017), pp. 527–560.
[6] Chiheb Ben Hammouda, Nadhir Ben Rached, and Raúl Tempone. “Importance
sampling for a robust and efficient multilevel Monte Carlo estimator for stochastic
reaction networks”. In: Statistics and Computing 30.6 (2020), pp. 1665–1689.
[7] Corentin Briat, Ankit Gupta, and Mustafa Khammash. “A Control Theory for
Stochastic Biomolecular Regulation”. In: SIAM Conference on Control Theory and
its Applications. SIAM. 2015.
37

References II
[8] Nai-Yuan Chiang, Yiqing Lin, and Quan Long. “Efficient propagation of
uncertainties in manufacturing supply chains: Time buckets, L-leap, and multilevel
Monte Carlo methods”. In: Operations Research Perspectives 7 (2020), p. 100144.
[9] Stewart N Ethier and Thomas G Kurtz. Markov processes: characterization and
convergence. Vol. 282. John Wiley & Sons, 2009.
[10] D. T. Gillespie. “Approximate accelerated stochastic simulation of chemically
reacting systems”. In: Journal of Chemical Physics 115 (July 2001), pp. 1716–1733.
doi: 10.1063/1.1378322.
[11] Daniel Gillespie. “Approximate accelerated stochastic simulation of chemically
reacting systems”. In: The Journal of chemical physics 115.4 (2001), pp. 1716–1733.
[12] Daniel T Gillespie. “A general method for numerically simulating the stochastic time
evolution of coupled chemical reactions”. In: Journal of computational physics 22.4
(1976), pp. 403–434.
[13] John Goutsias. “Quasiequilibrium approximation of fast reaction kinetics in
stochastic biochemical systems”. In: The Journal of chemical physics 122.18 (2005),
p. 184102.
[14] John Goutsias and Garrett Jenkinson. “Markovian dynamics on complex reaction
networks”. In: Physics reports 529.2 (2013), pp. 199–264.
38

References III
[15] István Gyöngy. “Mimicking the one-dimensional marginal distributions of processes
having an Itô differential”. In: Probability theory and related fields 71.4 (1986),
pp. 501–516.
[16] SebastianC. Hensel, JamesB. Rawlings, and John Yin. “Stochastic Kinetic Modeling
of Vesicular Stomatitis Virus Intracellular Growth”. English. In: Bulletin of
Mathematical Biology 71.7 (2009), pp. 1671–1692. issn: 0092-8240.
[17] H. Solari J. Aparicio. “Population dynamics: Poisson approximation and its relation
to the langevin process”. In: Physical Review Letters (2001), p. 4183.
[18] Hye-Won Kang and Thomas G Kurtz. “Separation of time-scales and model
reduction for stochastic reaction networks”. In: (2013).
[19] Diederik P Kingma and Jimmy Ba. “Adam: A method for stochastic optimization”.
In: arXiv preprint arXiv:1412.6980 (2014).
[20] Hiroyuki Kuwahara and Ivan Mura. “An efficient and exact stochastic simulation
method to analyze rare events in biochemical systems”. In: The Journal of chemical
physics 129.16 (2008), 10B619.
[21] Christopher V Rao and Adam P Arkin. “Stochastic chemical kinetics and the
quasi-steady-state assumption: Application to the Gillespie algorithm”. In: The
Journal of chemical physics 118.11 (2003), pp. 4999–5010.
39

References IV
[22] Elijah Roberts et al. “Noise Contributions in an Inducible Genetic Switch: A
Whole-Cell Simulation Study”. In: PLoS computational biology 7 (Mar. 2011),
e1002010. doi: 10.1371/journal.pcbi.1002010.
[23] Sophia Wiechert. “Optimal Control of Importance Sampling Parameters in Monte
Carlo Estimators for Stochastic Reaction Networks”. MA thesis. 2021.
40

KAUST_talk_short.pdf

More Related Content

Similar to KAUST_talk_short.pdf

More from Chiheb Ben Hammouda

Recently uploaded

KAUST_talk_short.pdf