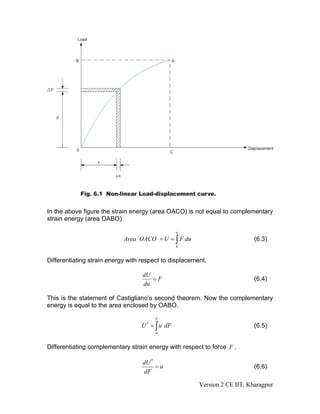
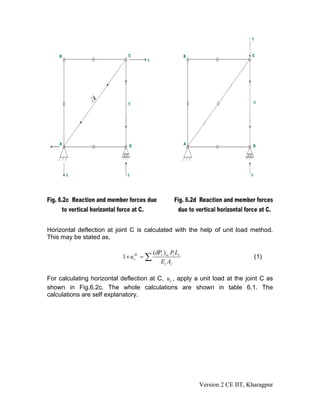
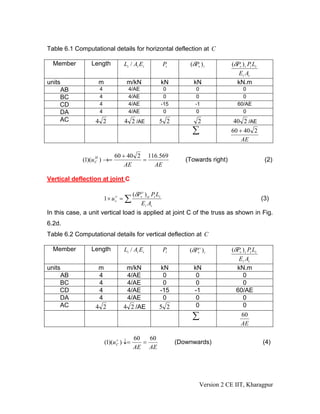
This document discusses Engesser's theorem and calculating truss deflections using the virtual work principle. It introduces Engesser's theorem, which relates the derivative of complementary strain energy to displacement. It then derives equations for calculating truss deflections due to external loads, temperature loads, and fabrication errors using the unit load method. Several examples are provided to demonstrate calculating truss joint deflections for different load cases.