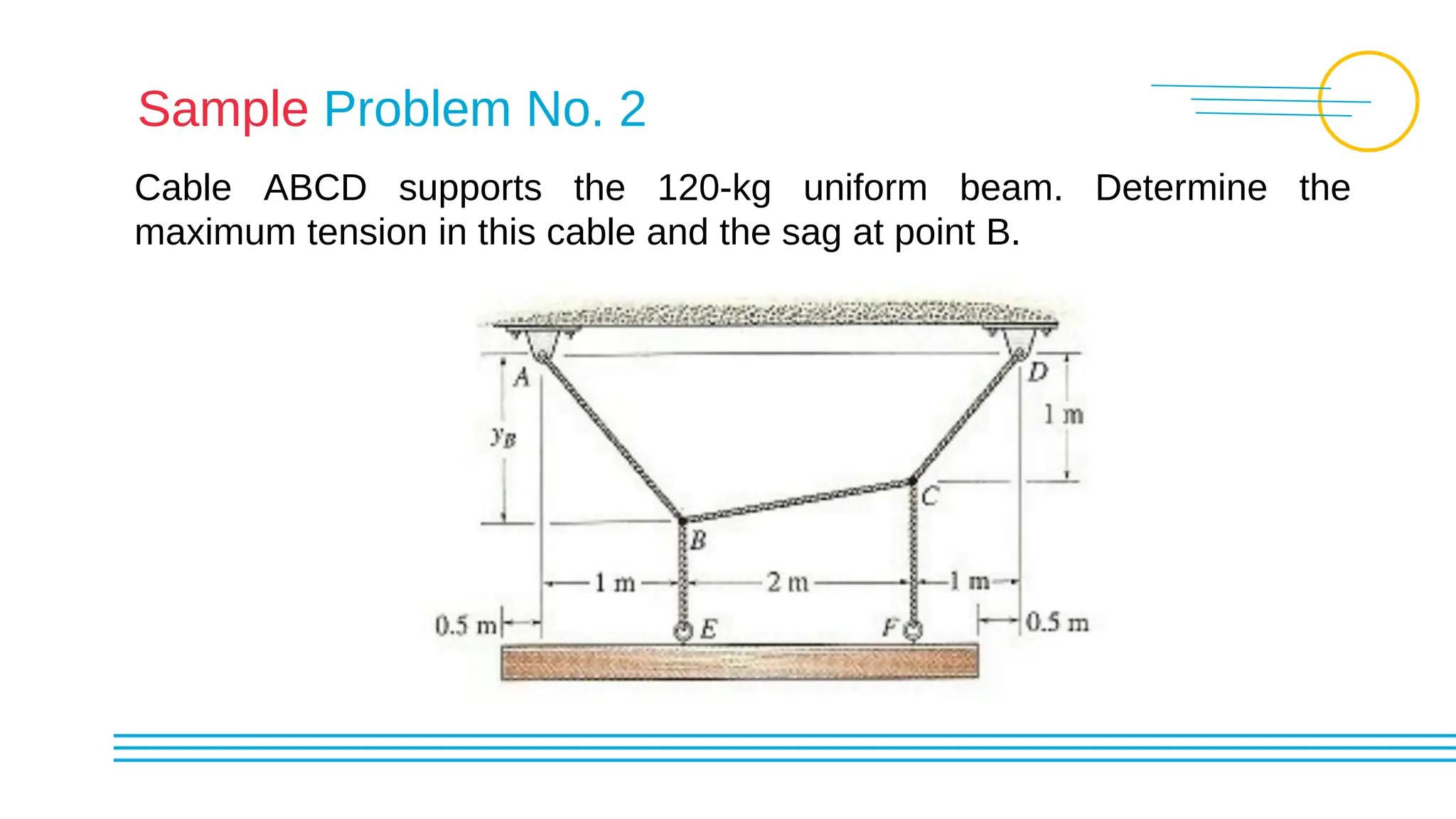
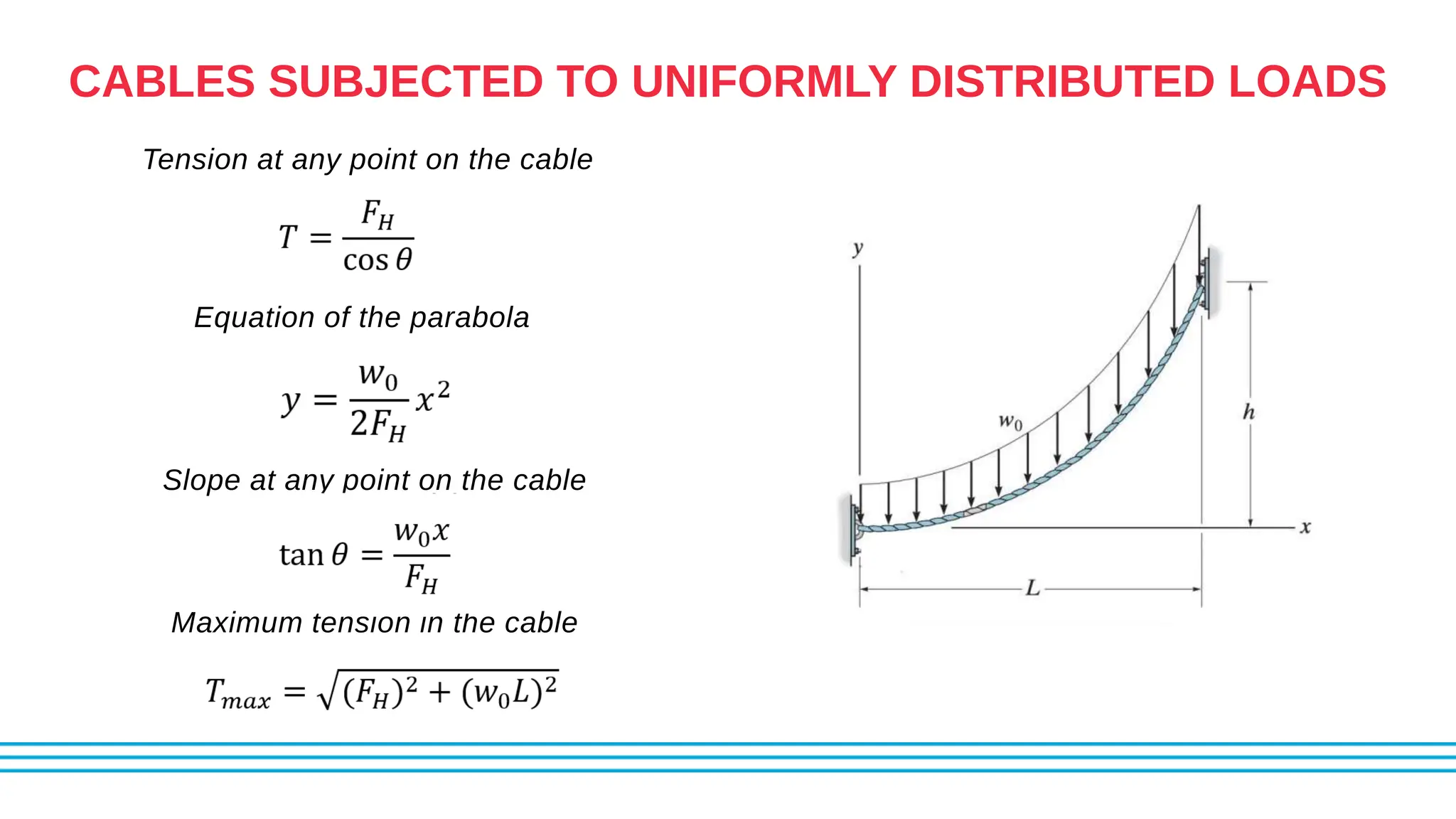
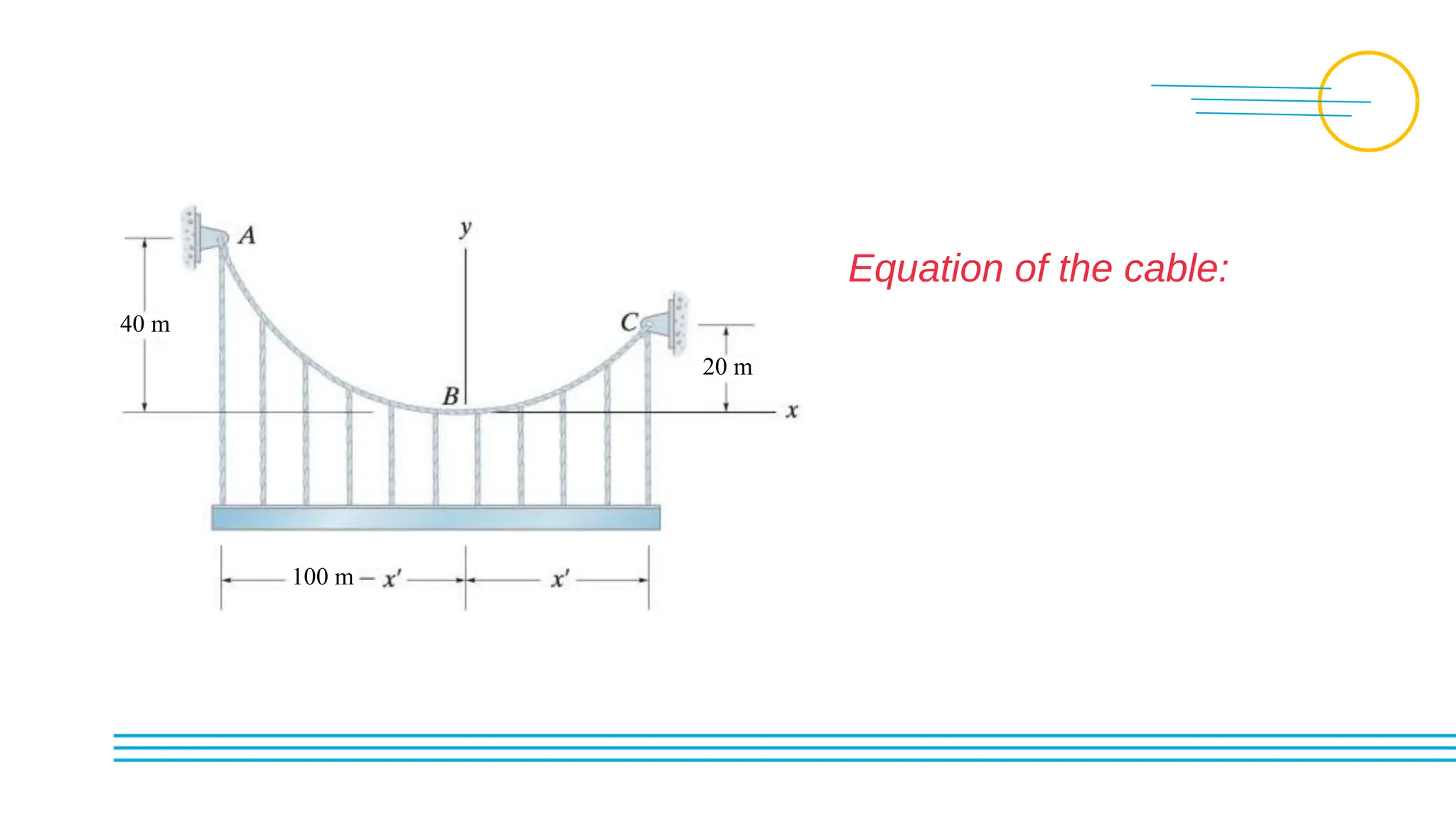
This document discusses the structural theory of cables and arches, including methods for analyzing statically determinate cables and arches. It provides examples of how to determine tensions in cable segments under concentrated and uniformly distributed loads, as well as the reactions of three-hinged arches under concentrated loads. Sample problems demonstrate calculating tensions, sags, and support reactions for various cable and arch configurations.

1. CABLES and
ARCHES
STRUCTURAL THEORY CIV 0314 - 4

2. Methods of Analysis for Statically
Determinate Cables and Arches
a. Cables Subjected to Concentrated Load
b. Cables Subjected to Uniform Distributed Loads
c. Three-Hinged Arch

3. CABLES
are often used in engineering
structures for support and to transmit
loads from one member to another.
When used to support suspension
roofs, bridges, and trolley wheels,
cables form the main load-carrying
element in the structure.

4. Brooklyn Bridge Akashi-Kaikyo Bridge

5. Cables are perfectly flexible, resistance to shear and bending
is small and may be neglected.
Cables’ Assumptions
01
02
03
By means of cable flexibility, the force acting in the cable is
always tangent to the cable at the point along its length.
Cables are inextensible, its length is constant for both before
and after the load is applied.

6. CABLES SUBJECTED TO
CONCENTRATED LOADS
When a cable of negligible weight
supports several concentrated
loads, the cable takes the form of
several straight-line segments,
each of which is subjected to
constant tensile force.

7. Determine the value of h and the tension in each segment of the cable
shown.
Sample Problem No. 1

8. Solution:

9. at Point C:

10. at Point B:

11. SOLVING FOR h:

12. Sample Problem No. 2
Cable ABCD supports the 120-kg uniform beam. Determine the
maximum tension in this cable and the sag at point B.

13. Consider the beam
SOLUTION: Solving for CF
Solving for BE

14. Solving for D = CD

15. Solving for A = AB

16. SOLVING FOR y
B

17. Sample Problem No. 3
The cable supports the loading shown. Determine the magnitude of the horizontal
force P so that x = 6m.
2 m
2 m
8 m
5 m
400 N

18. Solution:
Joint B:
TAB
400 lb
TBC
2 17
2 17
2
2
8
8

19. Joint C:
P
TBC
61
2 17
5
2
8
6

20. CABLES SUBJECTED TO
UNIFORMLY DISTRIBUTED LOADS
Cables subjected to uniformly
distributed loads are called parabolic
cables. If a cable supports vertical load
only, the horizontal component () of the
cable tension is constant at all sections
along the axis of the cable. The
maximum tension occurs at supports
where the cable slop is largest.

21. CABLES SUBJECTED TO UNIFORMLY DISTRIBUTED LOADS
Tension at any point on the cable
Equation of the parabola
Slope at any point on the cable
Maximum tension in the cable

22. Sample Problem No. 4
The cable is subjected to a uniform loading of w = 60 kN/m. Determine
the maximum and minimum tension in cable.

23. Solution:

24. Sample Problem No. 5
The cable in the figure supports a girder which weighs 850 N/m.
Determine the tension in the cable at points A, B, and C.
100 m
40 m
20 m

25. Equation of the cable:
40 m
100 m
20 m

26. At point C, x = x’
At point A, x = 100 - x’
40 m
100 m
20 m

27. Slope equation:
At point A, x = -58.58
40 m
100 m
20 m

28. At point B, x = 0
At point C, x = 41.42
20 m
100 m
40 m

29. The suspension bridge in the figure is constructed using the two stiffening trusses that are pin
connected at their ends C and supported by a pin at A and a rocker at B. Determine the
minimum and maximum tensions and the uniform load in the cable IH. The cable has a
parabolic shape, and the bridge is subjected to the single load of 50 kN.
Sample Problem No. 6

33. Arches
Arches can be used to reduce the bending
moments in long-span structures. Essentially, an
arch acts as an inverted cable, so it receives its
load mainly in compression although, because of
its rigidity, it must also resist some bending and
shear depending upon how it is loaded and
shaped. Arches are used for buildings where large
clear spans are required such as gymnasiums,
churches, warehouse, & conventional halls.

34. A three-hinged arch is subjected to two concentrated loads, as shown in the
figure. Determine the support reactions of the arch.
Sample Problem No. 7

35. Consider the whole arch: Consider the segment CE:

36. Solving for Ex and Ey:
Solving for Ax and Ay:

37. The three-hinged tied arch is subjected to the loading shown in the figure. Determine the
force in members CH and CB. The dashed member GF of the truss is intended to carry no
force.
Sample Problem No. 8

38. Support Reactions:

39. Free body diagram of the left part of the arch:

40. Isolate joint G: Isolate joint C:

41. Sample Problem No. 9
Determine the magnitudes of the resultant forces at pin A,B and C of the three hinged-
arched roof truss.

42. Solution:

43. Solution:

44. Solution:

45. Solution:

46. “Dreams are the trusses of our
ambitions, the beams of our
determination, and the cables
that lift us to new heights. Keep
building, keep rising.”
Corocotchia, R.B.D, Gallarte, A.C., Licayan, J.Z., Venturina, R.A.V.