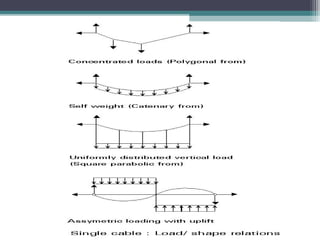
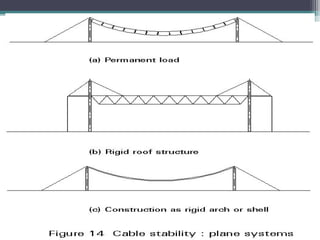
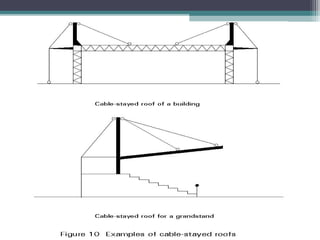
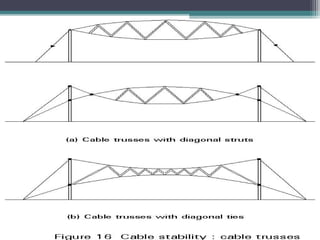
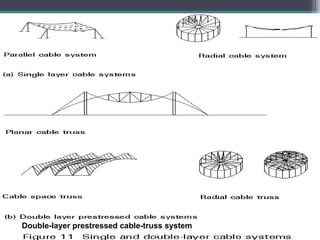
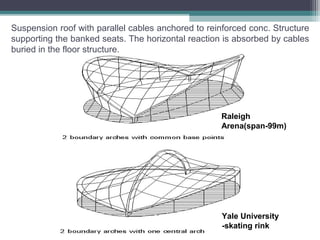
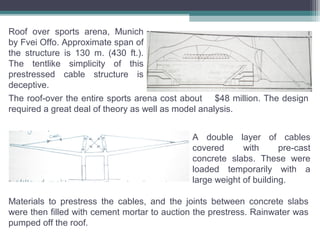
The document discusses cable structures and their role as form-active systems that transmit loads through tension and compression. It highlights the design considerations, advantages, and limitations of cable systems, including their adaptability to loads, stability issues, and applications in modern architecture such as sports arenas and bridges. The importance of materials, particularly steel, and structural elements in optimizing cable systems for large spans is also emphasized.

1. CABLE
STRUCTURE
S

2. CABLE SYSTEMS
MAJOR SYSTEM → FORM ACTIVE STRUCTURE
SYSTEMS.
→ Non rigid, flexible matter
shaped in a certain way and secured by fixed ends, an support
itself & span space. The transmit loads only through simple
normal stresses; either tension or through compression.
Two cables with different points of suspension tied
together form a suspension system. A cable subject to external
loads will deform in a way depending upon the magnitude and
location of the external forces. The form acquired by the cable
is called the FUNICULAR SHAPE of the cable.
# Form Active Structure Systems redirect external
forces by simple normal stresses : the arch by compression,
the suspension cable by tension. The bearing mechanism of
form active systems vests essentially on the material form.

3. # The natural stress line of the form active tension
system in the funicular tension line.
# Any change of loading or support conditions
changes the form of the funicular curve.
Form active systems because of their dependence on
loading conditions are strictly governed by the natural ‘flow of
forces’ and hence cannot become subject to arbitrary free
form design.

4. LOADING MECHANISM :
# The high tensile strength of steel, combined with the
efficiency of simple tension, makes a steel cable the ideal
structural element to span large distances.
# Cables are flexible because o their large shall lateral
dimensions in relation to their lengths. As uneven stresses true
to bending are prevented by flexibility the tensile load is evenly
divided among the cable strands.
In order to understand the mechanism by means of
which a cable supports vertical loads, one may first consider a
cable suspended between two fixed points, located at the
same level and carrying a single load at mid span. Under the
action of the load the cable assumes a symmetrical triangular
shape and half the load is carried to each support by simple
tension along he two halves of the cable.

5. CABLE SAG :
The triangular shape acquired by the cable is
characterized by the SAG : the vertical distance between the
supports and the lowest point in the cable. Without the sag the
cable cannot carry the load, since the tensile forces in if would
be horizontal and horizontal forces cannot balance the vertical
load. The undivided pull of the sagging cable on each support
may be split into two components :
• a downward force equal to half the load
• a horizontal inward pull or thrust.
The thrust is inversely proportional to the sag; halving
the sag doubles the thrust. This raises an interesting question
of economy through.

6. OPTIMAL SAG :
A large sag increases the
cable length, but reduces the tensile
force & allows a reduction of cross-
section. A similar sag requires a
larger cross-section. Hence the total
volume of cable (product of cross-
section & length), must be minimum
for some optimal value of sag →
Optimal sag equal half the
span for a given horizontal distance
& corresponds to a symmetrical 45
o
–
triangle cable configuration with
thrust = p/2.

7. FUNICULAR POLYGONS :
# As the number of loads increases, the funicular polygon approaches a
geometrical curve – the PARABOLA large number of loads are evenly
spaced horizontally.
CATENARY :
If the equal loads are distributed evenly along the length of the cable, rather
than horizontally, the funicular curve differs from a parabola, through it has
the same general configuration. It is a catenary.
A cable carrying its own weight ad a loads evenly distributed horizontally,
acquires a shape that is intermediate between a parabola & catenary. This
is the shape of cables in the central span of suspension bridges.
GEOMETRIC FUNICULAR FORMS :
If the load is shifted from mid span position, the cable changes shape.
# If two equal loads are set on the cable in symmetrical positions the cable
adapts itself by acquiring a new configuration with three straight video.

9. SPECIAL DESIGN CONSIDERATIONS:
(And Corrective Measures)
Lightness of the flexible suspension cable is the demerit of the
system, which can be largely eliminated through pre-stressing so that
it can receive frictional forces that also may be upward directed.
Cable structures are more correctly categorize into either suspension
structures or cable-stayed structured suspension structures can be
typically sub-classified into :
1. Single Curvature Structures
2. Double Curvature Structures
3. Double Cable Structures
A critical problem in the design of any cable roof structure is the
dynamic effect of wind, which causes an undesirable fluttering of the
roof.
DYNAMIC EFFECTS OF WIND ON TYPICAL
FLEXIBLE ROOF STRUCTURE :

10. PREVENTIVE MEASURES :
There are only several fundamental ways to combat
flutter.
• One is to simply increase the deal load on the roof.
• Another is to provide anchoring guy cables at periodic
points to tie the structure to the ground.
• To use some sort of crossed cable on double-cable
system.The principal methods of providing stability are the
following:
(i) Additional permanent load supported on, or suspended from, the roof,
sufficient to neutralize the effects of asymmetrical variable actions or uplift
Figure 14a).
This arrangement has the drawback that it eliminates the lightweight
nature of the structure, adding significant cost to the entire structure.
(ii) Rigid members acting as beams, where permanent load may not be
adequate to counteract uplift forces completely, but where there is
sufficient flexural rigidity to deal with the net uplift forces, whilst availing of
cables to help resist effects of gravity loading (Figure 14b).

13. LIMITATIONS DUE TO VIBRATIONS &
CHANGING LOADS :
The limitations in the application of cables stem directly
from their adaptability to changing loads : CABLES are
unstable and stability is one of the basic requirements of
structural systems. The trusses hanging from the cables of a
suspension bridge not only support the roadway but also
stiffen the cables against motions due to moving or changing
loads.

14. STIFFENING TRUSSES :
Stiffening trusses are
usually rigid in the direction of
bridge axis, but less so in
transverse directions. Modern
suspension bridges are made
sage against lateral wind
displacements by using
stiffening GUY WIRES OR
STAYS which have the
double role of supporting the
truss & stabilizing it.
A cable truss system has a triangulated structural form
which increases stiffness, particularly under non-symmetric
loading.

16. Double-layer prestressed cable-truss system

17. DESIGN OF SUPPORTING ELEMENTS :
In addition to actual roof cables, other structural elements
egs: masts, guy cables are needed to make a building structure.
The elements typically support the cable in space and provide
means of transferring its vertical & horizontal thrusts to the ground.
The design of these elements is as crucial as the cable design.
APPLICATIONS OF CABLE SYSTEMS :
The earliest use of cables in buildings dates back to A.D. 70
to roof a Roman amphitheater by a rope cable structure. Rope
cables anchored to masts spanned in a radial fashion across the
open structure supported a movable sunshade that could be drawn
across to cover the arena. The span was 620 ft. along major axis
and 513 ft. along minor axis.

18. Today the longest suspension bridge has a span of 1410 m. (4226 ft.); the
longest suspension roof; the Burgo Paper Mill in Mantcia has a span of 163
m. (535 ft.). The roof was designed like a suspension bridge. The cable
flexibility is not wholly advantageous as in bridge. Excessive vibrations can
not be tolerated in a building. Water proofing of the roof is difficult. Most
suspension roofs are therefore prestressed to reduce their flexibility & some
also have concrete roofs.
The first modern roof was an Arena. Load bearing cables are suspended
from two intersecting arches, anchored against one another. At night
angles to the load bearing are secondary cables prestressed to ensure
tautness even on a hot day. Corrugated sheets supported on the cable
network.

19. Raleigh
Arena(span-99m)
Yale University
-skating rink
Suspension roof with parallel cables anchored to reinforced conc. Structure
supporting the banked seats. The horizontal reaction is absorbed by cables
buried in the floor structure.

20. Structures using suspended cables have a functional advantage for arenas,
because the shape is better suited to an array of banked seats than that of a
dome. A suspension roof requires a smaller volume of air than a dome. This
can produce imp. economics in air-conditioning & heating.
Memorial Auditorium in Litica, New York. Span –
73 m (240 ft.). Two sets of cables, are separated
by struts that cause them to act in conjunction. The
amount of prestress for upper and lower cables
varied. Vibrations in one set of cables are different
or out of phase with the other and the opposing
forces damp the vibration of the structure.

21. Roof over sports arena, Munich
by Fvei Offo. Approximate span of
the structure is 130 m. (430 ft.).
The tentlike simplicity of this
prestressed cable structure is
deceptive.
The roof-over the entire sports arena cost about $48 million. The design
required a great deal of theory as well as model analysis.
A double layer of cables
covered with pre-cast
concrete slabs. These were
loaded temporarily with a
large weight of building.
Materials to prestress the cables, and the joints between concrete slabs
were then filled with cement mortar to auction the prestress. Rainwater was
pumped off the roof.

22. Cable-stiffened cantilever roof. The structure is several
100% stronger than the cantilever on its own. The cable
provides the tensile component of the resistant moment, so
that the cantilever becomes the compression member, and
the distance between the cantilever & cable of the support
provides the lever arm of the resistance moment.
Other applications of cable structures can be for
exhibition pavilions, sports complexes, army shelters etc.
Cables can be used to increase the span of cantilevers and is
particularly useful for aircraft hangars and other buildings than
require large entrances as well as unobstructed interior span.

23. MATERIALS :
Steel, nylon ropes or plasticated cables may be used for
different structures.
• Steel Cables : The high tensile strength of steel
combined with the efficiency of simple tension, makes a steel
cable the ideal structural element to span large distances.
• Nylon and plastics are suitable only for temporary
structures, spanning small distances.
other structural members like masts, compression rings,
arches or beams and compression struts may be of concrete
or steel preferably. Struts may also be of timber.
Suspension Cables, because of their being stressed
only by simple tension – with regard to weight/span are the
most economical system of spanning space.

24. Because of their identity with the natural flow of forces,
the form active structure system is a suitable mechanism for
achieving long spans and forming large spaces.
Suspension cables are the elementary idea for any
bearing mechanism and consequently the very symbol of
man’s technical Seizure of space.
Before of their long span qualities, they have a particular
significance for mass civilization and its demand for large
scale spaces. They are potential structure forms for future
building.