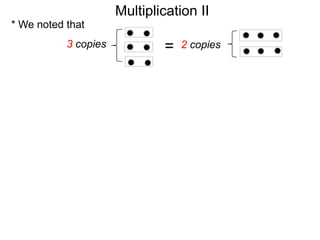
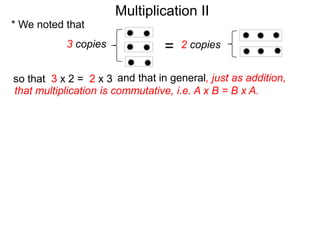
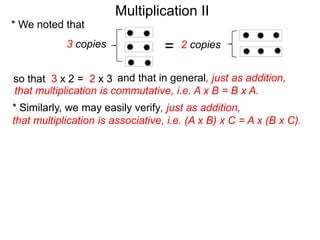
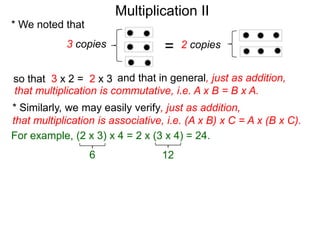
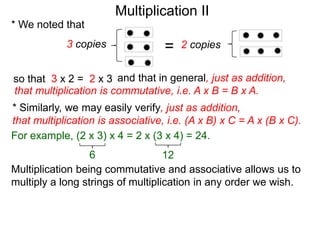
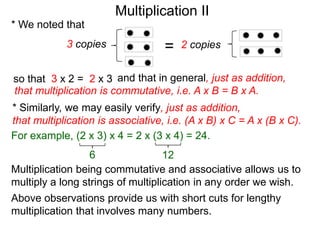
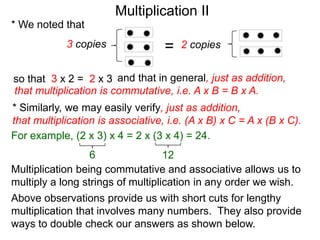
The document discusses properties of multiplication, including: - The product of zero with any number is 0, so 0 is the "annihilator" in multiplication. - The product of 1 with any number x is x, so 1 is the "preserver" in multiplication. - Multiplication is commutative (A x B = B x A) and associative ((A x B) x C = A x (B x C)), allowing numbers to be multiplied in any order. - For lengthy multiplications, it is recommended to multiply in pairs to obtain the answer more efficiently.

1. Multiplication II
http://www.lahc.edu/math/frankma.htm

2. Multiplication II
In the last section we covered the arithmetic mechanics of
multiplying two numbers in the vertical format where in modern
day most of this work is delegated to calculators or software.

3. Multiplication II
In the last section we covered the arithmetic mechanics of
multiplying two numbers in the vertical format where in modern
day most of this work is delegated to calculators or software.
In mathematics, we are also interested in the properties and
relations.

4. Multiplication II
In the last section we covered the arithmetic mechanics of
multiplying two numbers in the vertical format where in modern
day most of this work is delegated to calculators or software.
In mathematics, we are also interested in the properties and
relations.
Properties of Multiplication

5. Multiplication II
In the last section we covered the arithmetic mechanics of
multiplying two numbers in the vertical format where in modern
day most of this work is delegated to calculators or software.
In mathematics, we are also interested in the properties and
relations.
Properties of Multiplication
We note from before before that
* (0 * x = 0 * x = 0) The product of zero with any number is 0.

6. Multiplication II
In the last section we covered the arithmetic mechanics of
multiplying two numbers in the vertical format where in modern
day most of this work is delegated to calculators or software.
In mathematics, we are also interested in the properties and
relations.
Properties of Multiplication
We note from before before that
* (0 * x = 0 * x = 0) The product of zero with any number is 0.
In other words, 0 is the “annihilator” in multiplication.
It demolishes anything multiplied with it .

7. Multiplication II
In the last section we covered the arithmetic mechanics of
multiplying two numbers in the vertical format where in modern
day most of this work is delegated to calculators or software.
In mathematics, we are also interested in the properties and
relations.
Properties of Multiplication
We note from before before that
* (0 * x = 0 * x = 0) The product of zero with any number is 0.
In other words, 0 is the “annihilator” in multiplication.
It demolishes anything multiplied with it .
For example, A*B*0*C = 0 where A, B ,and C are numbers.

8. Multiplication II
In the last section we covered the arithmetic mechanics of
multiplying two numbers in the vertical format where in modern
day most of this work is delegated to calculators or software.
In mathematics, we are also interested in the properties and
relations.
Properties of Multiplication
We note from before before that
* (0 * x = 0 * x = 0) The product of zero with any number is 0.
In other words, 0 is the “annihilator” in multiplication.
It demolishes anything multiplied with it .
For example, A*B*0*C = 0 where A, B ,and C are numbers.
* (1 * x = x * 1 = x) The product of 1 with any number x is x.

9. Multiplication II
In the last section we covered the arithmetic mechanics of
multiplying two numbers in the vertical format where in modern
day most of this work is delegated to calculators or software.
In mathematics, we are also interested in the properties and
relations.
Properties of Multiplication
We note from before before that
* (0 * x = 0 * x = 0) The product of zero with any number is 0.
In other words, 0 is the “annihilator” in multiplication.
It demolishes anything multiplied with it .
For example, A*B*0*C = 0 where A, B ,and C are numbers.
* (1 * x = x * 1 = x) The product of 1 with any number x is x.
In other words, 1 is the “preserver” in multiplication,
It preserves anything multiplies with it .

10. Multiplication II
In the last section we covered the arithmetic mechanics of
multiplying two numbers in the vertical format where in modern
day most of this work is delegated to calculators or software.
In mathematics, we are also interested in the properties and
relations.
Properties of Multiplication
We note from before before that
* (0 * x = 0 * x = 0) The product of zero with any number is 0.
In other words, 0 is the “annihilator” in multiplication.
It demolishes anything multiplied with it .
For example, A*B*0*C = 0 where A, B ,and C are numbers.
* (1 * x = x * 1 = x) The product of 1 with any number x is x.
In other words, 1 is the “preserver” in multiplication,
It preserves anything multiplies with it .
For example, A*1*B*1*C = A*B*C.

11. Multiplication II
* We noted that
3 copies
=
2 copies

12. Multiplication II
* We noted that
3 copies
=
2 copies
so that 3 x 2 = 2 x 3 and that in general, just as addition,
that multiplication is commutative, i.e. A x B = B x A.

13. Multiplication II
* We noted that
3 copies
=
2 copies
so that 3 x 2 = 2 x 3 and that in general, just as addition,
that multiplication is commutative, i.e. A x B = B x A.
* Similarly, we may easily verify, just as addition,
that multiplication is associative, i.e. (A x B) x C = A x (B x C).

14. Multiplication II
* We noted that
3 copies
=
2 copies
so that 3 x 2 = 2 x 3 and that in general, just as addition,
that multiplication is commutative, i.e. A x B = B x A.
* Similarly, we may easily verify, just as addition,
that multiplication is associative, i.e. (A x B) x C = A x (B x C).
For example, (2 x 3) x 4 = 2 x (3 x 4) = 24.
6
12

15. Multiplication II
* We noted that
3 copies
=
2 copies
so that 3 x 2 = 2 x 3 and that in general, just as addition,
that multiplication is commutative, i.e. A x B = B x A.
* Similarly, we may easily verify, just as addition,
that multiplication is associative, i.e. (A x B) x C = A x (B x C).
For example, (2 x 3) x 4 = 2 x (3 x 4) = 24.
6
12
Multiplication being commutative and associative allows us to
multiply a long strings of multiplication in any order we wish.

16. Multiplication II
* We noted that
3 copies
=
2 copies
so that 3 x 2 = 2 x 3 and that in general, just as addition,
that multiplication is commutative, i.e. A x B = B x A.
* Similarly, we may easily verify, just as addition,
that multiplication is associative, i.e. (A x B) x C = A x (B x C).
For example, (2 x 3) x 4 = 2 x (3 x 4) = 24.
6
12
Multiplication being commutative and associative allows us to
multiply a long strings of multiplication in any order we wish.
Above observations provide us with short cuts for lengthy
multiplication that involves many numbers.

17. Multiplication II
* We noted that
3 copies
=
2 copies
so that 3 x 2 = 2 x 3 and that in general, just as addition,
that multiplication is commutative, i.e. A x B = B x A.
* Similarly, we may easily verify, just as addition,
that multiplication is associative, i.e. (A x B) x C = A x (B x C).
For example, (2 x 3) x 4 = 2 x (3 x 4) = 24.
6
12
Multiplication being commutative and associative allows us to
multiply a long strings of multiplication in any order we wish.
Above observations provide us with short cuts for lengthy
multiplication that involves many numbers. They also provide
ways to double check our answers as shown below.

18. Multiplication II
i. For a lengthy multiplication, multiply in pairs.

19. Multiplication II
i. For a lengthy multiplication, multiply in pairs.
For example, 2 x 4 x 3 x 5 = (2 x 4) x (3 x 5)

20. Multiplication II
i. For a lengthy multiplication, multiply in pairs.
For example, 2 x 4 x 3 x 5 = (2 x 4) x (3 x 5) = 8 x 15 = 120

21. Multiplication II
i. For a lengthy multiplication, multiply in pairs.
For example, 2 x 4 x 3 x 5 = (2 x 4) x (3 x 5) = 8 x 15 = 120
12
or
2x3x4x5
10

22. Multiplication II
i. For a lengthy multiplication, multiply in pairs.
For example, 2 x 4 x 3 x 5 = (2 x 4) x (3 x 5) = 8 x 15 = 120
12
or
2 x 3 x 4 x 5 = 10 x 12 = 120
10

23. Multiplication II
i. For a lengthy multiplication, multiply in pairs.
For example, 2 x 4 x 3 x 5 = (2 x 4) x (3 x 5) = 8 x 15 = 120
12
or
2 x 3 x 4 x 5 = 10 x 12 = 120
10
Example A. a. Multiply 2 x 4 x 1 x 3 x 5 x 1 x 25.
Do it in two different orders to confirm the answer.

24. Multiplication II
i. For a lengthy multiplication, multiply in pairs.
For example, 2 x 4 x 3 x 5 = (2 x 4) x (3 x 5) = 8 x 15 = 120
12
or
2 x 3 x 4 x 5 = 10 x 12 = 120
10
Example A. a. Multiply 2 x 4 x 1 x 3 x 5 x 1 x 25.
Do it in two different orders to confirm the answer.
Drop the 1’s: 2 x 4 x 1 x 3 x 5 x 1 x 25 = 2 x 4 x 3 x 5 x 25

25. Multiplication II
i. For a lengthy multiplication, multiply in pairs.
For example, 2 x 4 x 3 x 5 = (2 x 4) x (3 x 5) = 8 x 15 = 120
12
or
2 x 3 x 4 x 5 = 10 x 12 = 120
10
ii. Look for “even numbers” x “multiples of 5”, these produce
“multiples of 10” with trailing 0’s.
Example A. a. Multiply 2 x 4 x 1 x 3 x 5 x 1 x 25.
Do it in two different orders to confirm the answer.
Drop the 1’s: 2 x 4 x 1 x 3 x 5 x 1 x 25 = 2 x 4 x 3 x 5 x 25
I.
2 x 4 x 3 x 5 x 25

26. Multiplication II
i. For a lengthy multiplication, multiply in pairs.
For example, 2 x 4 x 3 x 5 = (2 x 4) x (3 x 5) = 8 x 15 = 120
12
or
2 x 3 x 4 x 5 = 10 x 12 = 120
10
ii. Look for “even numbers” x “multiples of 5”, these produce
“multiples of 10” with trailing 0’s.
Example A. a. Multiply 2 x 4 x 1 x 3 x 5 x 1 x 25.
Do it in two different orders to confirm the answer.
Drop the 1’s: 2 x 4 x 1 x 3 x 5 x 1 x 25 = 2 x 4 x 3 x 5 x 25
10 100
I.
2 x 4 x 3 x 5 x 25

27. Multiplication II
i. For a lengthy multiplication, multiply in pairs.
For example, 2 x 4 x 3 x 5 = (2 x 4) x (3 x 5) = 8 x 15 = 120
12
or
2 x 3 x 4 x 5 = 10 x 12 = 120
10
ii. Look for “even numbers” x “multiples of 5”, these produce
“multiples of 10” with trailing 0’s.
Example A. a. Multiply 2 x 4 x 1 x 3 x 5 x 1 x 25.
Do it in two different orders to confirm the answer.
Drop the 1’s: 2 x 4 x 1 x 3 x 5 x 1 x 25 = 2 x 4 x 3 x 5 x 25
10 100
I.
2 x 4 x 3 x 5 x 25
= 3 x 10 x 100
= 3,000

28. Multiplication II
i. For a lengthy multiplication, multiply in pairs.
For example, 2 x 4 x 3 x 5 = (2 x 4) x (3 x 5) = 8 x 15 = 120
12
or
2 x 3 x 4 x 5 = 10 x 12 = 120
10
ii. Look for “even numbers” x “multiples of 5”, these produce
“multiples of 10” with trailing 0’s.
Example A. a. Multiply 2 x 4 x 1 x 3 x 5 x 1 x 25.
Do it in two different orders to confirm the answer.
Drop the 1’s: 2 x 4 x 1 x 3 x 5 x 1 x 25 = 2 x 4 x 3 x 5 x 25
10 100
II.
I.
50
2 x 4 x 3 x 5 x 25
= 3 x 10 x 100
= 3,000
2 x 4 x 3 x 5 x 25
20

29. Multiplication II
i. For a lengthy multiplication, multiply in pairs.
For example, 2 x 4 x 3 x 5 = (2 x 4) x (3 x 5) = 8 x 15 = 120
12
or
2 x 3 x 4 x 5 = 10 x 12 = 120
10
ii. Look for “even numbers” x “multiples of 5”, these produce
“multiples of 10” with trailing 0’s.
Example A. a. Multiply 2 x 4 x 1 x 3 x 5 x 1 x 25.
Do it in two different orders to confirm the answer.
Drop the 1’s: 2 x 4 x 1 x 3 x 5 x 1 x 25 = 2 x 4 x 3 x 5 x 25
10 100
II.
I.
50
2 x 4 x 3 x 5 x 25
= 3 x 10 x 100
= 3,000
2 x 4 x 3 x 5 x 25 = 20 x 3 x 50
= 3,000
20

30. Multiplication II
Even if there is no “easy picking” as in the previous example,
it’s shorter to multiply in pairs then multiply one-by-one in order.

31. Multiplication II
Even if there is no “easy picking” as in the previous example,
it’s shorter to multiply in pairs then multiply one-by-one in order.
b. Multiply 3 x 3 x 2 x 7 x 2. Do it in the order that’s given first,
then do it in pairs, to confirm the answer.

32. Multiplication II
Even if there is no “easy picking” as in the previous example,
it’s shorter to multiply in pairs then multiply one-by-one in order.
b. Multiply 3 x 3 x 2 x 7 x 2. Do it in the order that’s given first,
then do it in pairs, to confirm the answer.
Doing it in the order that’s given:
3x3x2x7x2

33. Multiplication II
Even if there is no “easy picking” as in the previous example,
it’s shorter to multiply in pairs then multiply one-by-one in order.
b. Multiply 3 x 3 x 2 x 7 x 2. Do it in the order that’s given first,
then do it in pairs, to confirm the answer.
Doing it in the order that’s given:
3x3x2x7x2
=9x2x7x2

34. Multiplication II
Even if there is no “easy picking” as in the previous example,
it’s shorter to multiply in pairs then multiply one-by-one in order.
b. Multiply 3 x 3 x 2 x 7 x 2. Do it in the order that’s given first,
then do it in pairs, to confirm the answer.
Doing it in the order that’s given:
3x3x2x7x2
=9x2x7x2
= 18 x 7 x 2

35. Multiplication II
Even if there is no “easy picking” as in the previous example,
it’s shorter to multiply in pairs then multiply one-by-one in order.
b. Multiply 3 x 3 x 2 x 7 x 2. Do it in the order that’s given first,
then do it in pairs, to confirm the answer.
Doing it in the order that’s given:
3x3x2x7x2
=9x2x7x2
= 18 x 7 x 2
= 136 x 2
= 272

36. Multiplication II
Even if there is no “easy picking” as in the previous example,
it’s shorter to multiply in pairs then multiply one-by-one in order.
b. Multiply 3 x 3 x 2 x 7 x 2. Do it in the order that’s given first,
then do it in pairs, to confirm the answer.
Doing it in the order that’s given:
Doing it in pairs:
3x3x2x7x2
(3 x 3) x (2 x 7) x 2
=9x2x7x2
= 18 x 7 x 2
= 136 x 2
= 272

37. Multiplication II
Even if there is no “easy picking” as in the previous example,
it’s shorter to multiply in pairs then multiply one-by-one in order.
b. Multiply 3 x 3 x 2 x 7 x 2. Do it in the order that’s given first,
then do it in pairs, to confirm the answer.
Doing it in the order that’s given:
Doing it in pairs:
3x3x2x7x2
(3 x 3) x (2 x 7) x 2
=9x2x7x2
= 9 x 14 x 2
= 18 x 7 x 2
= 136 x 2
= 272

38. Multiplication II
Even if there is no “easy picking” as in the previous example,
it’s shorter to multiply in pairs then multiply one-by-one in order.
b. Multiply 3 x 3 x 2 x 7 x 2. Do it in the order that’s given first,
then do it in pairs, to confirm the answer.
Doing it in the order that’s given:
Doing it in pairs:
3x3x2x7x2
(3 x 3) x (2 x 7) x 2
=9x2x7x2
= 9 x 14 x 2
= 18 x 7 x 2
= 136 x 2
= 272
= 9 x 28
= 272

39. Multiplication II
Even if there is no “easy picking” as in the previous example,
it’s shorter to multiply in pairs then multiply one-by-one in order.
b. Multiply 3 x 3 x 2 x 7 x 2. Do it in the order that’s given first,
then do it in pairs, to confirm the answer.
Doing it in the order that’s given:
Doing it in pairs:
3x3x2x7x2
(3 x 3) x (2 x 7) x 2
=9x2x7x2
= 9 x 14 x 2
= 18 x 7 x 2
= 136 x 2
= 272
We simplify the notation for
repetitive additions as:
3 copies
2+2+2=3x2
= 9 x 28
= 272

40. Multiplication II
Even if there is no “easy picking” as in the previous example,
it’s shorter to multiply in pairs then multiply one-by-one in order.
b. Multiply 3 x 3 x 2 x 7 x 2. Do it in the order that’s given first,
then do it in pairs, to confirm the answer.
Doing it in the order that’s given:
Doing it in pairs:
3x3x2x7x2
(3 x 3) x (2 x 7) x 2
=9x2x7x2
= 9 x 14 x 2
= 18 x 7 x 2
= 136 x 2
= 9 x 28
= 272
= 272
We simplify the notation for
repetitive additions as:
We simplify the notation for
repetitive multiplication as:
3 copies
3 copies
2+2+2=3x2
2 * 2 * 2 = 23 = 8

41. Multiplication II
About the Notation

42. Multiplication II
About the Notation
In the notation
23
=2*2*2 =8

43. Multiplication II
About the Notation
In the notation
this is the base
23
=2*2*2 =8

44. Multiplication II
About the Notation
In the notation
this is the base
this is the exponent,
or the power, which is
the number of repetitions.
23
=2*2*2 =8

45. Multiplication II
About the Notation
In the notation
this is the base
this is the exponent,
or the power, which is
the number of repetitions.
23
=2*2*2 =8
We say that “2 to the power 3 is 8” or
that “2 to the 3rd power is 8.”

46. Multiplication II
About the Notation
In the notation
this is the base
this is the exponent,
or the power, which is
the number of repetitions.
23
=2*2*2 =8
We say that “2 to the power 3 is 8” or
that “2 to the 3rd power is 8.”
Recall that for repetitive addition, we write
3 copies
2 + 2 + 2 as 3 x 2 = 3(2) = 2(3) with 3 to one the side.

47. Multiplication II
About the Notation
In the notation
this is the base
this is the exponent,
or the power, which is
the number of repetitions.
23
=2*2*2 =8
We say that “2 to the power 3 is 8” or
that “2 to the 3rd power is 8.”
Recall that for repetitive addition, we write
3 copies
2 + 2 + 2 as 3 x 2 = 3(2) = 2(3) with 3 to one the side.
So for repetitive multiplication, to distinguish it from addition,
we store the number of repetition in the upper corner.

48. Multiplication II
About the Notation
In the notation
this is the base
this is the exponent,
or the power, which is
the number of repetitions.
23
=2*2*2 =8
We say that “2 to the power 3 is 8” or
that “2 to the 3rd power is 8.”
Recall that for repetitive addition, we write
3 copies
2 + 2 + 2 as 3 x 2 = 3(2) = 2(3) with 3 to one the side.
So for repetitive multiplication, to distinguish it from addition,
we store the number of repetition in the upper corner.
Hence, we write 2 * 2 * 2 as 23.
3 copies

49. Multiplication II
Example B. Calculate the following.
a. 3(4)
d. 22 x 3
b. 34
e. 2 x 32
c. 43
f. 22 x 33

50. Multiplication II
Example B. Calculate the following.
a. 3(4)
= 12
d. 22 x 3
b. 34
e. 2 x 32
c. 43
f. 22 x 33

51. Multiplication II
Example B. Calculate the following.
a. 3(4)
= 12
d. 22 x 3
b. 34
= 3*3*3*3
e. 2 x 32
c. 43
f. 22 x 33

52. Multiplication II
Example B. Calculate the following.
a. 3(4)
= 12
b. 34
= 3*3*3*3
c. 43
= 9 * 9
d. 22 x 3
e. 2 x 32
f. 22 x 33

53. Multiplication II
Example B. Calculate the following.
a. 3(4)
= 12
b. 34
= 3*3*3*3
c. 43
= 9 * 9
= 81
d. 22 x 3
e. 2 x 32
f. 22 x 33

54. Multiplication II
Example B. Calculate the following.
a. 3(4)
= 12
b. 34
= 3*3*3*3
c. 43
=4*4*4
= 9 * 9
= 81
d. 22 x 3
e. 2 x 32
f. 22 x 33

55. Multiplication II
Example B. Calculate the following.
a. 3(4)
= 12
b. 34
= 3*3*3*3
= 9 * 9
= 81
d. 22 x 3
e. 2 x 32
c. 43
=4*4*4
= 16 * 4
= 64
f. 22 x 33

56. Multiplication II
Example B. Calculate the following.
a. 3(4)
= 12
b. 34
= 3*3*3*3
= 9 * 9
= 81
d. 22 x 3
= 2*2*3
= 12
e. 2 x 32
c. 43
=4*4*4
= 16 * 4
= 64
f. 22 x 33

57. Multiplication II
Example B. Calculate the following.
a. 3(4)
= 12
b. 34
= 3*3*3*3
= 9 * 9
= 81
d. 22 x 3
= 2*2*3
= 12
e. 2 x 32
= 2*3*3
c. 43
=4*4*4
= 16 * 4
= 64
f. 22 x 33

58. Multiplication II
Example B. Calculate the following.
a. 3(4)
= 12
b. 34
= 3*3*3*3
= 9 * 9
= 81
d. 22 x 3
= 2*2*3
= 12
e. 2 x 32
= 2*3*3
= 6*3
= 18
c. 43
=4*4*4
= 16 * 4
= 64
f. 22 x 33

59. Multiplication II
Example B. Calculate the following.
a. 3(4)
= 12
b. 34
= 3*3*3*3
= 9 * 9
= 81
d. 22 x 3
= 2*2*3
= 12
e. 2 x 32
= 2*3*3
= 6*3
= 18
c. 43
=4*4*4
= 16 * 4
= 64
f. 22 x 33
= 2*2*3*3*3

60. Multiplication II
Example B. Calculate the following.
a. 3(4)
= 12
b. 34
= 3*3*3*3
= 9 * 9
= 81
d. 22 x 3
= 2*2*3
= 12
c. 43
=4*4*4
= 16 * 4
= 64
e. 2 x 32
= 2*3*3
f. 22 x 33
= 2*2*3*3*3
= 6*3
= 18
= 4 *9 *3

61. Multiplication II
Example B. Calculate the following.
a. 3(4)
= 12
b. 34
= 3*3*3*3
= 9 * 9
= 81
d. 22 x 3
= 2*2*3
= 12
c. 43
=4*4*4
= 16 * 4
= 64
e. 2 x 32
= 2*3*3
f. 22 x 33
= 2*2*3*3*3
= 6*3
= 18
= 4 *9 *3
= 36 * 3
= 108

62. Multiplication II
Example B. Calculate the following.
a. 3(4)
= 12
b. 34
= 3*3*3*3
= 9 * 9
= 81
d. 22 x 3
= 2*2*3
= 12
c. 43
=4*4*4
= 16 * 4
= 64
e. 2 x 32
= 2*3*3
f. 22 x 33
= 2*2*3*3*3
= 6*3
= 18
= 4 *9 *3
= 36 * 3
= 108
Problems d, c and e are the same as 22(3), 2(32), and 22(33).