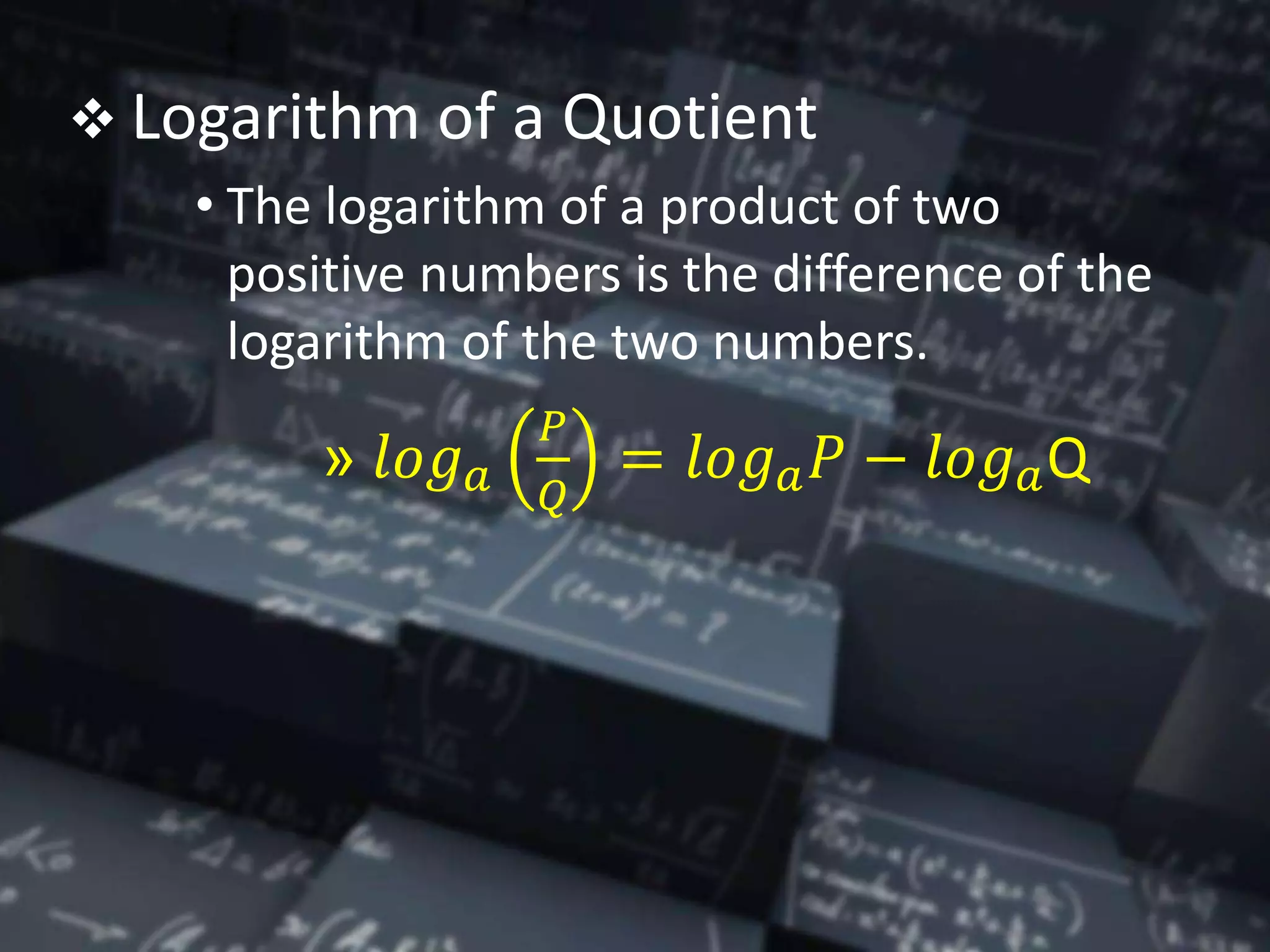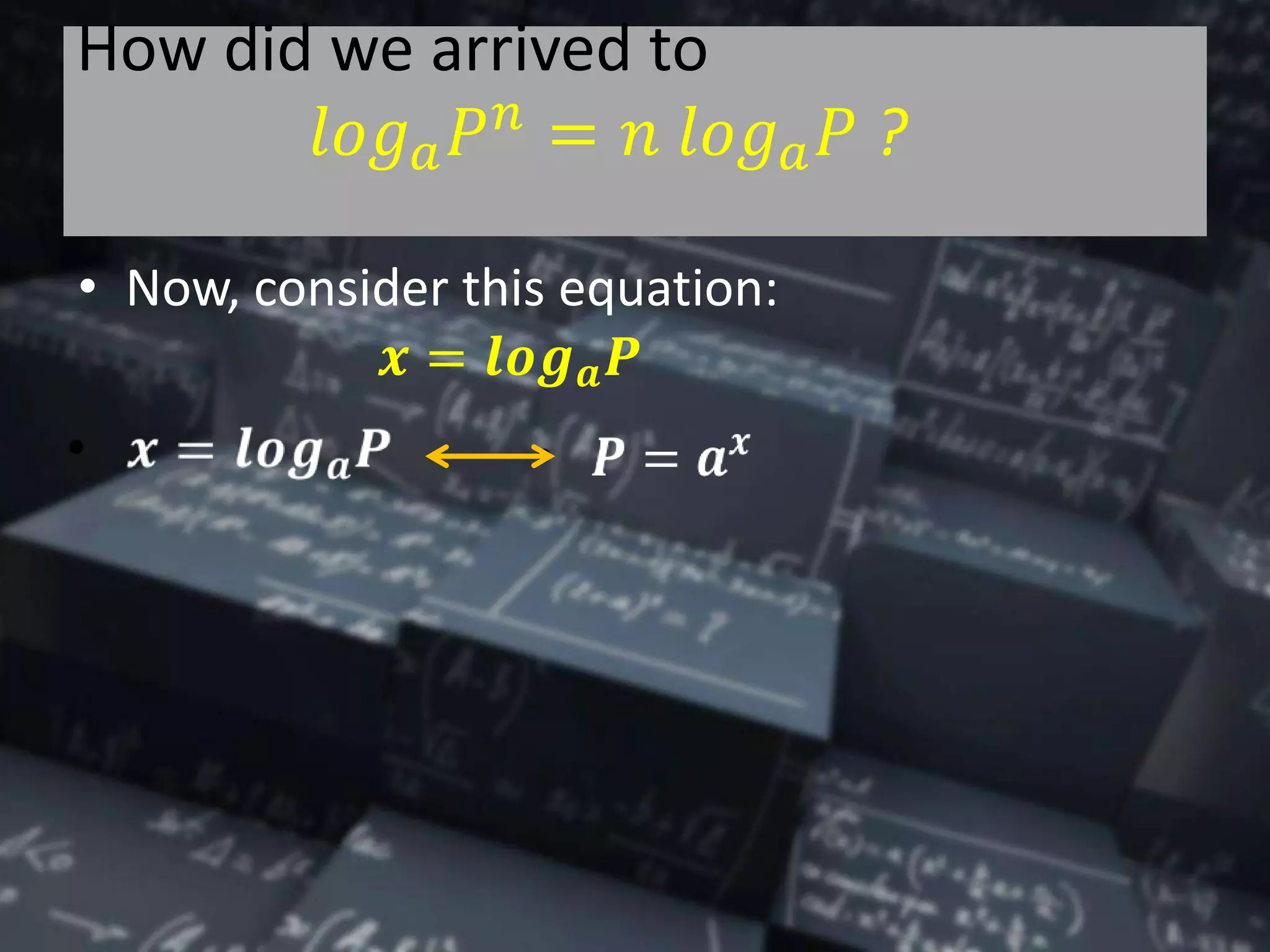A logarithm is the power to which a number must be raised to get another number. The logarithm of a product is the sum of the logarithms of the factors. The logarithm of a quotient is the logarithm of the numerator minus the logarithm of the denominator. The logarithm of a power is that power times the logarithm of the number. Natural logarithms use e as the base and are written as ln. Logarithms between 1 and 10 are called mantissas and consist of a characteristic, an integer, and a mantissa, a decimal.

1. L O G A R I T H M

2. WHAT IS LOGARITHM?
• A logarithm is the power to which a
number must be raised in order to get
some other number
𝒊𝒇 𝒚 = 𝒃 𝒙
, 𝒕𝒉𝒆𝒏 𝒍𝒐𝒈 𝒃 𝒚 = 𝒙.
Exponential form Logarithmic form

3. Example
• The logarithm of 100 to the base 10 is 2.
100 = 102
because 𝑙𝑜𝑔10100 = 2

4. Laws of Logarithms
 Logarithm of a Product
• The logarithm of a product of two
positive numbers is the sum of the
logarithms of two numbers.
𝒍𝒐𝒈 𝒂 𝑷𝑸 = 𝒍𝒐𝒈 𝒂 𝑷 + 𝒍𝒐𝒈 𝒂 𝑸

5. How did we arrived to this logarithmic
form; 𝒍𝒐𝒈 𝒂 𝑷𝑸 = 𝒍𝒐𝒈 𝒂 𝑷 + 𝒍𝒐𝒈 𝒂 𝑸 ?
• consider these equations:
𝒙 = 𝒍𝒐𝒈 𝒂 𝑷 and 𝒚 = 𝒍𝒐𝒈 𝒂 𝑸
• 𝒙 = 𝒍𝒐𝒈 𝒂 𝑷 𝑷 = 𝒂 𝒙
• 𝒚 = 𝒍𝒐𝒈 𝒂 𝑸 𝑸 = 𝒂 𝒚

6.  Logarithm of a Quotient
• The logarithm of a product of two
positive numbers is the difference of the
logarithm of the two numbers.
» 𝑙𝑜𝑔 𝑎
𝑃
𝑄
= 𝑙𝑜𝑔 𝑎 𝑃 − 𝑙𝑜𝑔 𝑎Q

7. How did we arrived to this logarithmic form;
𝑙𝑜𝑔 𝑎
𝑃
𝑄
= 𝑙𝑜𝑔 𝑎 𝑃 − 𝑙𝑜𝑔 𝑎Q ?
• Similarly, consider the same equations,
𝒙 = 𝒍𝒐𝒈 𝒂 𝑷 and 𝒚 = 𝒍𝒐𝒈 𝒂 𝑸
• 𝒙 = 𝒍𝒐𝒈 𝒂 𝑷 𝑷 = 𝒂 𝒙
• 𝒚 = 𝒍𝒐𝒈 𝒂 𝑸 𝑸 = 𝒂 𝒚

8.  Logarithm of a Power
•The logarithm of the nth power of a
positive number is n times the
logarithm of the number.
𝑙𝑜𝑔 𝑎 𝑃 𝑛
= 𝑛 𝑙𝑜𝑔 𝑎 𝑃

9. How did we arrived to
𝑙𝑜𝑔 𝑎 𝑃 𝑛
= 𝑛 𝑙𝑜𝑔 𝑎 𝑃 ?
• Now, consider this equation:
𝒙 = 𝒍𝒐𝒈 𝒂 𝑷

10. NATURAL LOGARITHM
• A natural logarithm has a base of 𝑒. • We
write natural logarithms as ln.
– In other words, 𝑙𝑜𝑔 𝑒x = ln 𝑥.

12. CHARACTERISTIC AND MANTISSA
The logarithms of numbers between 1 and 10
are called mantissas. They are what are given
(approximately) in a table of logarithms. They
are all positive decimals, since 10 must be
raised to some positive power less than 1 to
give a number between 1 and 10. In a table of
mantissas, we find: 10 log 1.476 =.169

13. • therefore, log 1476 = log10 log1.476 3 .169
3.169. = + =+ = When the logarithm of any
number is written in this way, the integer is called
its characteristic and the decimal is called its
mantissa. Note that logarithms of numbers which
differ only in the position of the decimal point all
have the same mantissa. log14.76 log10 1.476
1.169 = × = 2 log147.6 log10 1.476 2.169. = ×=
When the number is less than 1, the
characteristic will be negative. 3 log.001476 log10
1.476 3 .169 2.831.