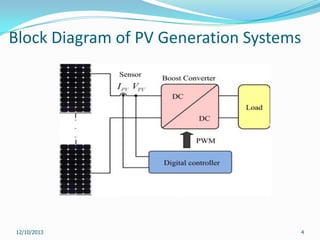
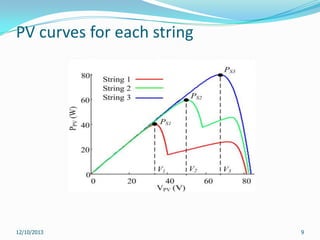
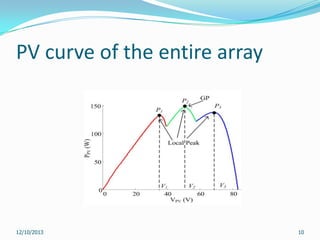
This document reviews maximum power point tracking (MPPT) algorithms for photovoltaic systems. It discusses conventional MPPT techniques like perturb and observe and incremental conductance. It also examines intelligent MPPT techniques using fuzzy logic, artificial neural networks, particle swarm optimization, ant colony optimization, and firefly algorithms. The firefly algorithm is proposed as suitable for partial shaded conditions due to its ability to find the global maximum power point. The document concludes that while conventional MPPT methods have limitations, intelligent techniques have merits and drawbacks, and further research is needed.

1. Paper Code: 134
A Review of Maximum Power Point Tracking
Algorithms for Photovoltaic Systems under
Uniform and Non-Uniform irradiances
12/10/2013
1

2. by
T.LOGESWARAN
Assistant Professor(SRG)
Department of EEE
Kongu Engineering College,
Perundurai, Erode, Tamilnadu, India
Dr.A.SENTHIL KUMAR, M.E.,PhD.,
Prof & Head, Department of EEE
Dr.Mahalingam College of Engineering and Technology,
Pollachi, Tamilnadu, India
12/10/2013
2

3. Introduction
Why Solar PV power systems?
 maintenance free
 noise free
 environmental friendly
12/10/2013
3

4. Block Diagram of PV Generation Systems
12/10/2013
4

5. Modelling of PV module
 Two diode model with seven parameters
 Two diode model with five parameters
Two Diode model of the PV cell
12/10/2013
5

6. Two Diode model of the PV cell
12/10/2013
6

7. simplified
Series Parallel combination of the PV array
12/10/2013
7

8. Characteristics of PV Cell under PSC
Operation of PV array under partial shading
12/10/2013
8

9. PV curves for each string
12/10/2013
9

10. PV curve of the entire array
12/10/2013
10

11. CONVENTIONAL MPPT TECHNIQUES
 Perturb and Observe





Hill Climbing algorithm
Incremental Conductance
short circuit current
open circuit voltage and
ripple correlation control approaches
12/10/2013
11

12. Intelligent MPPT Techniques
FLC based MPPT
 Mamdanis method is used for fuzzy inference
 Centre of gravity method for defuzzification
and the duty ratio is computed
 fuzzy rule base, which is dependent on the
experience of algorithm developers –
influences on the performance of MPPT
12/10/2013
12

13. Artificial Neural Network
based MPPT
It is suitable for the system that can get sufficient training
data
12/10/2013
13

14. PSO based MPPT
Demerits:
• It is incapable of searching maxima
• local convergence accuracy is not high
12/10/2013
14

15. ACO based MPPT
The number of ants (M), Convergence speed (€), Solution
archive (K) and Locality of search process (Q) ---- these
parameters are to decided by the user
When choosing the number of ants, there will be tradeoff
between convergence speed and tracking accuracy
12/10/2013
15

16. Firefly algorithm
 Firefly algorithm is a bio inspired metaheuristic
algorithm for optimization problems
 Introduced in 2009 at Cambridge University by Yang
Rules for constructing firefly algorithm:
1) All fireflies are unisex
2) Brightness of the firefly is determined from the
encoded objective function
3) Attractiveness is directly proportional to brightness
but decreases with distance and a firefly will move
towards the brighter one and if there is no brighter
one, it will move randomly.
12/10/2013
16

17. 12/10/2013
17

18. Firefly alorithm
The algorithm can be summarized as follows:
I.
II.
III.
IV.
V.
Generate a random solution set, {x1, x2, . . . xk}
Compute intensity for each solution
member,{I1, I2, ……. Ik}
Move each firefly i towards other brighter
fireflies and if there is no other brighter firefly,
move it randomly
Update the solution set
Terminate if a termination criterion is fulfilled
other wise go back to stepII.
12/10/2013
18

19. Conclusion:
 Conventional MPPT algorithms does not find the
global maxima. Intelligent MPPT techniques have
merits and demerits. It is concluded that FA based
MPPT will be suitable for partial shaded conditions.
12/10/2013
19

20. References. .
1.
2.
3.
4.
Bidyadhar Subudhi and Raseswari Pradhan (2013) “A Comparative
Study on Maximum Power Point Tracking Techniques for Photov
oltaic Power Systems” IEEE Transactions on Sustainable Energy,V
ol. 4, No. 1
Moacyr Aureliano Gomes de Brito, Luigi Galotto,(2013) Jr.,
Leonardo Poltronieri Sampaio, Guilherme de Azevedo e Melo,
and Carlos Alberto Canesin, Senior Member, “Evaluation of the
Main MPPT Techniques for Photovoltaic Applications” IEEE
Transactions on Industrial Electronics, VOL. 60, NO. 3.
M. A. S. Masoum, H. Dehbonei, and E. F. Fuchs, 2002
“Theoretical and experimental analyses of photovoltaic systems
with voltage and current based maximum power point tracking,”
IEEE Trans. Energy Conv., vol. 17, no. 4, pp. 514–522
B. Subudhi and R. Pradhan, 2011 “Characteristics evaluation and
parameter extraction of a solar array based on experimental
analysis,” in Proc. 9th IEEE Power Electron. Drives Syst.,
Singapore
12/10/2013
20

21. References
[T. Esram, J. W. Kimball, P. T. Krein, P. L. Chapman, and P.
Midya, (2006) “Dynamic maximum power point tracking of
photovoltaic arrays using ripple correlation control,” IEEE
Trans. Power Electron., vol. 21, no.5, pp. 1282–1291
6. K. Ishaque, Z. Salam, and H. Taheri,(2011) “Simple, fast and
accurate two diode model for photovoltaic modules,” Solar
Energy Mater. Solar Cells, vol. 95, pp. 586–594
7. K. Ishaque, Z. Salam, and H. Taheri,(2011) “Accurate
MATLAB simulink PV system simulator based on a twodiode model,” J. Power Electron., vol. 11, pp. 179–187
8. Kashif Ishaque, Zainal Salam, Muhammad Amjad, and
Saad Mekhilef,( 2012) “An Improved Particle Swarm
Optimization (PSO)–Based MPPT for PV With Reduced
Steady-State Oscillation” IEEE transactions on Power
Eelectronics, vol. 27, no. 8
5.
12/10/2013
21

22. References
9. MASAFUMI MIYATAKE, MUMMADI VEERACHARY,
NOBUHIKO FUJII, HIDEYOSHI KO , (2011) “ Maximum Power
Point Tracking of Multiple Photovoltaic Arrays: A PSO Approach”
IEEE Transactions on Aerospace and Electronic Systems VOL. 47,
NO. 1.
10. Yi-Hwa Liu, Shyh-Ching Huang, Jia-Wei Huang, and Wen-Cheng
Liang (2012) “A Particle Swarm Optimization-Based Maximum
Power Point Tracking Algorithm for PV Systems Operating Under
Partially Shaded Conditions” IEEE Transactions on Energy
Conversion, VOL. 27, NO. 4.
11. Mahmoud A. YOUNIS , Tamer KHATIB, Mushtaq NAJEEB, A
Mohd ARIFFIN (2012), An Improved Maximum Power Point
Tracking Controller for PV Systems Using Artificial Neural
Network Przegląd Elektrotechniczny, R. 88 NR 3b
12. Whei-Min Lin, Member, IEEE, Chih-Ming Hong, and ChiungHsing Chen 2011, “Neural-Network-Based MPPT Control of a
Stand-Alone Hybrid Power Generation System” IEEE Transactions
on Power Electronics, VOL. 26, NO. 12.
12/10/2013
22

23. 13. Lian Lian Jiang, Douglas L. Maskell, Jagdish C. Patra (2013), A
14.
15.
16.
17.
Novel Ant Colony optimization based maximum power point t
racking for photovoltaic systems under partially shaded conditi
ons, Energy and Buildings Vol 58. Pgs 227-236.
N. Chai-ead, P. Aungkulanon, and P. Luangpaiboon, Member, I
AENG (2011), Bees and Firefly Algorithms for Noisy Non-Linear
Optimization Problems Proceedings of the 26th International
multi Conference of engineers andComputer ScientistsVolume I
I.
Surafel Luleseged Tilahun and Hong Choon Ong(2012) “Modifi
ed Firefly Algorithm” Hindawi Publishing Corporation, Journa
l of Applied Mathematics, Article ID 467631, 12 pages
A. Mathew and A. I. Selvakumar, (2006) “New MPPT for PV arr
ays using fuzzy controller in close cooperation with fuzzy cogni
tive network,” IEEE Trans. Energy Conv., vol. 21, no. 3, pp. 793
–803.
C.-S. Chiu, (2010)“T-S fuzzy maximum power point tracking co
ntrol of solar power generation systems,” IEEE Trans. Energy C
onv., vol. 25, no. 4, pp. 1123–1132.
12/10/2013
23

24. THANK YOU
12/10/2013
24