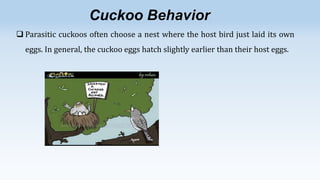
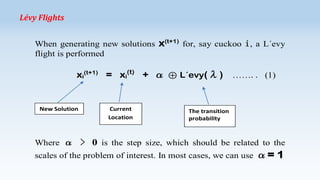
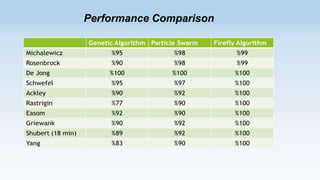
The document summarizes two nature-inspired metaheuristic algorithms: the Cuckoo Search algorithm and the Firefly algorithm. The Cuckoo Search algorithm is based on the brood parasitism of some cuckoo species. It lays its eggs in the nests of other host birds. The algorithm uses Lévy flights for generating new solutions and considers the best solutions for the next generation. The Firefly algorithm is based on the flashing patterns of fireflies to attract mates. It considers attractiveness that decreases with distance and movement of fireflies towards more attractive ones. The pseudo codes of both algorithms are provided along with some example applications.

1. Cuckoo Search & Firefly
Algorithms
By: Mustafa Salam

2. Cuckoo Search Algorithm

3. Overview
Cuckoo search (CS) is an optimization algorithm developed by Xin-she Yang
and Suash Deb in 2009.
Cuckoos have an aggressive reproduction strategy that involves the female
laying her fertilized eggs in the nest of another species so that the surrogate
parents unwittingly raise her brood. Sometimes the cuckoo's egg in the host
nest is discovered (eggs are not its owns), the surrogate parents either throw
it out or abandon the nest and builds their own brood elsewhere.

4. Cuckoo Behavior
 Some cuckoo species have evolved in such a way that female parasitic
cuckoos are often very specialized in the mimicry in color and pattern of
the eggs of a few chosen host species. This reduces the probability of eggs
being abandoned and increases their reproductively.

5. Cuckoo Behavior
 Parasitic cuckoos often choose a nest where the host bird just laid its own
eggs. In general, the cuckoo eggs hatch slightly earlier than their host eggs.

6. Cuckoo Behavior
 Once the first cuckoo chick is hatched, the first instinct action it will take is
to evict the host eggs by blindly propelling the eggs out of the nest, which
increases the cuckoo chick’s share of food provided by its host bird.

7. Cuckoo Rules & Parameters
1)
Each cuckoo lays one egg at a time, and dumps it in a randomly chosen nest.
2)
The best nests with high quality of eggs (solutions) will carry over to the next
generations.
3)
The number of available host nests is fixed, and a host can discover an alien
egg with a probability pa ∈ [0, 1]. In this case, the host bird can either throw
the egg away or abandon the nest so as to build a completely new nest in a
new location.

8. •
As a further approximation, this last assumption can be approximated by a
fraction pa of the n nests being replaced by new nests (with new random
solutions at new locations).
•
For a maximization problem, the quality or fitness of a solution can simply
be proportional to the objective function. Other forms of fitness can be defined
in a similar way to the fitness function in genetic algorithms.

9. Lévy Flights
A Lévy flight is a random walk in which the step-lengths are distributed according
to a heavy-tailed probability distribution. After a large number of steps, the
distance from the origin of the random walk tends to a stable distribution.

10. Lévy Flights
When generating new solutions
flight is performed
x(t+1) for, say cuckoo i, a L´evy
xi(t+1) = xi(t) + α ⊕ L´evy(λ)
New Solution
Current
Location
…….. (1)
The transition
probability
Where α > 0 is the step size, which should be related to the
scales of the problem of interest. In most cases, we can use
α= 1

11. Lévy Flights
L v flig tses n lly p v eara d mwlk w ileth ir ra d m
´e y h se tia ro id
no a h
e no
s p a d w fro aL v d trib tio fo la es p
te s re ra n m ´e y is u n r rg te s
L´evy ∼ u = t−λ, (1 < λ ≤ 3)
……… (2)
Which has an infinite variance with an infinite mean. Here the steps essentially form a
random walk process with a power-law step-length distribution with a heavy tail. Some
of the new solutions should be generated by L´evy walk around the best
solution obtained so far, this will speed up the local search.

12. Lévy Flights
However, a substantial fraction of the new solutions should be generated by far field
randomization and whose locations should be far enough from the current best
solution, this will make sure the system will not be trapped in a local optimum.

13. Pseudo code of Cuckoo Search algorithm
Begin
Objective function f(x), x = (x1, ..., xd)T ;
Initial a population of n host nests xi (i = 1, 2, ..., n);
while (t <MaxGeneration) or (stop criterion)
Get a cuckoo (say i) randomly by Lévyflights;
Evaluate its quality/fitness Fi;
Choose a nest among n (say j) randomly;
if (Fi > Fj)
Replace j by the new solution;
end
Abandon a fraction (pa) of worse nests and build new ones at
new locations via L´evy flights;
Keep the best solutions (or nests with quality solutions);
Rank the solutions and find the current best;
end while
Postprocess results and visualization;
End

14. Cuckoo Applications
a)
Spring design and Welded beam design problems.
b)
Solve nurse scheduling problem.
c)
An efficient computation for data fusion in wireless sensor networks.
d)
A new quantum-inspired cuckoo search was developed to solve Knapsack
problems.
e)
Efficiently generate independent test paths for structural software testing
and test data generation.
f)
Applied to train neural networks with improved performance.

15. Firefly Algorithm

16. Firefly Algorithm
The firefly algorithm (FA) is a metaheuristic algorithm, developed by Xin-She
Yang in late 2007 and 2008 , which was based on the flashing patterns and
behavior of fireflies.

17. Behavior of Fireflies
There are about two thousand firefly species, and most fireflies produce short and
rhythmic flashes.

The pattern of flashes is often unique for a particular species. The flashing light is
produced by a process of bioluminescence, and the true functions of such
signaling systems are still debating.

However, two fundamental functions of such flashes are to attract mating
partners (communication), and to attract potential prey.

18. Behavior of Fireflies

In addition, flashing may also serve as a protective warning mechanism.

The rhythmic flash, the rate of flashing and the amount of time form part of
the signal system that brings both sexes together.

Females respond to a male’s unique pattern of flashing in the same
species, while in some species such as photuris, female fireflies can mimic the
mating flashing pattern of other species so as to lure and eat the male fireflies
who may mistake the flashes as a potential suitable mate.

19. Firefly Rules & Parameters

Fireflies are unisex so that one firefly will be attracted to other fireflies
regardless of their sex.

The attractiveness is proportional to the brightness, and they both decrease as
their distance increases. Thus for any two flashing fireflies, the less brighter
one will move towards the brighter one. If there is no brighter one than a
particular firefly, it will move randomly.

The brightness of a firefly is determined by the landscape of the objective
function.

20. Firefly Rules & Parameters

The light intensity at a particular distance (r) from the light source obeys
the inverse square law. That is to say , the light intensity (I) decreases as the
distance (r) increases in terms of ( I ∝ 1/ r2 ).

Furthermore, the air absorbs light which becomes weaker and weaker as
the distance increases.

21. The algorithm
In the firefly algorithm, there are three important formulas in firefly
algorithm, which are:

Attractiveness
The form of attractiveness function of a firefly is the following monotonically
decreasing function.
r
Where
e
rm
m 1
r is the distance between any two fireflies,
is a fixed light absorption coefficient.
…………
(1)
is the attractiveness at
r = 0
and

22. The algorithm

Distance
The distance between any two fireflies i and j at Xi and Xj, respectively, is the
Cartesian distance as follows:
Where xi,k is the (k)th component of the spatial coordinate Xi of (i)th firefly and d
is the number of dimensions.

23. The algorithm

Movement
The movement of a firefly i is attracted to another more attractive (brighter)
firefly j is determined by following equation:
Where the second term is due to the attraction while the third
term is ran d omi zati on wi th
being the randomization
parameter. rand is a random number generator uniformly
distributed in [0, 1]. For most cases in the implementation,
1 and
0,1 .
0

24. Pseudo code of the firefly algorithm
Begin
Objective function f (x), x = (x1 , ..., xd )T
Generate initial population of fireflies xi (i = 1, 2, ..., n)
Light intensity Ii at xi is determined by f ( xi )
Define light absorption coefficient γ
while (t <MaxGeneration)
for i = 1 : n all n fireflies
for j = 1 : i all n fireflies ( inner loop )
if ( Ij > Ii )
Move firefly i towards j ;
end if
Attractiveness varies with distance r via e−γr
Evaluate new solutions and update light intensity
end for j
end for i
Rank the fireflies and find the current best
end while
Postprocess results and visualization
End

25. Performance Comparison

26. Firefly Applications

Digital Image Compression and Image Processing

Feature selection

Antenna Design

Structural Design

Scheduling

Clustering

27. References
[1] Xin-She Yang, Suash Deb: “Nature-Inspired Metaheuristic Algorithms”, Luniver
Press, (2008).
[2] Nitesh Sureja ,”New Inspirations in Nature: A Survey “, G H Patel College of
Engineering & Technology, Vallabh Vidyanagar (Gujarat), INDIA (2012).
[3] Shakti Kumar, Parvinder Kaur, Amarpartap Singh,” Fuzzy Model Identification: A
Firefly Optimization Approach”, Department of Electronics & Communications,
SLIET, Longowal, Punjab, INDIA(2012).

28. Thank You