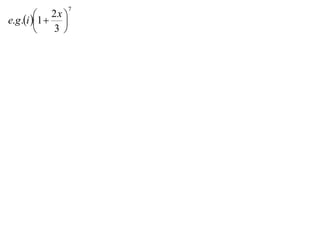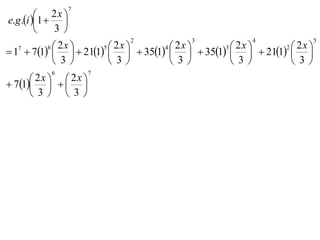The document discusses the binomial theorem, which provides a formula for expanding binomial expressions of the form (a + b)^n into a sum involving terms with coefficients given by the binomial coefficients from Pascal's triangle. As examples, the expansion of (x + 1)^7 and the use of the binomial theorem to find the expansion of (0.998 + 0.002x)^10 are shown.

1. Binomial Theorem

2. Binomial TheoremBinomial Expansions
A binomial expression is one which contains two terms.

3. Binomial TheoremBinomial Expansions
A binomial expression is one which contains two terms.
  11
0
 x

4. Binomial TheoremBinomial Expansions
A binomial expression is one which contains two terms.
  11
0
 x
  xx 111
1


5. Binomial TheoremBinomial Expansions
A binomial expression is one which contains two terms.
  11
0
 x
  xx 111
1

  22
1211 xxx 

6. Binomial TheoremBinomial Expansions
A binomial expression is one which contains two terms.
  11
0
 x
  xx 111
1

  22
1211 xxx 
    
32
322
23
331
221
12111
xxx
xxxxx
xxxx




7. Binomial TheoremBinomial Expansions
A binomial expression is one which contains two terms.
  11
0
 x
  xx 111
1

  22
1211 xxx 
    
32
322
23
331
221
12111
xxx
xxxxx
xxxx



    
432
43232
324
4641
33331
33111
xxxx
xxxxxxx
xxxxx




8. Blaise Pascal saw a pattern which we now know as Pascal’s Triangle

9. Blaise Pascal saw a pattern which we now know as Pascal’s Triangle
1

10. Blaise Pascal saw a pattern which we now know as Pascal’s Triangle
1
1 1

11. Blaise Pascal saw a pattern which we now know as Pascal’s Triangle
1
1 1
1 2 1

12. Blaise Pascal saw a pattern which we now know as Pascal’s Triangle
1
1 1
1 2 1
1 3 3 1

13. Blaise Pascal saw a pattern which we now know as Pascal’s Triangle
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1

14. Blaise Pascal saw a pattern which we now know as Pascal’s Triangle
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1

15. Blaise Pascal saw a pattern which we now know as Pascal’s Triangle
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1

16. Blaise Pascal saw a pattern which we now know as Pascal’s Triangle
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1

17. Blaise Pascal saw a pattern which we now know as Pascal’s Triangle
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1

18. Blaise Pascal saw a pattern which we now know as Pascal’s Triangle
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1

19. Blaise Pascal saw a pattern which we now know as Pascal’s Triangle
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
1 10 45 120 210 252 210 120 45 10 1

20.  
7
3
2
1.. 






x
ige

21.  
7
3
2
1.. 






x
ige
         
 
76
5
2
4
3
3
4
2
567
3
2
3
2
17
3
2
121
3
2
135
3
2
135
3
2
121
3
2
171












































xx
xxxxx

22.  
7
3
2
1.. 






x
ige
         
 
76
5
2
4
3
3
4
2
567
3
2
3
2
17
3
2
121
3
2
135
3
2
135
3
2
121
3
2
171












































xx
xxxxx
2187
128
729
448
243
672
81
560
27
280
9
84
3
14
1
765432
xxxxxxx


23.  
7
3
2
1.. 






x
ige
         
 
76
5
2
4
3
3
4
2
567
3
2
3
2
17
3
2
121
3
2
135
3
2
135
3
2
121
3
2
171












































xx
xxxxx
2187
128
729
448
243
672
81
560
27
280
9
84
3
14
1
765432
xxxxxxx

      dps8to0.998ofvaluethefindto1ofexpansiontheUse
1010
xii 

24.  
7
3
2
1.. 






x
ige
         
 
76
5
2
4
3
3
4
2
567
3
2
3
2
17
3
2
121
3
2
135
3
2
135
3
2
121
3
2
171












































xx
xxxxx
2187
128
729
448
243
672
81
560
27
280
9
84
3
14
1
765432
xxxxxxx

      dps8to0.998ofvaluethefindto1ofexpansiontheUse
1010
xii 
 
109
876543210
10
45120210252210120451011
xx
xxxxxxxxx



25.  
7
3
2
1.. 






x
ige
         
 
76
5
2
4
3
3
4
2
567
3
2
3
2
17
3
2
121
3
2
135
3
2
135
3
2
121
3
2
171












































xx
xxxxx
2187
128
729
448
243
672
81
560
27
280
9
84
3
14
1
765432
xxxxxxx

      dps8to0.998ofvaluethefindto1ofexpansiontheUse
1010
xii 
 
109
876543210
10
45120210252210120451011
xx
xxxxxxxxx


       3210
002.0120002.045002.0101998.0 

26.  
7
3
2
1.. 






x
ige
         
 
76
5
2
4
3
3
4
2
567
3
2
3
2
17
3
2
121
3
2
135
3
2
135
3
2
121
3
2
171












































xx
xxxxx
2187
128
729
448
243
672
81
560
27
280
9
84
3
14
1
765432
xxxxxxx

      dps8to0.998ofvaluethefindto1ofexpansiontheUse
1010
xii 
 
109
876543210
10
45120210252210120451011
xx
xxxxxxxxx


       3210
002.0120002.045002.0101998.0 
98017904.0

27.     42
5432inoftcoefficientheFind xxxiii 

28.     42
5432inoftcoefficientheFind xxxiii 
  
               432234
4
5544546544432
5432
xxxxx
xx



29.     42
5432inoftcoefficientheFind xxxiii 
  
               432234
4
5544546544432
5432
xxxxx
xx



30.     42
5432inoftcoefficientheFind xxxiii 
  
               432234
4
5544546544432
5432
xxxxx
xx



31.     42
5432inoftcoefficientheFind xxxiii 
  
               432234
4
5544546544432
5432
xxxxx
xx


         54435462oftcoefficien
3222
 x

32.     42
5432inoftcoefficientheFind xxxiii 
  
               432234
4
5544546544432
5432
xxxxx
xx


         54435462oftcoefficien
3222
 x
960
38404800



33.     42
5432inoftcoefficientheFind xxxiii 
  
               432234
4
5544546544432
5432
xxxxx
xx


         54435462oftcoefficien
3222
 x
Exercise 5A; 2ace etc, 4, 6, 7, 9ad, 12b, 13ac, 14ace, 16a, 22, 23
960
38404800

