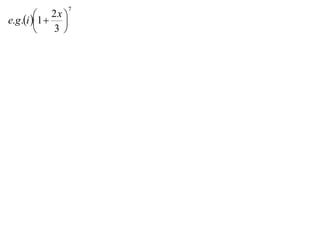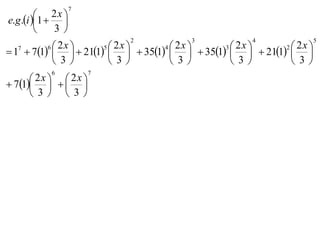The document discusses the binomial theorem and binomial expansions. It provides examples of expanding binomial expressions (1 + x)n up to n = 10 using Pascal's triangle. The expansions follow a pattern of coefficients that are the entries in Pascal's triangle. The document also gives an example of using the binomial expansion of (1 - x)10 to calculate the value of (0.998)10 to 8 decimal places.

1. Binomial Theorem

2. Binomial Theorem
Binomial Expansions
A binomial expression is one which contains two terms.

3. Binomial Theorem
Binomial Expansions
A binomial expression is one which contains two terms.
1  x 0  1

4. Binomial Theorem
Binomial Expansions
A binomial expression is one which contains two terms.
1  x 0  1
1  x 1  1  1x

5. Binomial Theorem
Binomial Expansions
A binomial expression is one which contains two terms.
1  x 0  1
1  x 1  1  1x
1  x 2  1  2 x  1x 2

6. Binomial Theorem
Binomial Expansions
A binomial expression is one which contains two terms.
1  x 0  1
1  x 1  1  1x
1  x 2  1  2 x  1x 2
1  x   1  x 1  2 x  1x 2 
3
 1  2 x  x 2  x  2 x 2  x3
 1  3x  3x 2  x 3

7. Binomial Theorem
Binomial Expansions
A binomial expression is one which contains two terms.
1  x 0  1
1  x 1  1  1x
1  x 2  1  2 x  1x 2
1  x   1  x 1  2 x  1x 2 
3
 1  2 x  x 2  x  2 x 2  x3
 1  3x  3x 2  x 3
1  x 4  1  x 1  3x  3x 2  x 3 
 1  3x  3x 2  x 3  x  3x 2  3x 3  x 4
 1  4 x  6 x 2  4 x3  x 4

8. Blaise Pascal saw a pattern which we now know as Pascal’s Triangle

9. Blaise Pascal saw a pattern which we now know as Pascal’s Triangle
1

10. Blaise Pascal saw a pattern which we now know as Pascal’s Triangle
1
1 1

11. Blaise Pascal saw a pattern which we now know as Pascal’s Triangle
1
1 1
1 2 1

12. Blaise Pascal saw a pattern which we now know as Pascal’s Triangle
1
1 1
1 2 1
1 3 3 1

13. Blaise Pascal saw a pattern which we now know as Pascal’s Triangle
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1

14. Blaise Pascal saw a pattern which we now know as Pascal’s Triangle
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1

15. Blaise Pascal saw a pattern which we now know as Pascal’s Triangle
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1

16. Blaise Pascal saw a pattern which we now know as Pascal’s Triangle
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1

17. Blaise Pascal saw a pattern which we now know as Pascal’s Triangle
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1

18. Blaise Pascal saw a pattern which we now know as Pascal’s Triangle
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1

19. Blaise Pascal saw a pattern which we now know as Pascal’s Triangle
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 28 856 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
1 10 45 120 210 252 210 120 45 10 1

20. 7
  2x 
e.g .i 1 
 3

21. 7
  2x 
e.g .i 1 
 3
2 3 4 5
 17  71    211    351    351    211  
6 2x 5 2x 4 2x 3 2x 2 2x
         
 3  3  3  3  3
6 7
 2x    2x 
 71   
 3  3

22. 7
  2x 
e.g .i 1 
 3
2 3 4 5
 17  71    211    351    351    211  
6 2x 5 2x 4 2x 3 2x 2 2x
         
 3  3  3  3  3
6 7
 2x    2x 
 71   
 3  3
14 x 84 x 2 280 x 3 560 x 4 672 x 5 448 x 6 128 x 7
 1      
3 9 27 81 243 729 2187

23. 7
  2x 
e.g .i 1 
 3
2 3 4 5
 17  71    211    351    351    211  
6 2x 5 2x 4 2x 3 2x 2 2x
         
 3  3  3  3  3
6 7
 2x    2x 
 71   
 3  3
14 x 84 x 2 280 x 3 560 x 4 672 x 5 448 x 6 128 x 7
 1      
3 9 27 81 243 729 2187
ii  Use the expansion of 1  x 10 to find the value of 0.99810 to 8 dps

24. 7
1  2 x 
e.g .i  
 3
2 3 4 5
 17  71    211    351    351    211  
6 2x 5 2x 4 2x 3 2x 2 2x
         
 3  3  3  3  3
6 7
 2x    2x 
 71   
 3  3
14 x 84 x 2 280 x 3 560 x 4 672 x 5 448 x 6 128 x 7
 1      
3 9 27 81 243 729 2187
ii  Use the expansion of 1  x 10 to find the value of 0.99810 to 8 dps
1  x 10  1  10 x  45 x 2  120 x 3  210 x 4  252 x 5  210 x 6  120 x 7  45 x8
 10 x 9  x10

25. 7
1  2 x 
e.g .i  
 3
2 3 4 5
 17  71    211    351    351    211  
6 2x 5 2x 4 2x 3 2x 2 2x
         
 3  3  3  3  3
6 7
 2x    2x 
 71   
 3  3
14 x 84 x 2 280 x 3 560 x 4 672 x 5 448 x 6 128 x 7
 1      
3 9 27 81 243 729 2187
ii  Use the expansion of 1  x 10 to find the value of 0.99810 to 8 dps
1  x 10  1  10 x  45 x 2  120 x 3  210 x 4  252 x 5  210 x 6  120 x 7  45 x8
 10 x 9  x10
0.99810  1  100.002  450.0022  1200.0023

26. 7
1  2 x 
e.g .i  
 3
2 3 4 5
 17  71    211    351    351    211  
6 2x 5 2x 4 2x 3 2x 2 2x
         
 3  3  3  3  3
6 7
 2x    2x 
 71   
 3  3
14 x 84 x 2 280 x 3 560 x 4 672 x 5 448 x 6 128 x 7
 1      
3 9 27 81 243 729 2187
ii  Use the expansion of 1  x 10 to find the value of 0.99810 to 8 dps
1  x 10  1  10 x  45 x 2  120 x 3  210 x 4  252 x 5  210 x 6  120 x 7  45 x8
 10 x 9  x10
0.998  1  100.002  450.002  1200.002
10 2 3
 0.98017904

27. iii  Find the coefficient of x 2 in 2  3x 4  5 x 4

28. iii  Find the coefficient of x 2 in 2  3x 4  5 x 4
2  3x 4  5 x 4
 2  3 x 44  443 5x   642 5x 2  445x 3  5x 4 

29. iii  Find the coefficient of x 2 in 2  3x 4  5 x 4
2  3x 4  5 x 4
 2  3 x 44  443 5x   642 5x 2  445x 3  5x 4 

30. iii  Find the coefficient of x 2 in 2  3x 4  5 x 4
2  3x 4  5 x 4
 2  3 x 44  443 5x   642 5x 2  445x 3  5x 4 

31. iii  Find the coefficient of x 2 in 2  3x 4  5 x 4
2  3x 4  5 x 4
 2  3 x 44  443 5x   642 5x 2  445x 3  5x 4 
 coefficient of x 2  26 4  5  34 4  5
2 2 3

32. iii  Find the coefficient of x 2 in 2  3x 4  5 x 4
2  3x 4  5 x 4
 2  3 x 44  443 5x   642 5x 2  445x 3  5x 4 
 coefficient of x 2  26 4  5  34 4  5
2 2 3
 4800  3840
 960

33. iii  Find the coefficient of x 2 in 2  3x 4  5 x 4
2  3x 4  5 x 4
 2  3 x 44  443 5x   642 5x 2  445x 3  5x 4 
 coefficient of x 2  26 4  5  34 4  5
2 2 3
 4800  3840
 960
Exercise 5A; 2ace etc, 4, 6, 7, 9ad, 12b, 13ac, 14ace, 16a, 22, 23