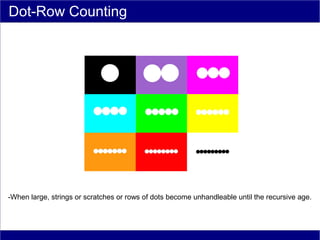
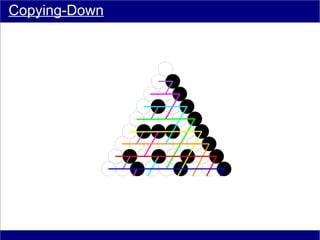
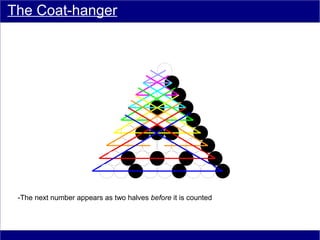
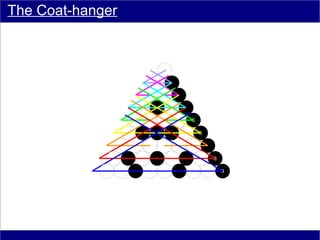
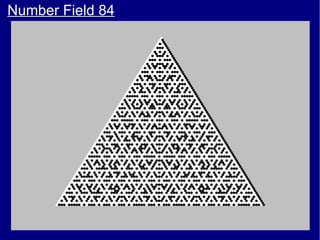
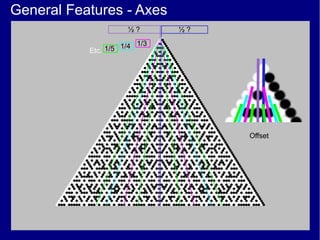
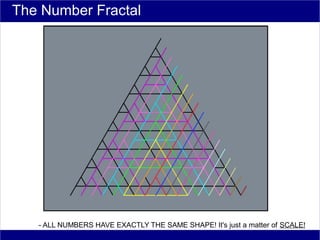
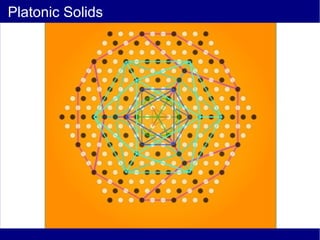
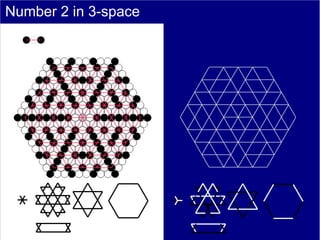
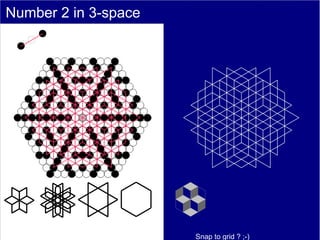
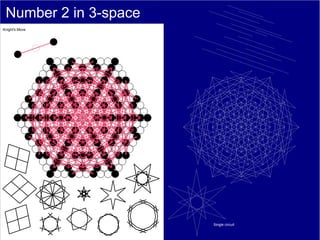
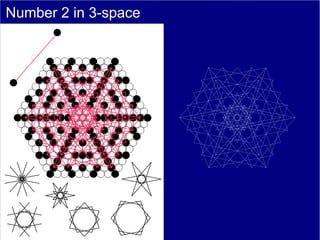
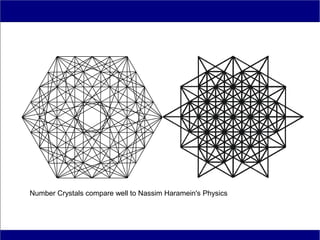
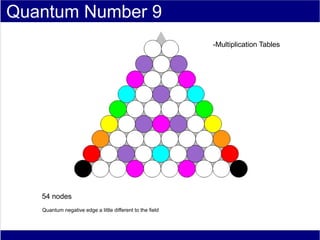
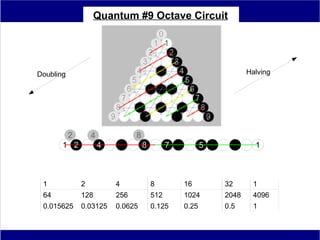
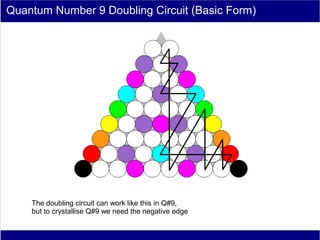
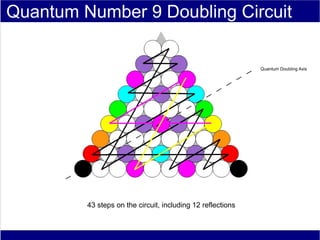
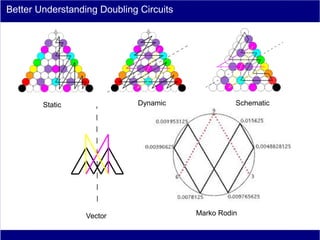
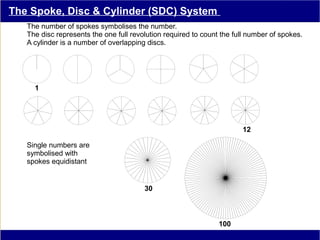
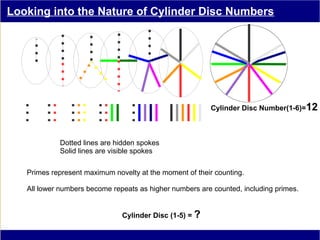
This document discusses various methods of counting and deriving number fields. It begins by describing dot-row counting, pyramid counting, and triangular numbers. It then discusses different methods for deriving the number field, including the copy-down method, coat-hanger method, and algebraic method. The document goes on to describe features of the number field such as conservation of information, negative edges, and applications. It concludes that correct counting involves distinguishing novel from repeated information, and basic exploration of these concepts yields insights into the nature of number fields.

1. 7 March 2013

2. This Presentation:
Counting Mapping Imaginary Space
- Dot-row Counting The Platonic Solids
- Pyramid Counting Number Crystals
- Triangular Numbers Quantum Number
Derivation of the Number Field Marko Rodin's Vortex Math
-the Copy-Down Method
-the Coat-hanger Method The Spoke, Cylinder, Disc System of Counting
-the Algebraic Method The Three Number Highest Dies Game
Number Field 84 (Raw)
Novelty
Numbers as Strings
General Features of the Number Field
-the Habit of Conservation of Information
-Introducing the Negative Edge (necessity?)
Number Field 84 (Complete?)
What is the Number Field?
What are the Applications?

3. Counting
What is counting?
My definition is: The process of symbolising number.
Remember, numbers are purely mental objects, whilst symbols can be both physical
and mental objects. Put together this means:
The accuracy of our number symbols determines our understanding of number.
These are not numbers:
3
1
2
...but they are number symbols!

4. Dot-Row Counting
-When large, strings or scratches or rows of dots become unhandleable until the recursive age.

5. Pyramid Counting
- Close-Packed Circles
- Habit of the Conservation of Information
- Axonometric projection
- Capacity for a new dimension: depth - Pascals triangle etc

6. Triangular Numbers
The First 100
9
84

7. Derivation of the Number Field:
-Copying-Down
-Coat-hanger
-Algebraic?
-Axial?

8. Copying-Down

9. Copying-Down
1
2
3
Choice point
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

10. The Coat-hanger
-The next number appears as two halves before it is counted

11. The Coat-hanger
5
6
8
9

12. The Algebraic Derivation
X X>Y? Then let X=X-Y
Y Y>X? Then let X=Y and Y=X
1
1
Results:
1/1 = +ve (white, one, novel) 1
2
2
2
Other = -ve (black, zero, repeat) 1 2 3
3 3 3
1 2 3 4
4 4 4 4
1 2 3 4 5
5 5 5 5 5
1 2 3 4 5 6
6 6 6 6 6 6
1 2 3 4 5 6 7
7 7 7 7 7 7 7
1 2 3 4 5 6 7 8
8 8 8 8 8 8 8 8
1 2 3 4 5 6 7 8 9
9 9 9 9 9 9 9 9 9
- 3 Number Highest Dies method
Take any two different numbers,
Create a third using the difference,
Delete the highest number of the three,
Begin again.
1 / 1 = Novel (choice point)

13. Number Field 84

14. Novelty
Disc Cylinder-Disc Previous NOVELTY
Number Number Cylinder-Disc FACTOR (X)
(A) Number
(B) X =A-B
1 1 0 1
2 2 1 1
3 4 2 2
4 6 4 2
5 10 6 4
6 12 10 2

15. Number as Strings / Beats / Sequences / Vectors
1
Binary 2,4,8,16,32 etc.
3
Primes
6
9
10
12
14
15
18
20

16. General Features of the Number Field The Habit of the
Conservation of Information
- Black cells are patterns of factors
- White cells are novel The Positive Edge, not reflected on the opposite edge
The same number can be
found at various angles
15
Primary Axes?
Repeated Single Number count
Single Numbers (1 out of phase?)
Single Number count
85/2
Bottom edge is infinite as long as 'counting' continues

17. General Features - Axes
½? ½?
1/3
Etc. 1/5 1/4
Offset

18. The Negative Edge
e
dgE
g.
Ne

19. What is the Number Field? Applications?
-Universal Imaginary Shape?
-the same in all cultures, all places,, all
times?
-the 'hard-copy' or static version of the
process
of counting?
-a teaching aid ?
-A FRACTAL?
- COUNTING

20. The Number Fractal
- ALL NUMBERS HAVE EXACTLY THE SAME SHAPE! It's just a matter of SCALE!

21. Mapping Imaginary Space Using Number Crystals
- zero point in grey

22. Platonic Solids

23. Number 2 in 3-space

24. Number 2 in 3-space
Snap to grid ? ;-)

25. Number 2 in 3-space
Knight's Move
Single circuit

26. Number 2 in 3-space

27. Number Crystals compare well to Nassim Haramein's Physics

28. Quantum Number 9
-Multiplication Tables
54 nodes
Quantum negative edge a little different to the field

29. Quantum #9 Octave Circuit
Doubling Halving
2 4 8
1 2 4 8 7 5 1
1 2 4 8 16 32 1
64 128 256 512 1024 2048 4096
0.015625 0.03125 0.0625 0.125 0.25 0.5 1

30. Quantum Number 9 Doubling Circuit (Basic Form)
The doubling circuit can work like this in Q#9,
but to crystallise Q#9 we need the negative edge

31. Quantum Number 9 Doubling Circuit
Quantum Doubling Axis
43 steps on the circuit, including 12 reflections

32. Quantum Number Crystal 9

33. Better Understanding Doubling Circuits

34. Better Understanding Doubling Circuits
Static Dynamic Schematic
Vector Marko Rodin

35. The Spoke, Disc & Cylinder (SDC) System
The number of spokes symbolises the number.
The disc represents the one full revolution required to count the full number of spokes.
A cylinder is a number of overlapping discs.
1
12
Single numbers are
symbolised with
spokes equidistant
30
100

36. Cylinder Discs
Overlapping discs produce composite discs, or Cylinder Discs
Discs 1 and 2 overlapped produce a
Cylinder Disc identical to disc 2.
Discs 1,2, and 3 produce this Cylinder Disc(1-3)
Cylinder Disc (1-4)
Cylinder Disc (1-5)
Cylinder Disc (1-6)

37. Cylinder Disc Numbers
1
12 2
11 3
10 4 Cylinder Disc (1-6)
9 5
8 6
7
1 + 2 + 3 + 4 + 5 + 6 = 21 1 x 2 x 3 x 4 x 5 x 6 = 720
And yet the Cylinder Disc (1-6) has a count of 12
I don't know what to call these Cylinder Disc numbers,
but they are not sums (additions) or factorials (multiplications).

38. Novelty Factor X
Disc Cylinder-Disc Previous NOVELTY
Number Number Cylinder-Disc FACTOR (X)
(A) Number
(B) X =A-B
1 1 0 1
2 2 1 1
3 4 2 2
4 6 4 2
5 10 6 4
6 12 10 2

39. Primality Test
n A B X n-X Prime?
1 1 0 1 0 no
Let Disc n = a test number
2 2 1 1 1 yes
counted using SDC
3 4 2 2 1 yes
4 6 4 2 2 no
If n - X = ? ... 5 10 6 4 1 yes
Disc CD 6 12 10 2 4 no
(n) (A)
7 18 12 6 1 yes
Cylinder Disc A 8 22 18 4 4 no
Cylinder A (1 to n) X = CD(A - B)
9 28 22 6 3 no
10 32 28 4 6 no
Disc CD
(n-1) (B) If n - X = 1 11 42 32 10 1 yes
then n is prime 12 46 42 4 8 no
Cylinder B (1 to n-1) Cylinder Disc B 13 58 46 12 1 yes
14 64 58 6 8 no
15 72 64 8 7 no
16 80 72 8 8 no
17 96 80 16 1 yes
18 102 96 6 12 no
19 120 102 18 1 yes
20 128 120 8 12 no
21 140 128 12 9 no
22 150 140 10 12 no
23 172 150 22 1 yes

40. Looking into the Nature of Cylinder Disc Numbers
Cylinder Disc Number(1-6)=12
Dotted lines are hidden spokes
Solid lines are visible spokes
Primes represent maximum novelty at the moment of their counting.
All lower numbers become repeats as higher numbers are counted, including primes.
Cylinder Disc (1-5) = ?

41. Conclusions
1. There seems to be such a thing (object) as the Number Field
2. This object evolves from counting correctly
3. Counting Correctly will involve information about which parts of number are novel
and which are repeated
4. Basic Exploration of the above concepts yields...
END