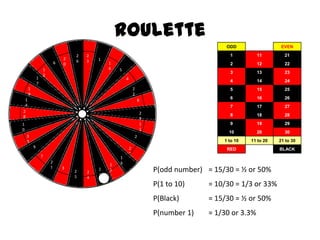
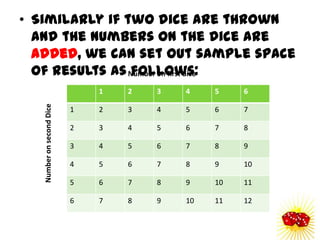
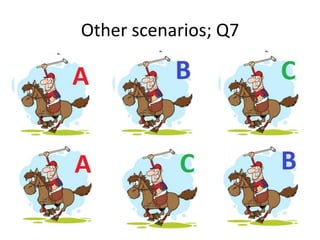
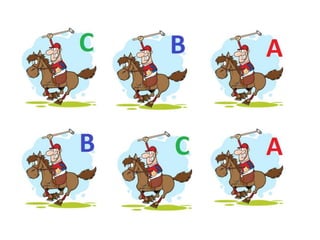
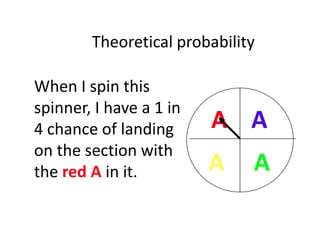
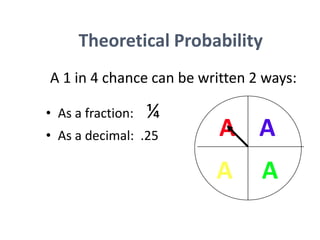
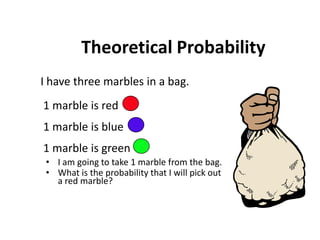
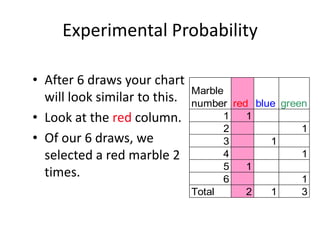
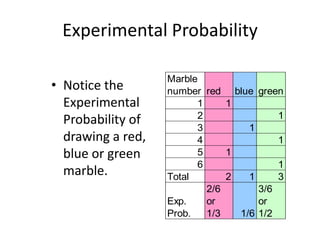
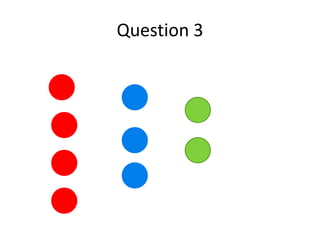
The document discusses probability and chance. It defines probability as a number between 0 and 1 that indicates how likely something is to occur. It distinguishes between theoretical and experimental probability. Theoretical probability can be calculated without experiments, while experimental probability is determined by performing repeated trials of an experiment and observing outcomes. Examples are provided to illustrate calculating probabilities of events using fractions, decimals, sample spaces, and tally charts.