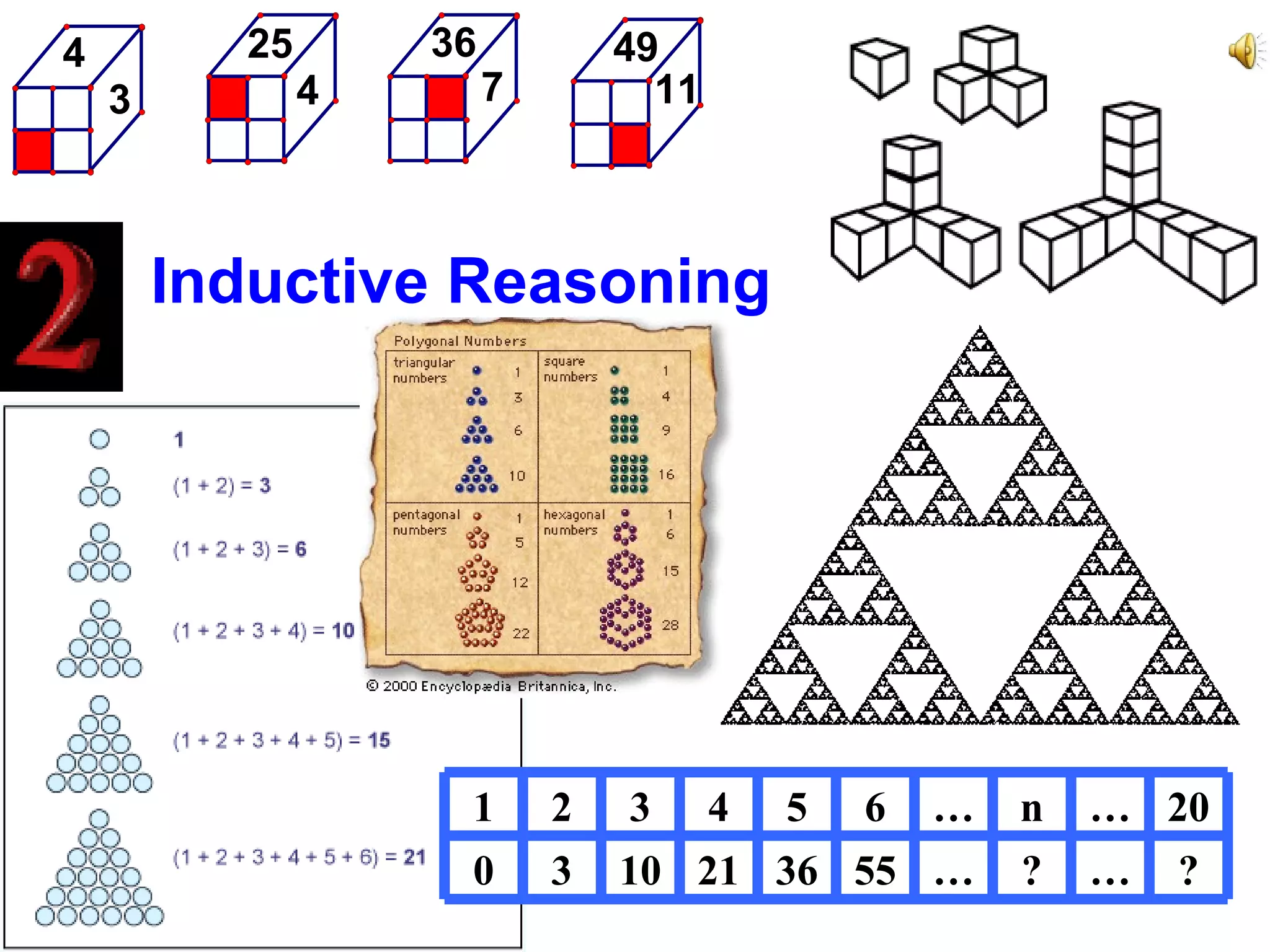
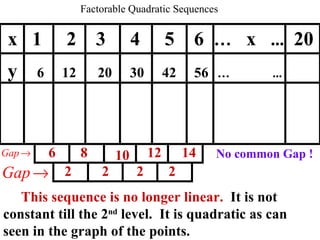
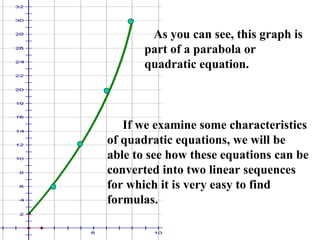
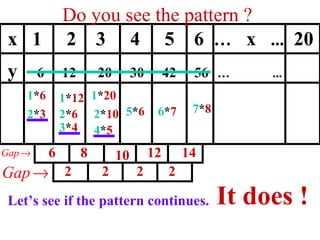
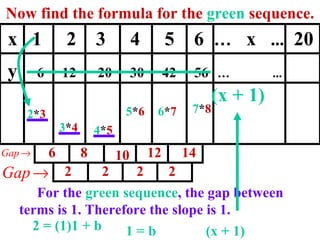
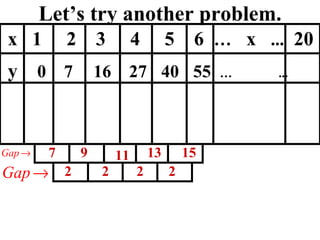
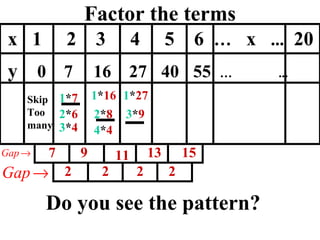
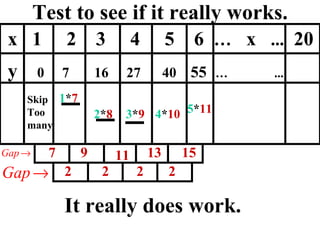
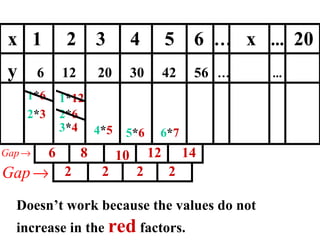
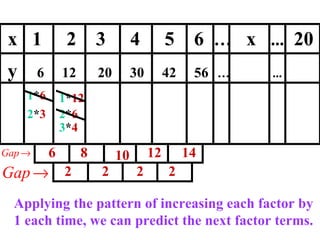
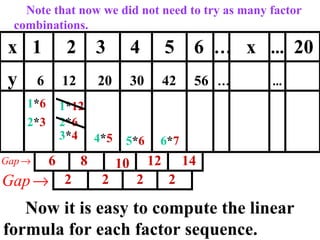
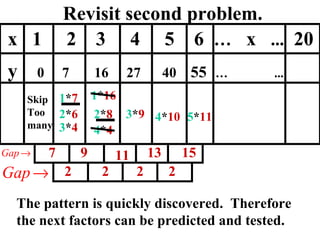
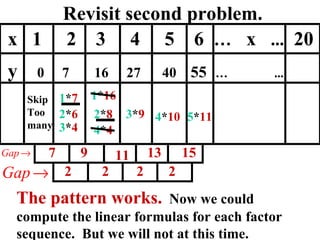
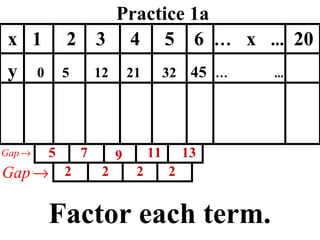
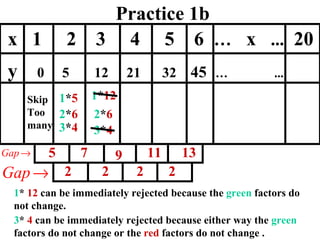
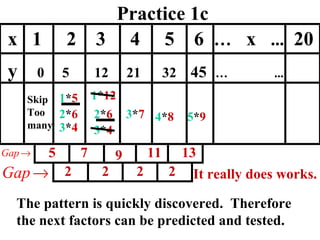
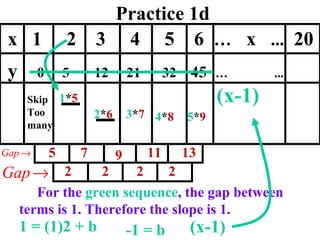
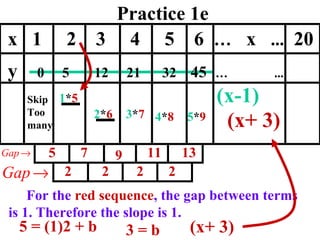
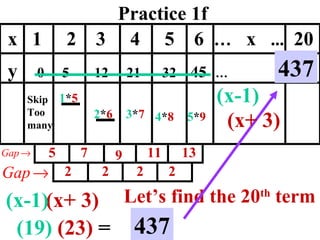
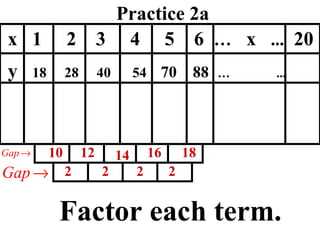
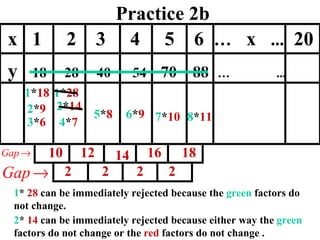
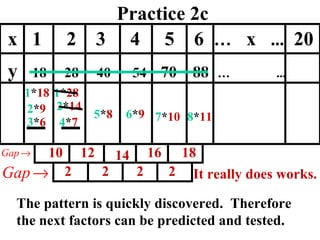
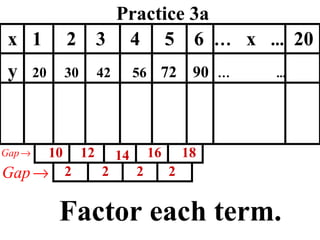
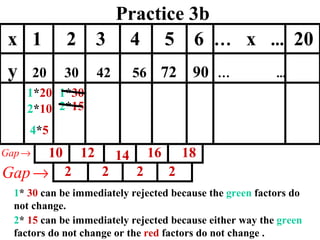
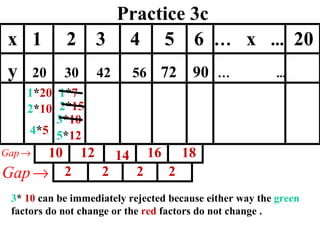
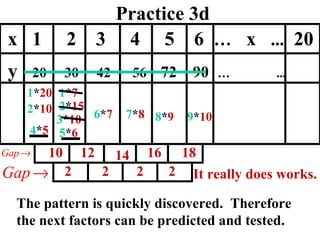
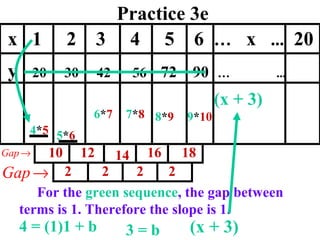
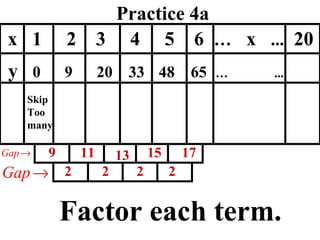
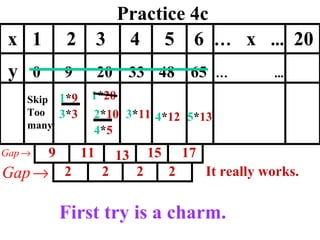
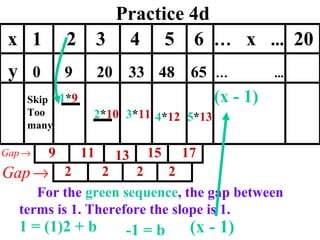
The document discusses factoring quadratic sequences into linear factors. It provides examples of factoring sequences into two linear sequences and deriving the formulas for each. Elimination strategies are discussed to reduce the number of attempts needed to find the correct factors, by rejecting factors that don't produce continuously increasing or decreasing sequences. Practice problems are included to have the reader practice applying the techniques.

1. Inductive Reasoning 1 2 3 4 5 6 … n … 20 0 3 10 21 36 55 … ? … ?

2. Quadratic Sequences Terms: 4, 25, 36, 49, 64 … 3, 24, 35, 48, 63 … 6, 12, 20, 30, 42 …

3. Factorable Quadratic Sequences x 1 2 3 4 5 6 … x ... 20 y 6 12 20 30 42 56 … ... This sequence is no longer linear. It is not constant till the 2 nd level. It is quadratic as can seen in the graph of the points. 6 8 10 12 14 2 2 2 2 No common Gap !

4. As you can see, this graph is part of a parabola or quadratic equation. If we examine some characteristics of quadratic equations, we will be able to see how these equations can be converted into two linear sequences for which it is very easy to find formulas.

5. Solving Quadratic Equations Set = to 0, then factor. The two factors are in y = mx + b form. If we factor the terms into linear sequences, then each factor can be easily converted into an algebraic expression in the form or mx + b . Wait !

6. Break terms into factors 1 * 6 2 * 3 1 * 12 2 * 6 3 * 4 4 * 5 2 * 10 1 * 20 x 1 2 3 4 5 6 … x ... 20 y 6 12 20 30 42 56 … ... Only certain combination will create two linear sequences. Our difficulty is determining which factors will create the sequences. 6 8 10 12 14 2 2 2 2

7. Do you see the pattern ? 1 * 6 2 * 3 1 * 12 2 * 6 3 * 4 4 * 5 2 * 10 1 * 20 5 * 6 6 * 7 x 1 2 3 4 5 6 … x ... 20 y 6 12 20 30 42 56 … ... Let’s see if the pattern continues. 6 8 10 12 14 2 2 2 2 7 * 8 It does !

8. Now find the formula for the green sequence. 2 * 3 3 * 4 4 * 5 5 * 6 6 * 7 x 1 2 3 4 5 6 … x ... 20 y 6 12 20 30 42 56 … ... For the green sequence , the gap between terms is 1. Therefore the slope is 1. 6 8 10 12 14 2 2 2 2 7 * 8 2 = (1)1 + b 1 = b (x + 1) (x + 1)

9. Now find the formula for the red sequence. 2 * 3 3 * 4 4 * 5 5 * 6 6 * 7 x 1 2 3 4 5 6 … x ... 20 y 6 12 20 30 42 56 … ... For the red sequence , the gap between terms is also 1. Therefore the slope is 1. 6 8 10 12 14 2 2 2 2 7 * 8 3 = (1)1 + b 2 = b (x + 2) (x + 1) (x + 2)

10. Now let’s find the 20 th term. 2 * 3 3 * 4 4 * 5 5 * 6 6 * 7 x 1 2 3 4 5 6 … x ... 20 y 6 12 20 30 42 56 … ... Substitute 20 for x. 6 8 10 12 14 2 2 2 2 7 * 8 (x + 1) (x + 2) (x + 2) (x + 1) (21) (22) = 462

11. Let’s try another problem. x 1 2 3 4 5 6 … x ... 20 y 0 7 16 27 40 55 … ... 7 9 11 13 15 2 2 2 2

12. Factor the terms 1 * 7 2 * 6 3 * 4 4 * 4 2 * 8 1 * 16 x 1 2 3 4 5 6 … x ... 20 y 0 7 16 27 40 55 … ... 7 9 11 13 15 2 2 2 2 3 * 9 1 * 27 Do you see the pattern? Skip Too many

13. Test to see if it really works. 1 * 7 2 * 8 x 1 2 3 4 5 6 … x ... 20 y 0 7 16 27 40 55 … ... 7 9 11 13 15 2 2 2 2 3 * 9 It really does work. Skip Too many 4 * 10 5 * 11

14. Now find the formula for the green sequence. 1 * 7 2 * 8 x 1 2 3 4 5 6 … x ... 20 y 0 7 16 27 40 72 … ... 7 9 11 13 15 2 2 2 2 3 * 9 Skip Too many 4 * 10 5 * 11 For the green sequence , the gap between terms is 1. Therefore the slope is 1. 1 = (1)2 + b -1 = b (x-1) (x-1)

15. Now find the formula for the red sequence. 1 * 7 2 * 8 x 1 2 3 4 5 6 … x ... 20 y 0 7 16 27 40 72 … ... 7 9 11 13 15 2 2 2 2 3 * 9 Skip Too many 4 * 10 5 * 11 For the red sequence , the gap between terms is 1. Therefore the slope is 1. 7 = (1)2 + b 5 = b (x + 5) (x-1) (x + 5)

16. Let’s find the 20 th term 1 * 7 2 * 8 x 1 2 3 4 5 6 … x ... 20 y 0 7 16 27 40 72 … ... 7 9 11 13 15 2 2 2 2 3 * 9 Skip Too many 4 * 10 5 * 11 (x-1) (x + 5) 475 (x-1) (x + 5) (19) (25) =

17. Elimination Strategies All linear sequence either constantly increase or constantly decrease. Therefore if the sequence doesn’t continually increase or decrease, the factors can be rejected. Knowing this will increase the speed of finding the correct set of factors..

18. Revisit first problem. 1 * 6 2 * 3 1 * 12 2 * 6 3 * 4 x 1 2 3 4 5 6 … x ... 20 y 6 12 20 30 42 56 … ... 6 8 10 12 14 2 2 2 2 1 * 12 can be immediately rejected because the green factors do not change. 2 * 6 can be immediately rejected because either way the green factors do not change or the red factors do not change .

19. 2 * 3 1 * 12 2 * 6 3 * 4 x 1 2 3 4 5 6 … x ... 20 y 6 12 20 30 42 56 … ... 6 8 10 12 14 2 2 2 2 4 * 5 5 * 6 6 * 7 1 * 6 Doesn’t work because the values do not increase in the red factors.

20. 2 * 3 1 * 12 2 * 6 3 * 4 x 1 2 3 4 5 6 … x ... 20 y 6 12 20 30 42 56 … ... 6 8 10 12 14 2 2 2 2 Applying the pattern of increasing each factor by 1 each time, we can predict the next factor terms. 1 * 6

21. 1 * 6 2 * 3 1 * 12 2 * 6 3 * 4 x 1 2 3 4 5 6 … x ... 20 y 6 12 20 30 42 56 … ... 6 8 10 12 14 2 2 2 2 4 * 5 5 * 6 6 * 7 Note that now we did not need to try as many factor combinations. Now it is easy to compute the linear formula for each factor sequence.

22. By using the concept that the linear factors need to increase or decrease every time, the number of trials to find the correct sequence of factors is greatly reduced.

23. Revisit second problem. 1 * 7 2 * 6 3 * 4 4 * 4 2 * 8 1 * 16 x 1 2 3 4 5 6 … x ... 20 y 0 7 16 27 40 72 … ... 7 9 11 13 15 2 2 2 2 Skip Too many 1 * 16 can be immediately rejected because the green factors do not change. 4 * 4 can be immediately rejected because either way the green factors do not change or the red factors do not change properly.

24. Revisit second problem. 1 * 7 2 * 6 3 * 4 4 * 4 2 * 8 1 * 16 x 1 2 3 4 5 6 … x ... 20 y 0 7 16 27 40 55 … ... 7 9 11 13 15 2 2 2 2 3 * 9 Skip Too many The pattern is quickly discovered. Therefore the next factors can be predicted and tested. 4 * 10 5 * 11

25. Revisit second problem. 1 * 7 2 * 6 3 * 4 4 * 4 2 * 8 1 * 16 x 1 2 3 4 5 6 … x ... 20 y 0 7 16 27 40 55 … ... 7 9 11 13 15 2 2 2 2 3 * 9 Skip Too many The pattern works. Now we could compute the linear formulas for each factor sequence. But we will not at this time. 4 * 10 5 * 11

26. Now we need to practice. Let’s begin.

27. Practice 1a x 1 2 3 4 5 6 … x ... 20 y 0 5 12 21 32 45 … ... 5 7 9 11 13 2 2 2 2 Factor each term.

28. Practice 1b 1 * 5 2 * 6 3 * 4 3 * 4 2 * 6 1 * 12 x 1 2 3 4 5 6 … x ... 20 y 0 5 12 21 32 45 … ... 2 2 2 2 Skip Too many 1 * 12 can be immediately rejected because the green factors do not change. 3 * 4 can be immediately rejected because either way the green factors do not change or the red factors do not change . 5 7 9 11 13

29. Practice 1c 1 * 5 2 * 6 3 * 4 3 * 4 2 * 6 1 * 12 x 1 2 3 4 5 6 … x ... 20 y 0 5 12 21 32 45 … ... 2 2 2 2 3 * 7 Skip Too many 4 * 8 5 * 9 The pattern is quickly discovered. Therefore the next factors can be predicted and tested. It really does works. 5 7 9 11 13

30. Practice 1d 1 * 5 2 * 6 x 1 2 3 4 5 6 … x ... 20 y 0 5 12 21 32 45 … ... 2 2 2 2 3 * 7 Skip Too many 4 * 8 5 * 9 For the green sequence , the gap between terms is 1. Therefore the slope is 1. 1 = (1)2 + b -1 = b (x-1) (x-1) 5 7 9 11 13

31. Practice 1e 1 * 5 2 * 6 x 1 2 3 4 5 6 … x ... 20 y 0 5 12 21 32 45 … ... 2 2 2 2 3 * 7 Skip Too many 4 * 8 5 * 9 For the red sequence , the gap between terms is 1. Therefore the slope is 1. 5 = (1)2 + b 3 = b (x+ 3) (x-1) (x+ 3) 5 7 9 11 13

32. Practice 1f 1 * 5 2 * 6 x 1 2 3 4 5 6 … x ... 20 y 0 5 12 21 32 45 … ... 2 2 2 2 3 * 7 Skip Too many 4 * 8 5 * 9 (x-1) (x+ 3) Let’s find the 20 th term (x-1) (19) (23) = 437 437 (x+ 3) 5 7 9 11 13

33. Practice 2a x 1 2 3 4 5 6 … x ... 20 y 18 28 40 54 70 88 … ... 10 12 14 16 18 2 2 2 2 Factor each term.

34. Practice 2b 1 * 28 1 * 18 2 * 14 4 * 7 5 * 8 x 1 2 3 4 5 6 … x ... 20 y 18 28 40 54 70 88 … ... 2 2 2 2 6 * 9 7 * 10 8 * 11 2 * 9 3 * 6 1 * 28 can be immediately rejected because the green factors do not change. 2 * 14 can be immediately rejected because either way the green factors do not change or the red factors do not change . 10 12 14 16 18

35. Practice 2c 1 * 28 4 * 7 3 * 6 1 * 18 2 * 14 5 * 8 x 1 2 3 4 5 6 … x ... 20 y 18 28 40 54 70 88 … ... 2 2 2 2 6 * 9 7 * 10 8 * 11 2 * 9 The pattern is quickly discovered. Therefore the next factors can be predicted and tested. It really does works. 10 12 14 16 18

36. Practice 2d 4 * 7 5 * 8 x 1 2 3 4 5 6 … x ... 20 y 18 28 40 54 70 88 … ... 2 2 2 2 6 * 9 7 * 10 8 * 11 3 * 6 For the green sequence , the gap between terms is 1. Therefore the slope is 1. 3 = (1)1 + b 2 = b (x + 2) (x + 2) 10 12 14 16 18

37. Practice 2e 4 * 7 5 * 8 x 1 2 3 4 5 6 … x ... 20 y 18 28 40 54 70 88 … ... 2 2 2 2 6 * 9 7 * 10 8 * 11 3 * 6 For the red sequence , the gap between terms is 1. Therefore the slope is 1. 6 = (1)1 + b 5 = b (x + 5) (x + 2) (x + 5) 10 12 14 16 18

38. Practice 2f 4 * 7 5 * 8 x 1 2 3 4 5 6 … x ... 20 y 18 28 40 54 70 88 … ... 2 2 2 2 6 * 9 7 * 10 8 * 11 3 * 6 (x+2) (x + 5) Let’s find the 20 th term (x + 5) (x+2) (22) (25) = 550 550 10 12 14 16 18

39. Practice 3a x 1 2 3 4 5 6 … x ... 20 y 20 30 42 56 72 90 … ... 2 2 2 2 Factor each term. 10 12 14 16 18

40. Practice 3b 1 * 30 2 * 15 x 1 2 3 4 5 6 … x ... 20 y 20 30 42 56 72 90 … ... 2 2 2 2 1 * 20 2 * 10 4 * 5 1 * 30 can be immediately rejected because the green factors do not change. 2 * 15 can be immediately rejected because either way the green factors do not change or the red factors do not change . 10 12 14 16 18

41. Practice 3c 3 * 10 1 * 7 2 * 15 x 1 2 3 4 5 6 … x ... 20 y 20 30 42 56 72 90 … ... 2 2 2 2 1 * 20 2 * 10 4 * 5 3 * 10 can be immediately rejected because either way the green factors do not change or the red factors do not change . 5 * 12 10 12 14 16 18

42. Practice 3d 5 * 6 4 * 5 1 * 7 2 * 15 3 * 10 6 * 7 x 1 2 3 4 5 6 … x ... 20 y 20 30 42 56 72 90 … ... 2 2 2 2 7 * 8 8 * 9 9 * 10 1 * 20 2 * 10 The pattern is quickly discovered. Therefore the next factors can be predicted and tested. It really does works. 10 12 14 16 18

43. Practice 3e 6 * 7 x 1 2 3 4 5 6 … x ... 20 y 20 30 42 56 72 90 … ... 2 2 2 2 7 * 8 8 * 9 9 * 10 4 * 5 5 * 6 For the green sequence , the gap between terms is 1. Therefore the slope is 1. 4 = (1)1 + b 3 = b (x + 3) (x + 3) 10 12 14 16 18

44. Practice 3f 6 * 7 x 1 2 3 4 5 6 … x ... 20 y 20 30 42 56 72 90 … ... 2 2 2 2 7 * 8 8 * 9 9 * 10 4 * 5 5 * 6 (x + 3) For the red sequence , the gap between terms is 1. Therefore the slope is 1. 5 = (1)1 + b 4 = b (x + 4) (x + 4) 10 12 14 16 18

45. Practice 3g 6 * 7 x 1 2 3 4 5 6 … x ... 20 y 20 30 42 56 72 90 … ... 2 2 2 2 7 * 8 8 * 9 9 * 10 4 * 5 5 * 6 (x + 3) Let’s find the 20 th term (x + 4) (x + 3) (x + 4) (23) (24) = 552 552 10 12 14 16 18

46. Practice 4a x 1 2 3 4 5 6 … x ... 20 y 0 9 20 33 48 65 … ... 9 11 13 15 17 2 2 2 2 Skip Too many Factor each term.

47. Practice 4b 1 * 9 3 * 3 4 * 5 2 * 10 1 * 20 x 1 2 3 4 5 6 … x ... 20 y 0 9 20 33 48 65 … ... 2 2 2 2 Skip Too many 1 * 20 can be immediately rejected because the green factors do not change. 9 11 13 15 17 Let’s try the pattern of 1*9 and 2*10.

48. Practice 4c 1 * 9 3 * 3 4 * 5 2 * 10 1 * 20 x 1 2 3 4 5 6 … x ... 20 y 0 9 20 33 48 65 … ... 2 2 2 2 3 * 11 Skip Too many 4 * 12 5 * 13 First try is a charm. It really works. 9 11 13 15 17

49. Practice 4d x 1 2 3 4 5 6 … x ... 20 y 0 9 20 33 48 65 … ... 2 2 2 2 Skip Too many For the green sequence , the gap between terms is 1. Therefore the slope is 1. 1 = (1)2 + b -1 = b (x - 1) 9 11 13 15 17 1 * 9 2 * 10 3 * 11 4 * 12 5 * 13 (x - 1)

50. Practice 4e 1 * 9 2 * 10 x 1 2 3 4 5 6 … x ... 20 y 0 9 20 33 48 65 … ... 2 2 2 2 Skip Too many For the red sequence , the gap between terms is 1. Therefore the slope is 1. 9 = (1)2 + b 7 = b (x + 7) 9 11 13 15 17 3 * 11 4 * 12 5 * 13 (x - 1) (x + 7)

51. Practice 4f 1 * 9 2 * 10 x 1 2 3 4 5 6 … x ... 20 y 0 9 20 33 48 65 … ... 2 2 2 2 Skip Too many Let’s find the 20 th term 9 11 13 15 17 3 * 11 4 * 12 5 * 13 (x - 1) (x + 7) (x + 7) (x - 1) (19) (27) = 513 513

52. Summary When the gap between terms of sequences are constant on the second level, the sequence is quadratic or second degree. The rule for each term is created by the factors of each term which create their own linear sequence. The quadratic sequence is treated as the product of 2 linear sequences.

53. Time can be saved by assuming a pattern exists in the first two columns of factors, then seeing if the terms can correctly predict the following terms. Also, time can be saved by rejecting terms that do not increase or decrease. These problems require a lot of practice.

54. C’est fini. Good day and good luck. A Senior Citizen Production That’s all folks.

55. C’est fini. Good day and good luck.