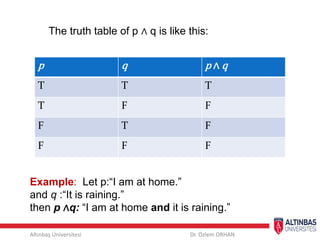
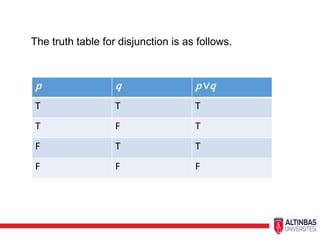
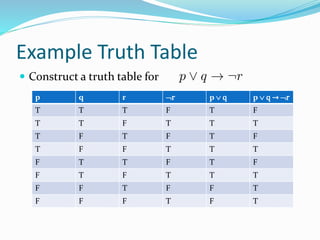
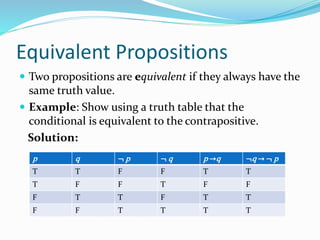
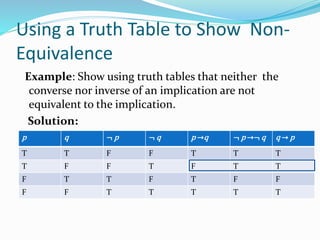
This document provides an introduction to propositional logic and logical connectives. It defines propositions, truth values, and logical connectives such as negation, conjunction, disjunction, implication, biconditional, and how to represent them using truth tables. Examples are given for each logical connective. The document also discusses compound statements, equivalent statements, and precedence of logical operators.

1. DISCRETE
MATHEMATICS
MAT 211

2. DISCRETE
MATHEMATICS
Propositional
Logic
ALTINBAŞ ÜNİVERSİTESİ ÖZLEM ORHAN
DISCRETE MATHEMATICS
Week I

3. Asst. Prof. Özlem Orhan
orhanozlem@itu.edu.tr

4. Summary
 Propositions
 Connectives
 Negation
 Conjunction
 Disjunction
 Implication; contrapositive, inverse, converse
 Biconditional
 Truth Tables

5. Altınbaş Üniversitesi Dr. Özlem ORHAN
Propositions
Examples of propositions:
a) Istanbul is the capital of Turkey.
b) Ankara is the capital of Canada.
c) 1 + 0 = 1
d) 0 + 0 = 2
e) The square of 5 is 15.
f) 5<4.
A proposition (or a statement) is a declarative sentence that
is either true or false.

6. Examples that are not propositions:
a) Sit down!
b) What time is it?
c) x + 1 = 2
d) x + y = z
e) What are you doing?
f) Do your homework
g) May God bless you!
Altınbaş Üniversitesi Dr. Özlem ORHAN

7. Altınbaş Üniversitesi Dr. Özlem ORHAN
Compound statements:
A proposition is said to be primitive if it cannot be broken down
into simpler propositions, that is, if it is not composite.
Examples: a) “The sun is shining today and it is colder than
yesterday”
b) “Sita is intelligent and she studies every night.”
Many propositions are composites that are, composed of
sub propositions and various connectives discussed
subsequently. Such composite propositions are called
compound propositions.
.

8. Altınbaş Üniversitesi Dr. Özlem ORHAN
How to construct Propositions?
 Propositional Variables can be p, q, r, s, …
 The proposition that is always true is denoted by T and
the proposition that is always false is denoted by F.
 Compound Propositions; constructed from logical
connectives and other propositions

9. Altınbaş Üniversitesi Dr. Özlem ORHAN
LOGICAL OPERATIONS OR LOGICAL CONNECTIVES
The phrases or words which combine simple statements are
called logical connectives.
 There are five types of connectives.
 Namely, ‘not’, ‘and’, ‘or’, ‘if…then’, iff
etc.
 Negation ¬
 Conjunction ∧
 Disjunction ∨
 Implication →
 Biconditional ↔

10. Altınbaş Üniversitesi Özlem ORHAN
In the following table we list some connectives, their symbols
& the nature of the compound statement formed by them.
Connective Symbol Compound statement
AND  Conjunction
OR  Disjunction
NOT  Negation
If…then  Conditional or
implication
If and only if (iff)  Biconditional

11. Altınbaş Üniversitesi Dr. Özlem ORHAN
Conjunction (AND)
Since, p ∧ q is a proposition it has a truth
value and this truth value depends only on
the truth values of p and q.
The conjunction of propositions p and q is denoted by p ∧ q
Specifically, if p & q are true then p ∧ q is
true; otherwise p ∧ q is false.

12. Altınbaş Üniversitesi Dr. Özlem ORHAN
p q p ∧ q
T T T
T F F
F T F
F F F
The truth table of p ∧ q is like this:
Example: Let p:“I am at home.”
and q :“It is raining.”
then p ∧q: “I am at home and it is raining.”

13. Disjunction (OR)
The disjunction of propositions p and q is denoted by p
∨q.
The truth value of p ∨q depends only on the truth values of
p and q. Specifically if p and q are false then p ∨q is false,
otherwise p ∨q is true.
Any two statements can be connected by the word ‘or’
to form a compound statement called disjunction.

14. The truth table for disjunction is as follows.
p q p ∨q
T T T
T F T
F T T
F F F

15. Altınbaş Üniversitesi Özlem ORHAN
Example: Let p: “I am at home.”
and q: “It is raining.”
then p ∨q: “I am at home or it is raining.”
Example: Let p: Paris is in France
q: 2 + 3 = 6
then p ∨q : Paris is in France or 2 + 3 = 6.
Here p ∨q is true since p is true & q is False.
Thus, the disjunction p ∨q is false only when p and q are
both false.

16. Negation (NOT)
The negation of a proposition p is denoted by ¬p
Symbolically, ¬p read as “not p” denotes the negation of p.
If p is true then ¬p is false and if p is false then ¬p is true.
Given any proposition P, another proposition, called
negation of P, can be formed by modifying it by “not”.

17. The truth table for Negation is as follows:
Example: Let p : “The earth is round.”,
then ¬p : “It is not the case that the earth is round,” or more
simply “The earth is not round.”
p ¬p
T F
F T

18. Altınbaş Üniversitesi Dr. Özlem ORHAN
Conditional or Implication: (If…then)
If two statements are combined by using the logical
connective ‘if…then’ then the resulting statement is called a
conditional statement.
If p and q are two statements forming the implication
“if p then q” then we denotes this implication p  q .
In the implication p  q , p is called antecedent or
hypothesis q is called consequent or conclusion.

19. Altınbaş Üniversitesi Dr. Özlem ORHAN
p q p →q
T T T
T F F
F T T
F F T
The truth table for implication is as
follows.
The statement p  q is true in all cases except when p
is true and q is false.

20. Altınbaş Üniversitesi Dr. Özlem ORHAN
Example: Let p: “I am at home.”
q : “It is raining.”
p →q : “If I am at home then it is raining.”
In p →q , p is the hypothesis (antecedent or premise) and
q is the conclusion (or consequence).

21. Altınbaş Üniversitesi Dr. Özlem ORHAN
In p →q there does not need to be any connection
between the antecedent or the consequent. The
“meaning” of p →q depends only on the truth values of
p and q.
Understanding Implication

22. Altınbaş Üniversitesi Dr. Özlem ORHAN
The statement p  q is true in all cases
except when p is true and q is false.
 “If I am elected, then I will lower taxes.”
 “If you get 100% on the final, then you will get an A.”
 If the politician is elected and does not lower taxes,
then the voters can say that he or she has broken the
campaign pledge.
 Something similar holds for the professor.
Therefore, t.his corresponds to the case where p is true
and q is false.

23. Altınbaş Üniversitesi Dr. Özlem ORHAN

24. Altınbaş Üniversitesi Dr. Özlem ORHAN

25. Altınbaş Üniversitesi Dr. Özlem ORHAN

26. The Connective Or in English
 In English “or” has two distinct meanings.
 “Inclusive Or” - In the sentence “Students who have taken CS202 or
Math120 may take this class,” we assume that students need to have taken
one of the prerequisites, but may have taken both. This is the meaning of
disjunction. For p ∨q to be true, either one or both of p and q must be true.
 “Exclusive Or” - When reading the sentence “Soup or salad comes with this
entrée,” we do not expect to be able to get both soup and salad. This is the
meaning of Exclusive Or (Xor). In p ⊕ q , one of p and q must be true, but
not both. The truth table for ⊕ is:
p q p ⊕q
T T F
T F T
F T T
F F F

27. Understanding Implication (cont)
 One way to view the logical conditional is to think of
an obligation or contract.
 “If I am elected, then I will lower taxes.”
 “If you get 100% on the final, then you will get an A.”
 If the politician is elected and does not lower taxes,
then the voters can say that he or she has broken the
campaign pledge. Something similar holds for the
professor. This corresponds to the case where p is true
and q is false.

28. Different Ways of Expressing p →q
if p, then q p implies q
if p, q p only if q
q unless ¬p q when p
q if p
q whenever p p is sufficient for q
q follows from p q is necessary for p
a necessary condition for p is q
a sufficient condition for q is p

29. Converse, Contrapositive, and Inverse
 From p →q we can form new conditional statements .
 q →p is the converse of p →q
 ¬q → ¬ p is the contrapositive of p →q
 ¬ p → ¬ q is the inverse of p →q
Example: Find the converse, inverse, and contrapositive of
“It raining is a sufficient condition for my not going to
town.”
Solution:
converse: If I do not go to town, then it is raining.
inverse: If it is not raining, then I will go to town.
contrapositive: If I go to town, then it is not raining.

30. Biconditional
 If p and q are propositions, then we can form the biconditional
proposition p ↔q , read as “p if and only if q .” The biconditional
p ↔q denotes the proposition with this truth table:
 If p denotes “I am at home.” and q denotes “It is raining.” then
p ↔q denotes “I am at home if and only if it is raining.”
p q p ↔q
T T T
T F F
F T F
F F T

31. Expressing the Biconditional
 Some alternative ways “p if and only if q” is expressed
in English:
 p is necessary and sufficient for q
 if p then q , and conversely
 p iff q

32. Truth Tables For Compound
Propositions
 Construction of a truth table:
 Rows
 Need a row for every possible combination of values for
the atomic propositions.
 Columns
 Need a column for the compound proposition (usually
at far right)
 Need a column for the truth value of each expression
that occurs in the compound proposition as it is built
up.
 This includes the atomic propositions

33. Example Truth Table
 Construct a truth table for
p q r r p  q p  q → r
T T T F T F
T T F T T T
T F T F T F
T F F T T T
F T T F T F
F T F T T T
F F T F F T
F F F T F T

34. Equivalent Propositions
 Two propositions are equivalent if they always have the
same truth value.
 Example: Show using a truth table that the
conditional is equivalent to the contrapositive.
Solution:
p q ¬ p ¬ q p →q ¬q → ¬ p
T T F F T T
T F F T F F
F T T F T T
F F T T T T

35. Using a Truth Table to Show Non-
Equivalence
Example: Show using truth tables that neither the
converse nor inverse of an implication are not
equivalent to the implication.
Solution:
p q ¬ p ¬ q p →q ¬ p →¬ q q → p
T T F F T T T
T F F T F T T
F T T F T F F
F F T T T T T

36. Problem
 How many rows are there in a truth table with n
propositional variables?
Solution: 2n We will see how to do this in Chapter 6.
 Note that this means that with n propositional
variables, we can construct 2n distinct (i.e., not
equivalent) propositions.

37. Precedence of Logical Operators
Operator Precedence
 1


2
3


4
5
p q  r is equivalent to (p q)  r
If the intended meaning is p (q  r )
then parentheses must be used.