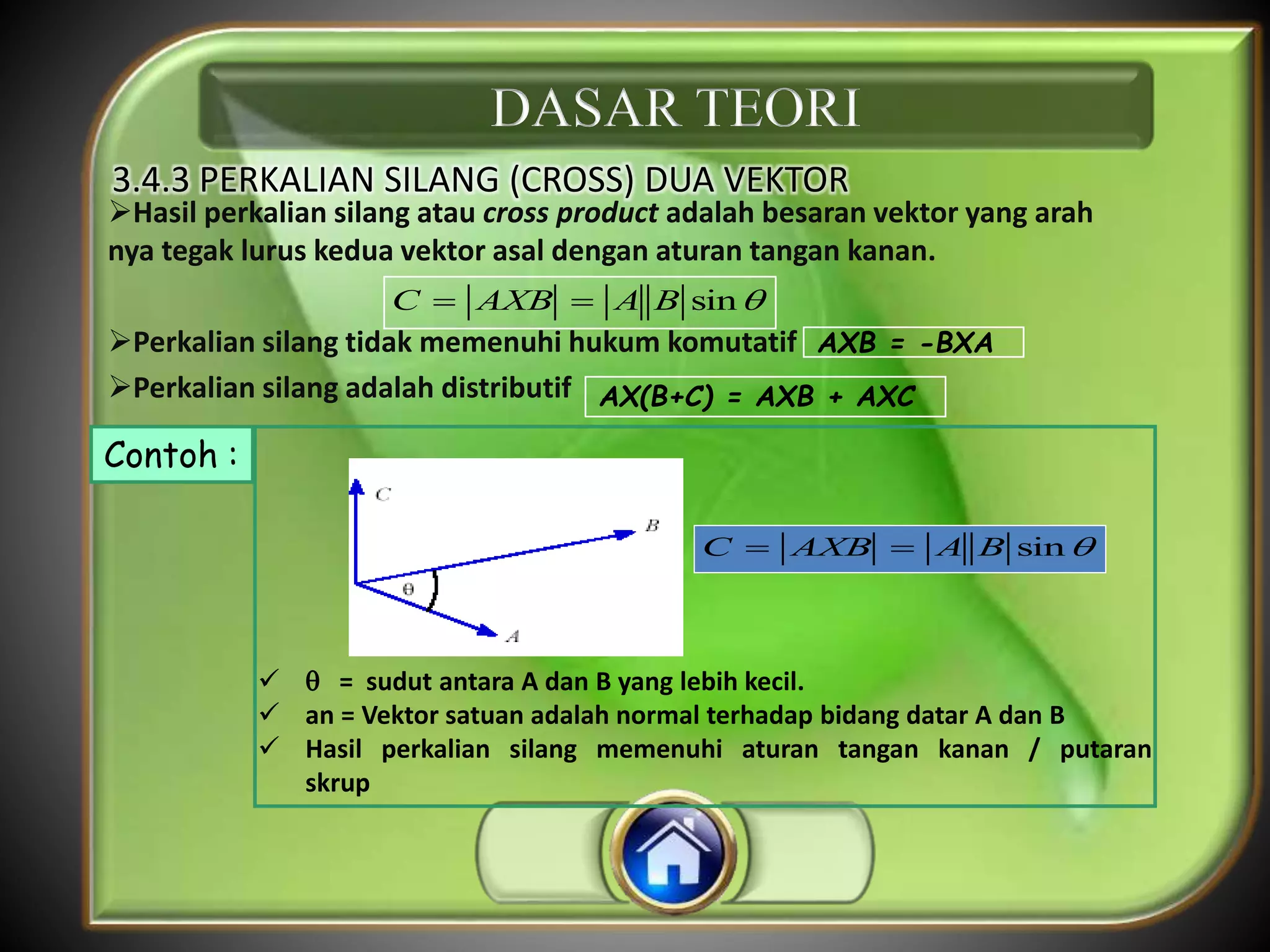
Dokumen tersebut membahas tentang besaran, satuan, dan vektor dalam fisika. Secara ringkas, besaran adalah hal-hal yang dapat diukur dengan satuan tertentu, satuan digunakan sebagai standar pengukuran, sedangkan vektor digunakan untuk menggambarkan perpindahan dan gaya.