Dokumen tersebut membahas tentang dimensi dan analisis dimensi. Dimensi adalah cara menuliskan suatu besaran fisika dengan menggunakan simbol besaran pokok seperti panjang, massa dan waktu. Ada dua jenis dimensi yaitu dimensi primer dan sekunder. Analisis dimensi digunakan untuk menentukan satuan besaran turunan dan menguji kebenaran hubungan antar besaran fisika.

1. DIMENSI DAN ANALISIS
DIMENSI
Nama Kelompok 4:
1.
2.
3.
4.
5.
6.
Dicky Pratama
(06)
Dimas Aditya P.
(07)
Elina Sari
(08)
Ichlasul Amal
Laura Mahdalena
Satria Bintang M.
(15)
(18)
(28)

2. DIMENSI

3.  Dimensi
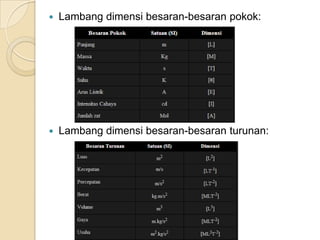
 Dimensi adalah cara penulisan suatu besaran
dengan menggunakan simbol (lambang) besaran
pokok. Hal ini berarti dimensi suatu besaran
menunjukkan cara besaran itu tersusun dari
besaran-besaran pokok.
 Ada dua macam dimensi yaitu Dimensi Primer
dan Dimensi Sekunder.
o Contoh dimensi primer :
• [M] (untuk satuan massa)
• [L] (untuk satuan panjang)
• [T] (untuk satuan waktu)
o Contoh dimensi sekunder :
• [M] [L]-3 (untuk satuan massa jenis)
• [L] [T]-2 (untuk satuan percepatan)

4. Cara Menentukan Dimensi
Contoh :
• Volume
Volume balok adalah hasil kali dari
panjang, lebar, tinggi yang ketiganya memiliki dimensi
panjang. Maka dimensi volume:
[volume] = [panjang] [lebar] [tinggi]
= [L] [L] [L]
= [L]3
• Massa Jenis
Massa Jenis adalah hasil bagi dari massa dan volume.
Maka dimensi massa jenis:
[massa jenis] = [massa] / [volume]
= [M] / [L]3
= [M] [L]-3

5. 
Lambang dimensi besaran-besaran pokok:

Lambang dimensi besaran-besaran turunan:

6. ANALISIS
DIMENSI

7. Analisis Dimensi


Analisis dimensi adalah suatu cara untuk
menentukan satuan dari suatu besaran
turunan, dengan cara memerhatikan dimensi
besaran tersebut.
Manfaat analisis dimensi :
1) Dapat digunakan untuk membuktikan dua besaran
fisika setara atau tidak. Dua besaran fisika hanya
setara jika keduanya memiliki dimensi yang sama dan
keduanya termasuk besaran skalar atau keduanya
termasuk besaran vektor
 Contoh : Buktikan bahwa besaran usaha (W) memiliki
kesetaraan dengan besaran energi kinetik (Ek)!
Diketahui besaran usaha (W) adalah [M][L]2[T]-2
Rumus
Angka setengah pada persamaan energi kinetik merupakan

8. [e. kinetik] = [massa] [kecepatan]2
= [M] ([L] [T]-1)2
= [M] [L]2 [T]-2
2)
Jadi, karena nilai dimensi usaha (W) dan energi kinetik
(Ek) sama, maka hal ini menunjukkan bahwa besaran
usaha memiliki kesetaraan dengan besaran energi
kinetik.
Dapat digunakan untuk menentukan persamaan
yang pasti salah atau mungkin benar.
• Contoh: Manakah hubungan yang benar antara x=at atau
x=at2 ?
Jika x=jarak , a=percepatan, t=waktu. Diketahui jarak adalah
besaran panjang yangmemiliki dimensi [L], percepatan
memiliki dimensi [L]/[T2], dan waktu memiliki dimensi [T].
Maka:
x=at
[L] = [L]/[T2]. [T]
[L] = [L]/[T]

9. Sedangkan:
x = at2
[L] = [L]/[T2]. [T]2
ternyata x dan at2 memiliki dimensi sama, yaitu
[L]/[T], berarti secara dimensional persamaan x =
at2 adalah benar!

10. 3)
Dapat digunakan untuk menurunkan persamaan
suatu besaran fisika jika kesebandingan besaran
fisika tersebut dengan besaran-besaran fisika
lainnya diketahui
• Contoh: Perhatikan gerak melingkar horizontal yang ditempuh
sebuah batu yang diikat pada ujung seutas tali. Kita anggap
bahwa gaya tegang F dalam kawat memiliki kesebandingan
dengan besaran-besaran berikut: massa batu m, kelajuan
batu v, dan jari-jari lintasan r. Tentukan persamaan gaya
tegang dalam kawat (F).
Jawab :
Kita dapat menulis persamaan gaya tegang dalam kawat
sebagai :
F = kmxvyrz …………… (*)
Dimana x, y, z adalah pangkat yang tak diketahui dan k adalah
tetapan tanpa dimensi. Selanjutnya dengan menggunakan
prinsip dimensi ruas kiri = dimensi ruas kanan, kita bisa
menghitung nilai x, y, z dan akhirnya menemukan persamaan
gaya tegang dalam kawat.

11. Maka:
Dimensi gaya F adalah [M][L][T]-2, dimensi massa m adalah
[M], dimensi kelajuan v adalah [L][T]-1, dimensi jari –
jari r adalah [L].
F = kmxvyrz
[F] = k[m]x[v]y[r]z
[M][L][T]-2 = [M]x([L][T]-1)y[L]z
(k tak berdimensi)
[M]1[L]1[T]-2 = [M]x[L]y + z[T]-y
Supaya dimensi ruas kanan dan kiri sama, maka pangkat dari
[M], [L], [T] dikedua ruas harus sama. Kita peroleh :
Pangkat [M] : 1 = x
x=1
Pangkat [T] : -2 = -y
y=2
Pangkat [L] : 1 = y + z
1=2+z
z = -1
Masukkan nilai x, y, z di atas ke dalam persamaan
(*), sehingga akan kita peroleh persamaan gaya tegang tali :
F = km1v2r-1
atau
F = kmv2/r