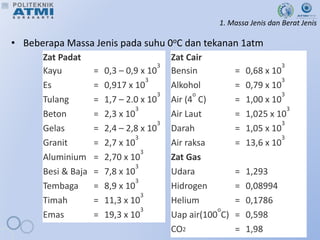
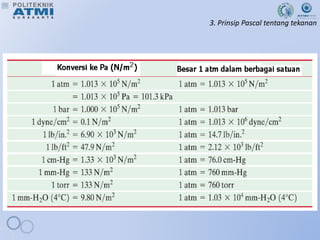
Dokumen ini membahas mekanika fluida dalam konteks fisika dasar, mencakup topik seperti massa jenis, tekanan atmosfer, hukum Archimedes, dan prinsip Pascal. Poin-poin penting meliputi definisi massa jenis, tekanan, serta aplikasi hukum-hukum fisika tersebut dalam situasi nyata, seperti pada dongkrak hidrolik dan gaya apung. Ujian tengah semester dijadwalkan untuk minggu depan.

1. Fisika Dasar Semester II
TMI, TMK, TPM
3. Mekanika Fluida
(Pertemuan 5-7)
Andre Sugijopranoto SJ

2. Isi Kuliah
1. Massa jenis dan berat jenis
2. Tekanan atmosfer dan tekanan ukur
3. Prinsip Pascal tentang tekanan
4. Hukum Archimedes
5. Persamaan Bernoulli
Kuliah hari Selasa – Kamis – Selasa
Hari Kamis minggu depan: Ujian Tengah Semester.

3. 1. Massa Jenis dan Berat Jenis
• 3 Jenis fase zat:
– Padat : bentuk dan ukuran/volume relatif tetap
– Cair: bentuk mengikuti tempatnya, volume relatif tetap
– Gas: bentuk dan volume berubah-ubah mengikuti tempatnya
Catatan: sebenarnya ada bentuk zat yang lain, misalnya : plasma (elektron
dilepaskan dari intinya), kristal (dalam TV, monitor, kalkulator, arloji digital,
dlsb)
• Fluida: kumpulan molekul yang ikatan di antaranya lemah
sehingga mudah berubah bentuk. Fluida meliputi zat cair dan gas.
• Massa Jenis (= ρ /rho)
massa per satuan volume
Satuan: kg/m3
v
m



4. 1. Massa Jenis dan Berat Jenis
• Beberapa Massa Jenis pada suhu 0oC dan tekanan 1atm
Zat Padat Zat Cair
Kayu = 0,3 – 0,9 x 10
3
Bensin = 0,68 x 10
3
Es = 0,917 x 10
3
Alkohol = 0,79 x 10
3
Tulang = 1,7 – 2.0 x 10
3
Air (4
o
C) = 1,00 x 10
3
Beton = 2,3 x 10
3
Air Laut = 1,025 x 10
3
Gelas = 2,4 – 2,8 x 10
3
Darah = 1,05 x 10
3
Granit = 2,7 x 10
3
Air raksa = 13,6 x 10
3
Aluminium = 2,70 x 10
3
Zat Gas
Besi & Baja = 7,8 x 10
3
Udara = 1,293
Tembaga = 8,9 x 10
3
Hidrogen = 0,08994
Timah = 11,3 x 10
3
Helium = 0,1786
Emas = 19,3 x 10
3
Uap air(100
o
C) = 0,598
CO2 = 1,98

5. 1. Massa Jenis dan Berat Jenis
• Specific Gravity (SG) = Berat Jenis
– Perbandingan massa jenis zat cair terhadap massa jenis air pada suhu 4oC
(ρair= 1000 kg/m3)

6. 2. Tekanan atmosfer dan tekanan ukur
• Tekanan (=P)
– Tekanan = besar gaya per satuan luas
P = F/A
F = gaya yang tegak lurus dengan suatu luasan A
Satuan: N/m2 = Pascal (Pa)
• Soal: Satu orang beratnya 60 kg. Luas 2 telapak kakinya = 500 cm2.
Berapa tekanan 2 telapak kaki pada lantai? Apabila orang tersebut
berdiri dengan 1 kaki, berapa tekanan telapak kaki pada lantai?
P = F/ A = m.g / A = 60. 9,8 / 0,05 m2 = 11.760 N/m2
Dengan satu kaki: P = m.g / ½ A = 60. 9,8 / 0,025 m2 = 23.520 N/m2
• Tekanan dalam cairan karena cairan itu sendiri
P = F/A = m.g/A = ρ. V.g/A = ρ. A.h.g/A = ρ.g.h
h = ketinggian cairan
P = ρ.g.h

7. 2. Tekanan atmosfer dan tekanan ukur
Soal: Permukaan air dalam tangki air
adalah 30 m di atas keran air dalam
dapur sebuah rumah. Berapakah
perbedaan tekanan air antara
permukaan air dalam tangki dan pada
keran air?
P =ρ.g.h = 1. 103. 9,8. 30 = 294000 N/m2
Soal: Berapakah gaya yang mengenai genderang
telinga orang yang berenang pada kedalaman 5 m di
bawah air? Luas genderang telinga diperkirakan
1cm2.
Beda tekanan di permukaan air dan 5 m di bawah air
P =ρ.g.h = 1. 103 . 9,8. 5 = 49.000 Pa
F = P. A = 49.000 x 1. 10-4 = 4,9 N.
 Gaya ini yang membuat telinga terasa sakit.

8. 2. Tekanan atmosfer dan tekanan ukur
TEKANAN ATMOSFER
• Tekanan atmosfer itu berbeda-beda tergantung tempat dan cuaca
• Pada tempat dengan ketinggian 0 m di atas permukaan air laut,
tekanan atmosfer adalah 1,013. 105 N/m2
– 1 atm = 1,013. 105 N/m2 = 101,3 kPa
– Satuan lain = bar  1 bar = 105 N/m2
TEKANAN UKUR
– Besarnya = besar gaya yang tegak lurus dengan suatu luasan:
satuan luas
P = F/A
– Satuan: N/m2 = Pascal (Pa)
– Apabila kita mengukur tekanan sesuatu (ban misalnya), hasil dari ukuran
adalah tekanan ukur.
Tekanan absolut P = jumlah tekanan atmosfer dan tekanan ukur.

9. 2. Tekanan atmosfer dan tekanan ukur
Soal: Dalam bejana U terdapat minyak dan air dalam
keadaan stabil. Air di sebelah kanan dan minyak
di sebelah kiri. Massa jenis air = 998 kg/m3. Tinggi
l = 135 mm dan d = 12 mm. Berapakah massa
jenis minyak?
Jawab:
Tekanan di titik B = PB = P0 + ρair.g.l
Tekanan di titik A = PA = P0 + ρminyak.g. (l + d)
Karena keadaan stabil, maka PA = PB
 P0 + ρair.g.l = P0 + ρminyak.g. (l + d)
ρminyak = ρair. = 998 = 916,5306 kg/m3
d
l
l
 12
135
135


10. 3. Prinsip Pascal tentang tekanan
• Hukum Pascal: Tekanan yang diberikan pada zat cair di dalam
ruang tertutup akan diteruskan ke segala arah dan semua bagian
ruang tersebut dengan sama besar.
• Penerapan Hukum Pascal: dongkrak hidrolik,
pompa hidrolik, rem hidrolik, mesin
pengepres hidrolik. Prinsip ini digunakan
karena dapat memberikan gaya yang kecil untuk
menghasilkan gaya yang besar.

11. 3. Prinsip Pascal tentang tekanan
• Prinsip Dongkrak Hidrolik
Gaya F1 dikenakan pada piston A1. Zat cair
menekan ke atas sebesar PA1. Tekanan ini
diteruskan ke piston A2. Ketinggian
PistonA1 = PistonA2.
PA1 = PA2  =
F2= F1
Gaya yang dihasilkan oleh F1 sebesar perbandingan luas 2 piston
2
2
1
1
A
F
A
F

1
2
1
2
F
F
A
A

1
2
A
A

12. 3. Prinsip Pascal tentang tekanan
Contoh soal:
Dongkak untuk menaikan mobil mempunyai
Piston dengan jari-jari 5 cm. Tekanan udara
dimasukan ke dalam piston dan dialirkan
lewat cairan ke piston lain ber jari-jari 15 cm.
Seandainya dongkrak harus mengangkat
sebuah mobil seberat 13.300 N, berapakah
tekanan yang harus dimasukan ke dalam piston yang kecil?
F1 = F2
F1 = 13.300 = 13.300 x 0,1111 = 1.477,78 N
Tekanan = P1 = = = 188.252,2293 Pa
1
1
A
F
2
A
1
A
2
2
)
15
,
0
(
)
05
,
0
(


2
)
05
,
0
(
1.477,78


13. 3. Prinsip Pascal tentang tekanan
Mengukur Besar Tekanan
Manometer
• Berbentuk pipa U
• Sebagian diisi dengan cairan, bisa air atau Hg
• Tekanan yang diukur P berhubungan dengan
perbedaan tinggi permukaan cairan h
P = P0 + ρ.g.h
• Tekanan kadang-kadang diukur hanya perubahan tinggi h saja
yang disebutkan. Yang paling lazim adalah, tekanan dinyatakan
dalam mm Hg (air raksa). 1 mm Hg = 133 N/m2 (Pa). 1 mm Hg
sering disebut sebagai torr.

14. 3. Prinsip Pascal tentang tekanan

15. 4. Hukum Archimedes
• Gaya Apung
Benda yang dimasukan ke dalam cairan terasa lebih
ringan di bandingkan pada saat tidak berada dalam
cairan.
Gaya gravitasi terjadi pada benda dengan
arah ke bawah, sedangkan gaya apung terjadi ke
arah atas.
Benda silinder dengan tinggi h dimasukkan seluruhnya ke dalam
cairan. Luas permukaan atas = luas permukaan bawah = A. Massa
jenis cairan = ρ.
Tekanan cairan pada bagian atas silinder = P1 = ρ.g.h1.
Gaya pada bagian atas silinder = F1 = P1. A = ρ.g.h1.A.
Gaya pada bagian bawah silinder = F2 = P2. A = ρ.g.h2.A.
Gaya apung Fb = F2-F1

16. 4. Hukum Archimedes
Gaya apung Fb = F2-F1
= ρ.g.h2.A - ρ.g.h1.A
= ρ.g.A (h2-h1)
= ρ.g.A.h
= ρ.g.V
= m.g
m = massa cairan dengan volume sebesar volume benda
= massa cairan yang dipindahkan benda.
Gaya apung pada silinder = berat cairan yang dipindahkan oleh
silinder
Rumus ini ditemukan oleh Archimedes (287 – 212 SM) movie
Gaya apung pada sebuah obyek yang dimasukan ke dalam cairan
sama dengan berat cairan yang dipindahkan oleh obyek tersebut

17. 4. Hukum Archimedes
Hk Archimedes dengan Hk Newton
Benda D di masukan ke dalam tabung berisi air. Dalam
keadaan seimbang, gaya yang ada (gambar a) adalah:
1. Gaya berat benda D = m.g (ke bawah)
2. Gaya apung sebesar FB (ke atas)
Lihat gambar b:
Kita membayangkan sebuah bentuk dan ukuran yang
sama dengan benda D terbuat dari air itu sendiri dan
kita sebut D’. Posisi D’ persis sama seperti D. Maka gaya
apung benda D’ besarnya persis sama dengan gaya
apung benda D (ingat Fb = F2-F1). FB = m’.g.
Jadi, FB besarnya = berat cairan yang volume nya =
volume benda yang dimasukan ke dalam cairan.
FB = m’.g = m.g  m’ = m

18. 4. Hukum Archimedes
Contoh Soal:
Sebuah batu seberat 70 kg berada di dasar laut. Volume batu adalah
30.000 cm3. Berapa gaya yang dibutuhkan untuk mengangkat batu dari
dasar laut? Massa jenis air laut = 1025 kg/m3.
Gaya yang dibutuhkan untuk mengangkat batu adalah
F = m.g – gaya apung
Gaya apung = mair laut.g = ρair laut. Vbenda.g = 1025. 0,03 m3. 9,8 = 301,35N
F = 70. 9,8 - 301,35 = 384,65 N
Di dalam air, batu seolah-olah massanya = 384,65 / 9.8 = 39,25 kg

19. 4. Hukum Archimedes
Contoh Soal:
Mahkota raja massanya 14,7 kg. Di dalam air, massanya adalah 13,4 kg.
Apakah mahkota raja terbuat dari emas murni? Berat jenis emas = 19,3.
Berat di dalam air = w’ yang sama dengan
Gaya tegangan tali timbangan F’T
w’ = F’T = w – FB
w - w’ = FB = m.g = ρair.Vmahkota.g
14,7 - 13,4 = ρair.Vmahkota.g
ρair.Vmahkota.g = 1,3
Vmahkota = 1,3 /ρair. g --- (persamaan 1)
w = m.g = ρmahkota.Vmahkota.g
14,7 = ρmahkota.Vmahkota.g
Persamaan 1  14,7 = ρmahkota. 1,3 /(ρair. g) .g
14,7 = 1,3 ρmahkota /ρair ρmahkota /ρair = 11,3077  bukan emas

20. 4. Hukum Archimedes
• Benda Mengapung
Hukum Archimedes berlaku juga untuk benda-benda yang mengapung
dalam cairan.
Benda mengapung dalam cairan apabila ρbenda < ρcairan
Pada saat benda mengapung dan diam, maka gaya apung = berat
benda.
Contoh: balok kayu dengan BJ = 0,6 dan volumenya
2m3. Maka massa balok kayu = 600 x 2 = 1.200 kg.
Berat kayu = 1200 x 9,8 = 11.760 N.
Saat balok ada di dalam air seluruhnya, air yang
dipindahkan = 2m3 = 2000 kg. Gaya apung = 2000 x
9,8 = 19.600 N. Gaya apung > berat balok kayu.
Balok kayu terdorong ke atas dan mengapung.
Balok kayu mencapai kesetimbangan saat gaya apung = berat balok.
Berat air yang dipindah harus = 1200 kg = 1,2 m3. Vol ini = 1,2/2 = 60%
volume balok. Jadi 60% balok tenggelam dan 40% ada di atas air.

21. 4. Hukum Archimedes
FB = m.g
ρcairan. Vcairan yg dipindah. g = ρbenda. Vbenda. g
ρcairan. Vcairan yg dipindah = ρbenda. Vbenda
Hidrometer
Alat pengukur BJ cairan dengan cara mengukur seberapa dalam
Hidrometer tenggelam dalam cairan tersebut
cairan
benda
benda
cairan
V
V




22. 4. Hukum Archimedes
Sebuah hidrometer panjangnya 25 cm dan luas penampang 2cm2
beratnya 45 gr. Di manakah tanda angka 1 harus diletakan saat
hidrometer dimasukan ke dalam air?
ρ = 900 kg/m3
ρair = 1000 kg/m3
Vcairan yg dipindah = 0,9 Vbenda
Panjang hidrometer yang tenggelam = 0,9 panjangnya = 0,9x25 cm =
22,5 cm.


0002
,
0
.
25
,
0
045
,
0
V
m
cairan
benda
benda
cairan
V
V




23. 5. Persamaan Bernoulli
Fluida yang Bergerak
Kecepatan fluida berubah pada saat ukuran
tempatnya berubah
Laju massa fluida =
volume fluida yang melewati luasan A1 sejauh L1 selama t = A1 . L1
Kecepatan fluida adalah v1 =
Laju massa fluida = = = = ρ1.A1.v1
Karena fluida tidak ditambah dan dikurangi dalam tabungnya, maka
laju massa fluida di titik A1 dan A2 tetap sama
 ρ1.A1.v1 = ρ2.A2.v2  persaman kontinuitas
t
m


t
l1


t
m


t
V1
1



t
l
.
A
. 1
1
1



t
m
t
m 2
1






24. 5. Persamaan Bernoulli
Contoh soal: air mengalir dari kran. Diameter
lubang kran = A0 = 1,2 cm2. Dalam jarak 4,5 cm
Luas permukaan air menjadi A = 0,35 cm2.
Berapakah kecepatan air saat keluar dari kran?
ρ0.A0.v0 = ρ.A.v
Besar ρ sama  A0.v0 = A.v -- (persamaan 1)
Air bergerak menempuh jarak h = 4,5 cm
S = Vo.t + ½ a.t2
V = V0 + a.t  a = g
v2 = vo
2 + 2.g.h -- (persamaan 2)
Persamaan 1 dan 2 
V0=0,286 m/s
2
2
0
2
0
A
A
ghA
2
v



25. 5. Persamaan Bernoulli
Prinsip Hukum Bernoulli
• Pada saat suatu fluida mempunyai kecepatan tinggi, maka
tekanannya menjadi rendah; pada saat mempunyai kecepatan
rendah maka tekanannya menjadi tinggi.
Persamaan Bernoulli
P + ½ ρ.v2 + ρ.g.y = konstan
atau:
P1 + ½ ρ.v1
2 + ρ.g.y1 = P2 + ½ ρ.v2
2 + ρ.g.y2
ρ = massa jenis cairan
V = kecepatan aliran
g = percepatan gravitasi
y = tinggi titik dari suatu referensi/datum

26. 5. Persamaan Bernoulli
Contoh Soal: Sistem pipa di dalam rumah.
Air dipompa dengan tekanan 3atm dan
kecepatan 0,5 m/s pada pipa dengan ф 4 cm
di atas permukaan tanah. Berapakah
kecepatan dan tekanan air di pipa kamar
mandi di lantai 2 yang tingginya 5 m dari
permukaan tanah? Pipa tidak memiliki
cabang.
Persamaan kontinuitas
ρ1.A1.v1 = ρ2.A2.v2 karena fluidanya sama maka ρ1 = ρ2
A1.v1 = A2.v2  =1,1834 m/s
Persamaan Bernoulli
PA + ½ ρ.vA
2 + ρ.g.yA = PB + ½ ρ.vB
2 + ρ.g.yB
2
2
2
2
2
1
1
2
1
1
2
)
013
,
0
(
)
02
,
0
(
5
,
0
r
r
v
A
A
v
v 





27. 5. Persamaan Bernoulli
PB = PA + ½ ρ(vA
2 - vB
2) + ρ.g (yA- yB)
PB = 3. 105 N/m2 + ½ 1000 (0,522 - 1,18342) + 1000. 9,8 (0-5)
PB = 3. 105 – 565,0178 – 49000 = 250434,9822 N/m2 = 2,5043 atm
Penerapan Prinsip Bernoulli
1. Teorema Torricelli
Keadaan: menghitung kecepatan fluida di titik 1
Titik 2: permukaan fluida.
Persamaan Bernoulli: P1 + ½ ρ.v1
2 + ρ.g.y1 = P2 + ½ ρ.v2
2 + ρ.g.y2
P1 = P2 = tekanan atmosphere;
kecepatan fluida di permukaan sangat kecil, dapat dianggap = 0
P1 + ½ ρ.v1
2 + ρ.g.y1 = P2 + 0 + ρ.g.y2
½ v1
2 + g.y1 = g.y2  v1 = Teorema Torricelli
)
y
y
(
g
2 1
2 

28. 5. Persamaan Bernoulli