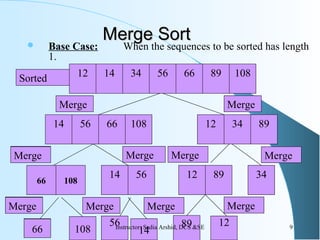
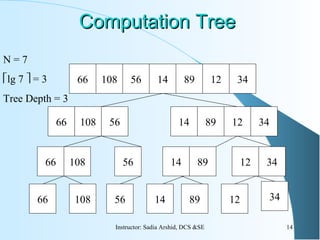
The document discusses the merge sort algorithm. It explains that merge sort uses a divide and conquer approach by recursively dividing an array into smaller sub-problems until single elements are reached, then merging the sorted sub-arrays back together into a fully sorted array. The time complexity of merge sort is O(n log n) as it divides the problem space in half at each step and requires linear time to merge the sub-arrays. While efficient, merge sort requires additional storage space proportional to n log n to perform the sorting in place.

1. Analysis of AlgorithmsAnalysis of Algorithms
Divide and Conquer Approach
1Instructor: Sadia Arshid, DCS &SE

2.  Divide the problems into a number of sub
problems.
 Conquer the sub problems by solving
them recursively. If the sub-problem
sizes are small enough, just solve the
problems in a straight forward manner.
 Combine the solutions to the sub
problems into the solution for the original
problem.
Divide and Conquer ApproachDivide and Conquer Approach
2Instructor: Sadia Arshid, DCS &SE

3. Divide-and-ConquerDivide-and-Conquer
AlgorithmsAlgorithms
 An algorithm design
– merge sort
– maxmin
– quick sort
– Matrix multiplication
 A larger problem is broken up into smaller
problems, the smaller problems are recursively,
and the results are merged together again
3Instructor: Sadia Arshid, DCS &SE

4. Divide-and-ConquerDivide-and-Conquer
AlgorithmsAlgorithms
More formally, we will consider only those
algorithms which:
– divide a problem into sub-problems, each
approximately of size n/b
– in all cases we have seen, the whole was
divided into b equal sub-problems
– solve those sub-problems recursively
– combine the solutions to the sub-problems to
get a solution to the overall problem
4Instructor: Sadia Arshid, DCS &SE

5. MERGE SORTMERGE SORT
Graphically, merge sort is represented as
follows:
Once we have sorted the shortest lists, then
we merge then back together again into a
sorted list
5Instructor: Sadia Arshid, DCS &SE

6.  Divide the n element sequence to be
sorted into two subsequences of n/2
elements each.
 Conquer: Sort the two subsequences to
produce the sorted answer.
 Combine: Merge the two sorted sub
sequences to produce the sorted answer.
Merge SortMerge Sort
6Instructor: Sadia Arshid, DCS &SE

7. Merge Sort AlgorithmMerge Sort Algorithm
procedure MergeSort(n,s)
h=n/2, m=n-h
u=array[1..h], v=array[m..n]
if n>1
copy s[1] through s[h] to u
copy s[h+1] through s[n] to v
mergesort(h,u)
mergesort(m,v)
merge(h,m,u,v,s] 7Instructor: Sadia Arshid, DCS &SE

8. procedure merge(h,m,u,v,s)
i=1,j=1,k=1
while i<=h and j<=m
if u[i]<v[j]
s[k]=u[i], i=i+1
else s[k]=v[j],j=j+1
k=k+1
if i>h
copy v[j] through v[m] to s[k] through s[h+m]
else
copy u[i] through u[h] to s[k] through s[h+m]
8Instructor: Sadia Arshid, DCS &SE

9. Merge SortMerge Sort Base Case: When the sequences to be sorted has length
1.
108 56 1214 89 3466Unsorted
108 56 1466
Divide
10866
Divide
66
Divide
66
BCase
66
Merge
108
Divide
108
BCase
108
Merge
66 108
Merge
56 14
Divide
56
Divide
56
BCase
56
Merge
14
Divide
14
BCase
14
Merge
14 56
Merge
56 66 10814
Merge
1289 34
Divide
1289
Divide
89
Divide
89
BCase
89
Merge
12
Divide
12
BCase
12
Merge
8912
Merge
34
Divide
34
BCase
34
Merge
3412 89
Merge
14 34 8956 66 10812Sorted
9Instructor: Sadia Arshid, DCS &SE

10. Merge Sort AnalysisMerge Sort Analysis
 T(n)=T[h]+T[m]+complexity of merge
 Complexity of merge: worst case, h+m-1
 Suppose n is a power of two, so that we always split
into even halves.
– h=n/2, m=n-n/2=n/2
– w(n)=w[n/2]+w[n/2]+n-1
 For n = 1 the time to merge sort is1 otherwise
 The time to merge sort n numbers is equal to the
time to do two recursive merge sorts of size n/2, plus
the time to merge, which is linear.
 Solve this recurrence to find out running time. 10Instructor: Sadia Arshid, DCS &SE

11. w(1) = 0
w(n) = 2w(n/2) + n-1
 W[n]=2w[n/2]+n-1
 W[n/2]=2w[n/4]+n/2-1
 W[n/4]=2w[n/8]+n/4-1
 By backward substitution
 W[n]=2(2w(n/4)+n/2-1)+n-1
 =22
w(n/4)+n-2+n-1
 =22
(2w(n/8)+n/4-1)+n-2+n-1
 =23
w[n/8]+n-22
+n-2+n-1
11Instructor: Sadia Arshid, DCS &SE

12.  By generalizing equation
 =2i
w[n/2i
]+in-2i-1
-2i-2
-…..-20
 =2i
w[n/2i
]+in-(2i
-1)
 By taking n=2i
 =nw[n/n]+nlgn-(n-1)
 =nlgn-(n-1)єO(nlgn)
12Instructor: Sadia Arshid, DCS &SE

13. Problem with Merge SortProblem with Merge Sort
In-place sorting ?
Space Complexity
13Instructor: Sadia Arshid, DCS &SE

14. Computation TreeComputation Tree
108 56 1214 89 3466
108 56 1466 1289 34
10866 56 14 1289 34
66 108 56 14 89 12
N = 7
lg 7  = 3
Tree Depth = 3
34
14Instructor: Sadia Arshid, DCS &SE

15. at each level total number of items are n
and total recursive calls are lg n(depth of
tree)
so total space complexity is nlgn
15Instructor: Sadia Arshid, DCS &SE

16. Other version of MERGEOther version of MERGE
SORTSORT
procedure MergeSort2(low,high,n,s)
if low<high
mid=(low+high)/2
mergesort2(low,mid)
mergesort2(mid+1,high)
merge2(low,mid,high]
16Instructor: Sadia Arshid, DCS &SE

17. procedure merge2(low,mid,high)
i=low,j=mid,h=low
while h<=mid and j<=high
if s[h]<s[j]
u[i]=s[h], h=h+1
else u[i]=s[j], j=j+1
i=i+1
if i>h
copy s[h] through s[mid] to u[i] to u[high]
else
copy s[j] through s[high] to u[i] to u[high]
17Instructor: Sadia Arshid, DCS &SE

18. time complexity???
space complexity???
18Instructor: Sadia Arshid, DCS &SE