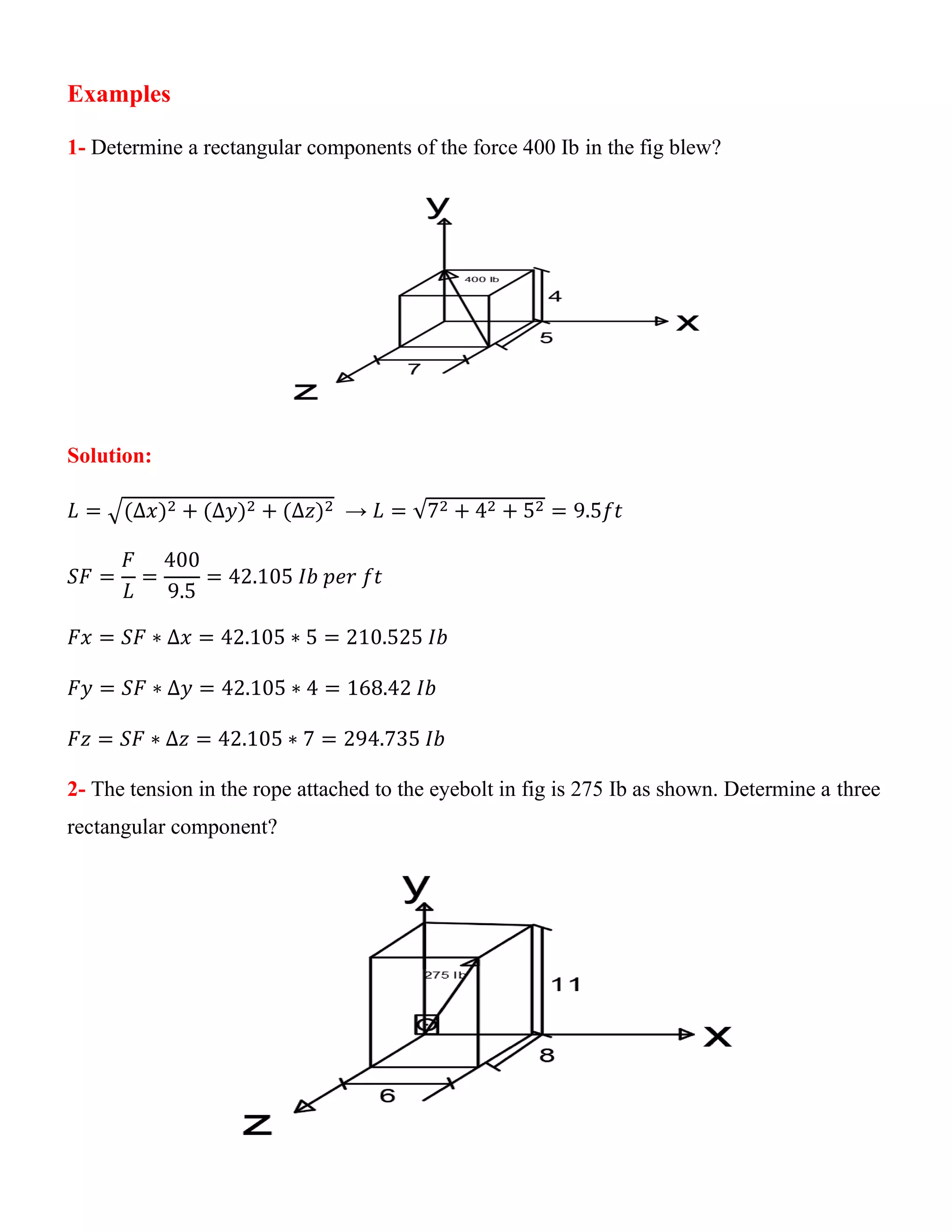
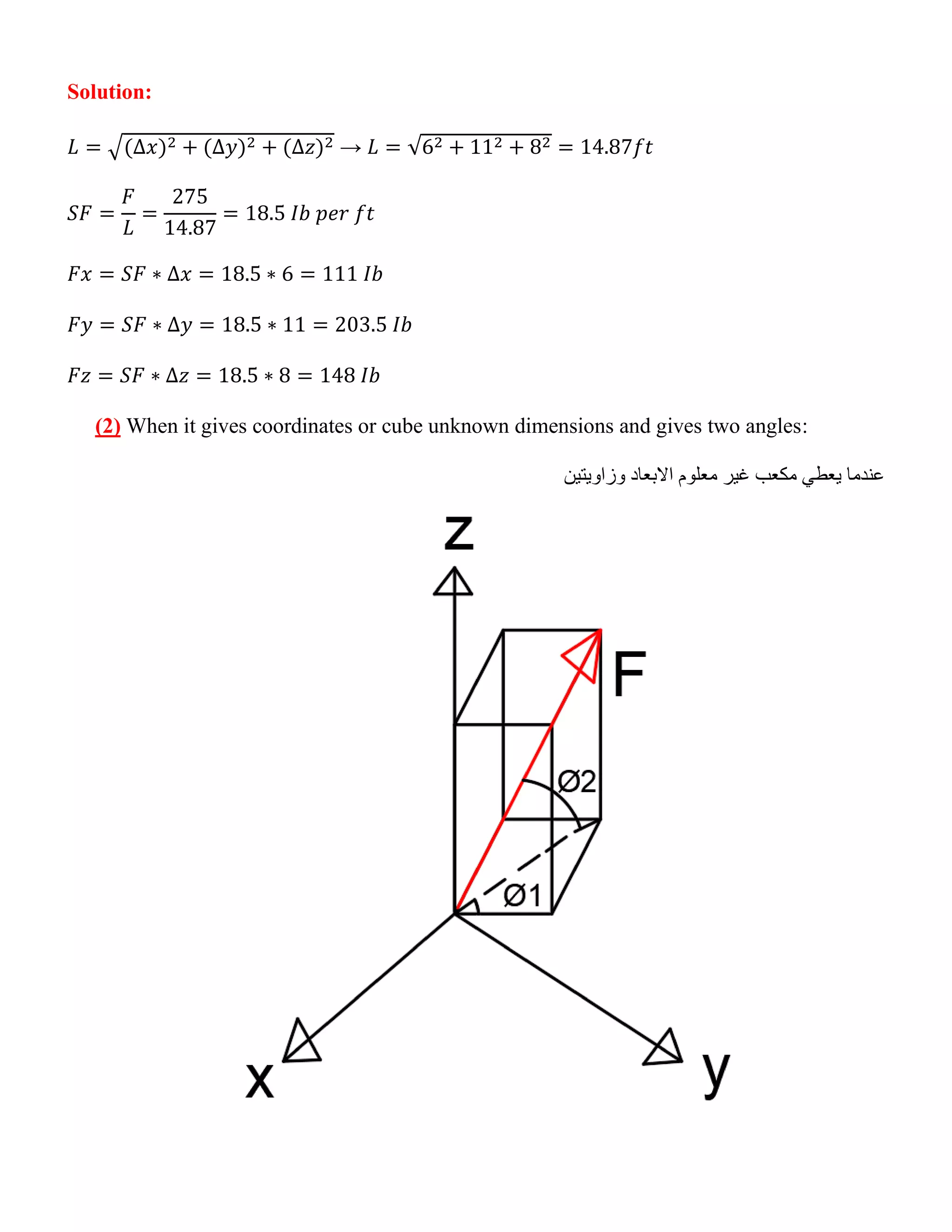
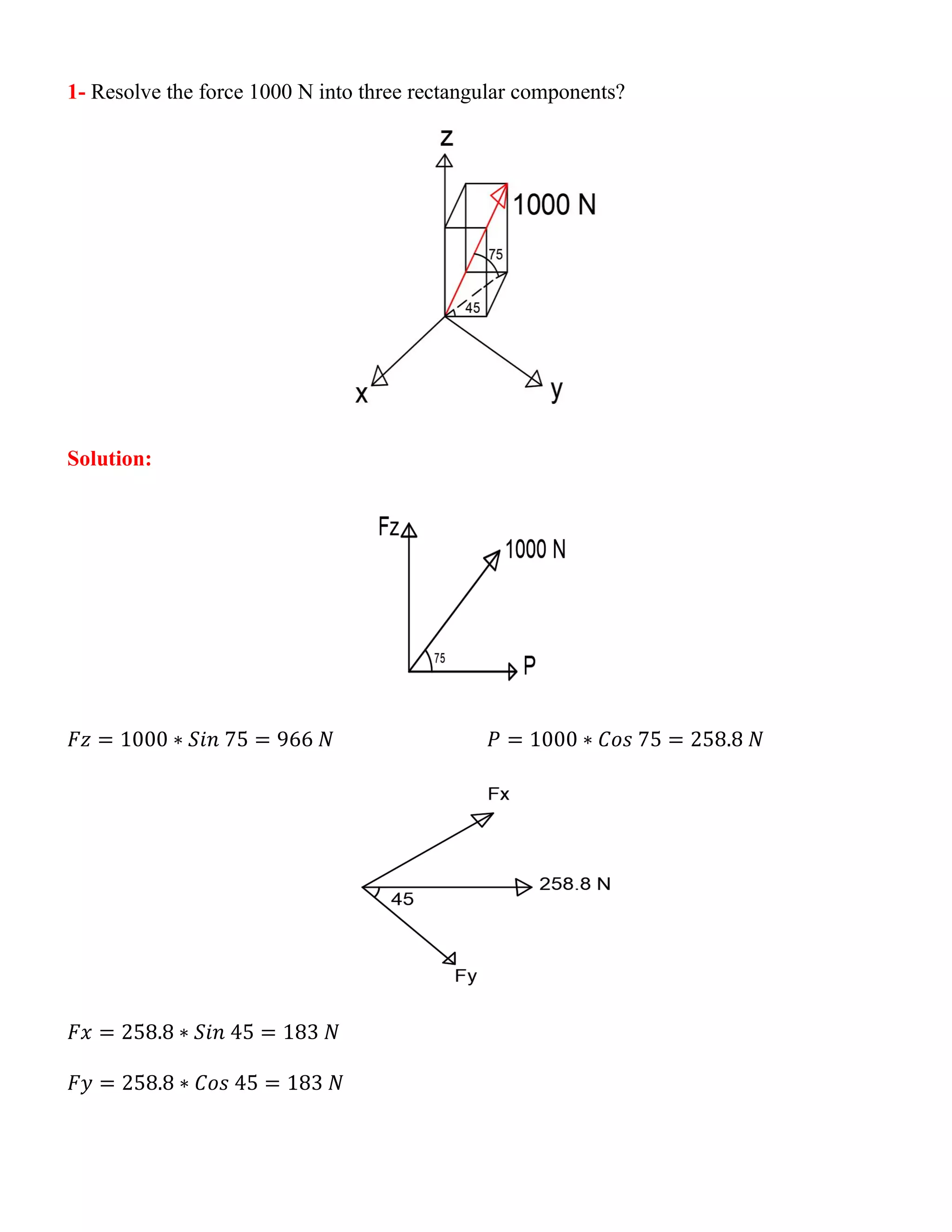
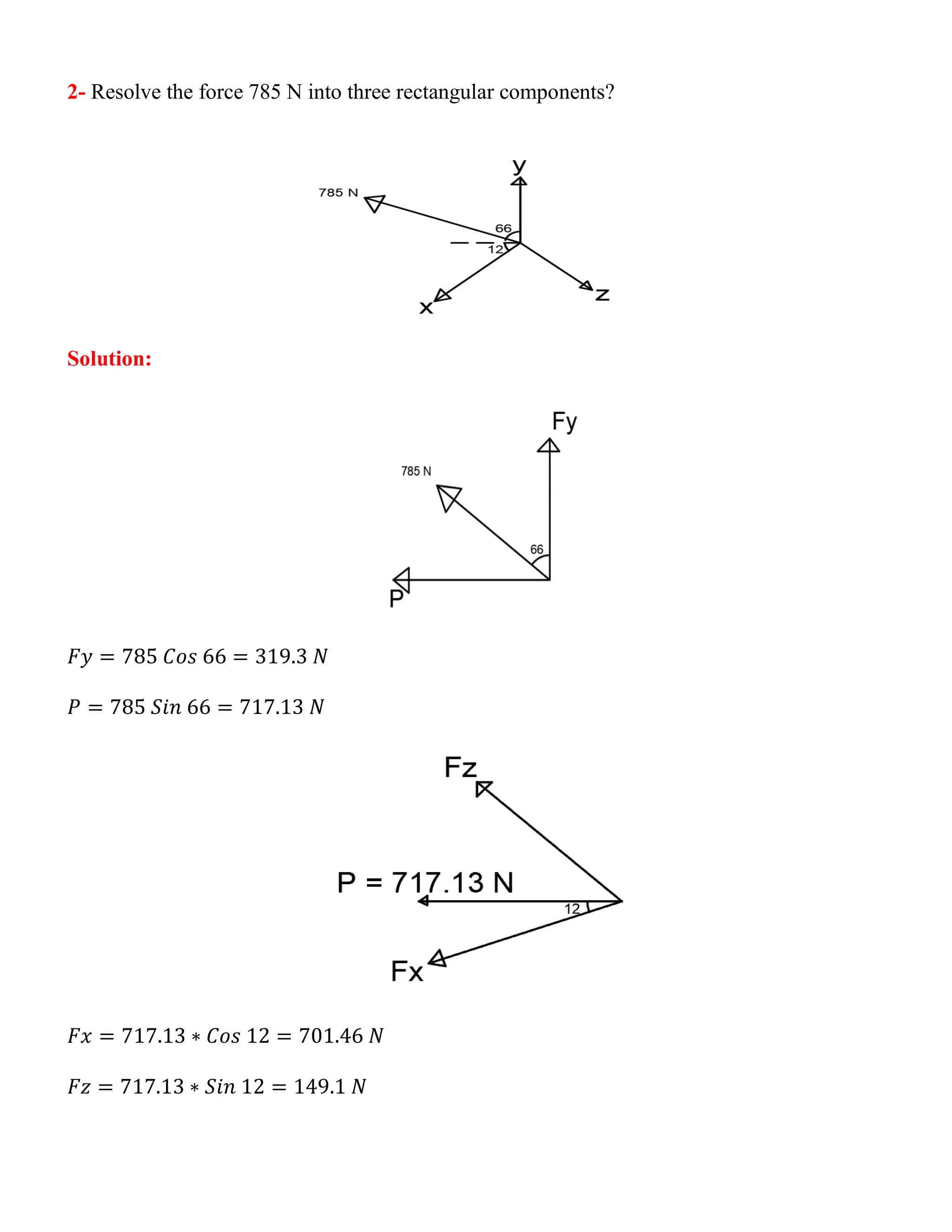
This document provides an introduction to engineering mechanics and statics. It discusses types of loads, force analysis, moments, and force resultants. It also describes how to resolve forces into three rectangular components in three situations: 1) when given the force and coordinate dimensions, 2) when given coordinates and two angles, and 3) when given the starting and ending force coordinates. Examples are provided for resolving forces into x, y, and z components.

1. ENGINEERING MECHANICS
STATCS
For all Engineering Departments
of the First Stage
MOHAMMED KADHIM

2. TABLE OF CONTENTS
UNITS CONVERT …………………………………………….…………….……………...,
INTRODUCTION ABOUT MECHANICS …………………………….…………..………..
TYPES OF LOADS ……………………………………………………….………………….
FORCES ANALYSIS ……………………..………………………………...………………..
MOMENT …………………………………………………………………………………….
FORCES RESULTANT ……………..………………………………………………………..

3. Forces Analysis for Three Dimensions:
(1) When given force within a known coordinate or cube dimension:
‫يع‬ ‫عندما‬
‫ثالثي‬ ‫قوة‬ ‫طي‬
‫األ‬ ‫ة‬
‫مث‬ ‫داخل‬ ‫بعاد‬
‫لث‬
To analyze the forces in three directions, you must find two basic things: the length (L)of the
force direction and scale factor (SF)
:‫مالحظة‬
‫أتج‬
‫دائ‬ ‫المركبات‬ ‫اه‬
‫ما‬
‫ي‬
‫االس‬ ‫من‬ ‫وليس‬ ‫القوة‬ ‫بداية‬ ‫مم‬ ‫حدد‬
‫بأتج‬ ‫تكون‬ ‫المركبات‬ ‫ودائما‬ ‫هم‬
‫ا‬ ‫اه‬
‫المثلث‬ ‫ضالع‬
𝑳 = √(∆𝒙)𝟐 + (∆𝒚)𝟐 + (∆𝒛)𝟐
∆𝒙 = 𝒙𝒇 − 𝒙𝒔 , ∆𝒚 = 𝒚𝒇 − 𝒚𝒔 , ∆𝒛 = 𝒛𝒇 − 𝒛𝒔
𝒙𝒇, 𝒚𝒇, 𝒛𝒇 = ‫قوة‬ ‫نهاية‬ ‫أحداثيات‬
𝒙𝒔, 𝒚𝒔, 𝒚𝒔 = ‫قوة‬ ‫بداية‬ ‫أحداثيات‬
𝑺𝒄𝒂𝒍𝒆 𝑭𝒂𝒄𝒕𝒐𝒓 (𝑺𝑭) =
𝑭
𝑳
𝑭𝒙 = 𝑺𝑭 ∗ ∆𝒙
𝑭𝒚 = 𝑺𝑭 ∗ ∆𝒚
𝑭𝒛 = 𝑺𝑭 ∗ ∆𝒛

4. Examples
1- Determine a rectangular components of the force 400 Ib in the fig blew?
Solution:
𝐿 = √(∆𝑥)2 + (∆𝑦)2 + (∆𝑧)2 → 𝐿 = √72 + 42 + 52 = 9.5𝑓𝑡
𝑆𝐹 =
𝐹
𝐿
=
400
9.5
= 42.105 𝐼𝑏 𝑝𝑒𝑟 𝑓𝑡
𝐹𝑥 = 𝑆𝐹 ∗ ∆𝑥 = 42.105 ∗ 5 = 210.525 𝐼𝑏
𝐹𝑦 = 𝑆𝐹 ∗ ∆𝑦 = 42.105 ∗ 4 = 168.42 𝐼𝑏
𝐹𝑧 = 𝑆𝐹 ∗ ∆𝑧 = 42.105 ∗ 7 = 294.735 𝐼𝑏
2- The tension in the rope attached to the eyebolt in fig is 275 Ib as shown. Determine a three
rectangular component?

5. Solution:
𝐿 = √(∆𝑥)2 + (∆𝑦)2 + (∆𝑧)2 → 𝐿 = √62 + 112 + 82 = 14.87𝑓𝑡
𝑆𝐹 =
𝐹
𝐿
=
275
14.87
= 18.5 𝐼𝑏 𝑝𝑒𝑟 𝑓𝑡
𝐹𝑥 = 𝑆𝐹 ∗ ∆𝑥 = 18.5 ∗ 6 = 111 𝐼𝑏
𝐹𝑦 = 𝑆𝐹 ∗ ∆𝑦 = 18.5 ∗ 11 = 203.5 𝐼𝑏
𝐹𝑧 = 𝑆𝐹 ∗ ∆𝑧 = 18.5 ∗ 8 = 148 𝐼𝑏
(2) When it gives coordinates or cube unknown dimensions and gives two angles:
‫وزاويتين‬ ‫االبعاد‬ ‫معلوم‬ ‫غير‬ ‫مكعب‬ ‫يعطي‬ ‫عندما‬

6. 1- Resolve the force 1000 N into three rectangular components?
Solution:
𝐹𝑧 = 1000 ∗ 𝑆𝑖𝑛 75 = 966 𝑁 𝑃 = 1000 ∗ 𝐶𝑜𝑠 75 = 258.8 𝑁
𝐹𝑥 = 258.8 ∗ 𝑆𝑖𝑛 45 = 183 𝑁
𝐹𝑦 = 258.8 ∗ 𝐶𝑜𝑠 45 = 183 𝑁

7. 2- Resolve the force 785 N into three rectangular components?
Solution:
𝐹𝑦 = 785 𝐶𝑜𝑠 66 = 319.3 𝑁
𝑃 = 785 𝑆𝑖𝑛 66 = 717.13 𝑁
𝐹𝑥 = 717.13 ∗ 𝐶𝑜𝑠 12 = 701.46 𝑁
𝐹𝑧 = 717.13 ∗ 𝑆𝑖𝑛 12 = 149.1 𝑁

8. (3) When a force gives the coordinates of the starting points of the force and the finishing
of the force.
‫واحداثيات‬ ‫قوة‬ ‫يعطي‬ ‫عندما‬
‫القوة‬ ‫نهاية‬ ‫واحداثيات‬ ‫القوة‬ ‫بداية‬
∆𝒙 = 𝒙𝟐 − 𝒙𝟏 ∆𝒚 = 𝒚𝟐 − 𝒚𝟏 ∆𝒛 = 𝒛𝟐 − 𝒛𝟏
𝑳 = √(∆𝒙)𝟐 + (∆𝒚)𝟐 + (∆𝐳)𝟐
𝑺𝑭 =
𝑭
𝑳
𝑭𝒙 = 𝑺𝑭 ∗ ∆𝒙 𝑭𝒚 = 𝑺𝑭 ∗ ∆𝒚 𝑭𝒛 = 𝑺𝑭 ∗ ∆𝒛
Determine the coordinates of points:
1- If the point is located on one of the main axes:
‫كانت‬ ‫اذا‬
‫النقطة‬
‫الرئيسية‬ ‫النقاط‬ ‫احد‬ ‫على‬ ‫تقع‬
𝐴(7, 0, 0) , (𝑥, 0, 0) 𝑎𝑡 𝑥 − 𝑎𝑥𝑠𝑖𝑠
𝐵(0, 3, 0) , (0, 𝑦, 0) 𝑎𝑡 𝑦 − 𝑎𝑥𝑠𝑖𝑠
𝐶(0, 0, 11), (0, 0, 𝑧) 𝑎𝑡 𝑧 − 𝑎𝑥𝑠𝑖𝑠
2- If the point is not located on one of the main axes in this case we depend on the distances.
‫اذا‬
‫واقعه‬ ‫غير‬ ‫النقطة‬ ‫كانت‬
‫الرئ‬ ‫المحاور‬ ‫احد‬ ‫على‬
‫المسافات‬ ‫على‬ ‫نعتمد‬ ‫الحالة‬ ‫هذه‬ ‫في‬ ‫يسية‬
𝐴 (12, 4, 0), 𝐵 (0, 4, 3), 𝐶 (12, 0, 3), 𝐷 (12, 4, 3)

9. Examples:
1- Resolve the force 425 N into three components?
Solution:
𝐵 (6, 4, 0), 𝐶 (7, 6, −2)
∆𝑥 = 7 − 6 = 1 ∆𝑦 = 6 − 4 = 2 ∆𝑧 = −2 − 0 = −2
𝐿 = √(∆𝑥)2 + (∆𝑦)2 + (∆𝑧)2 → 𝐿 = √12 + 22 + (−2)2 → 𝐿 = 3
𝑆𝐹 =
𝐹
𝐿
=
425
3
= 141.67 𝑁
𝐹𝑥 = ∆𝑥 ∗ 𝑆𝐹 = 1 ∗ 141.67 = 141.67 𝑁
𝐹𝑦 = ∆𝑦 ∗ 𝑆𝐹 = 2 ∗ 141.67 = 283.64 𝑁
𝐹𝑧 = ∆𝑧 ∗ 𝑆𝐹 = −2 ∗ 141.67 = −283.34 𝑁

10. 2- Resolve the forces show in the fig 𝐹1 = 125 𝑘𝑁 , 𝐹2 = 235 𝑘𝑁 into three components?
Solution:
For analysis F1
Starting coordinate (0, 1.5, 5) Finishing coordinate (-3, 3.5, 2)
∆𝑥1 = 𝑥𝑓 − 𝑥𝑠 ∆𝑦1 = 𝑦𝑓 − 𝑦𝑠 ∆𝑧1 = 𝑧𝑓 − 𝑧𝑠
∆𝑥1 = −3 − 0 = −3, ∆𝑦1 = 3,5 − 1.5 = 2 , ∆𝑧1 = 2 − 5 = 3
𝐿1 = √(∆𝑥)2 + (∆𝑦)2 + (∆𝑧)2 → 𝐿1 = √(−3)2 + (2)2 + (3)2 → 𝐿 = 4.69𝑚
𝑆𝐹1 =
𝐹1
𝐿1
=
125
4.69
= 26.65
𝐹𝑥1 = 𝑆𝐹1 ∗ ∆𝑋1 = 26.65 ∗ −3 = −79.95 𝑘𝑁
𝐹𝑦1 = 𝑆𝐹1 ∗ ∆𝑦1 = 26.65 ∗ 2 = 53.3 𝑘𝑁
𝐹𝑧1 = 𝑆𝐹1 ∗ ∆𝑧1 = 26.65 ∗ 3 = 79.95 𝑘𝑁
For analysis F2
Starting coordinate (0, 0, 0) Finishing coordinate (2, 1.5, 5)
∆𝑥2 = 𝑥𝑓 − 𝑥𝑠 ∆𝑦2 = 𝑦𝑓 − 𝑦𝑠 ∆𝑧2 = 𝑧𝑓 − 𝑧𝑠

11. ∆𝑥2 = 2 − 0 = 2, ∆𝑦2 = 1.5 − 0 = 1.5, ∆𝑧2 = 5 − 0 = 5
𝐿2 = √(∆𝑥)2 + (∆𝑦)2 + (∆𝑧)2 → 𝐿2 = √22 + 1.52 + 52 = 5.59𝑚
𝑆𝐹2 =
𝐹2
𝐿2
=
235
5.59
= 42.04
𝐹𝑥2 = 𝑆𝐹2 ∗ ∆𝑥2 = 42.04 ∗ 2 = 84.08 𝑘𝑁
𝐹𝑦2 = 𝑆𝐹2 ∗ ∆𝑦2 = 42.04 ∗ 1.5 = 63.06 𝑘𝑁
𝐹𝑧2 = 𝑆𝐹2 ∗ ∆𝑧2 = 42.04 ∗ 5 = 210.2 𝑘𝑁