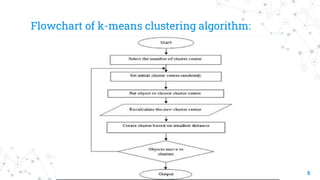
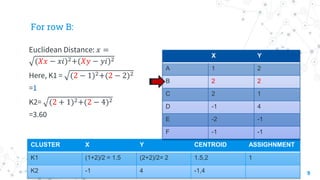
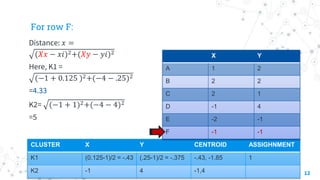
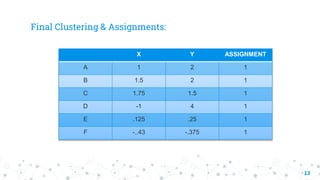
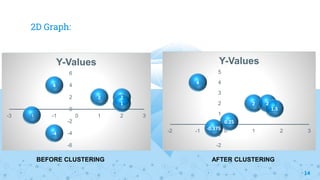
The document explains the k-means clustering algorithm and its implementation steps, highlighting how to categorize a dataset into groups using unsupervised learning. It provides a detailed pseudocode, methodological approach for initial centroids, and iterative calculations for assigning data points to clusters. Additionally, it includes a practical example of performing k-means clustering on a given set of points and visualizing the results on a 2D graph.

1. K-means Clustering:
Algorithm, Evaluation Methods, and Graph

2. Hello!
I am Iffat Firozy
I am here because I love to
teach.
2

3. “
We are given a data set of items, with certain features, and
values for these features (like a vector). The task is to
categorize those items into groups. To achieve this, we will
use the kMeans algorithm; an unsupervised learning
algorithm.
3

4. The above algorithm in pseudocode:
◎ Specify number of clusters K.
◎ Initialize centroids by first shuffling the dataset and then randomly
selecting K data points for the centroids without replacement.
◎ Keep iterating until there is no change to the centroids. i.e
assignment of data points to clusters isn’t changing.
◎ Compute the sum of the squared distance between data points and
all centroids.
◎ Assign each data point to the closest cluster (centroid).
◎ Compute the centroids for the clusters by taking the average of the
all data points that belong to each cluster.
4

5. Flowchart of k-means clustering algorithm:
5

6. LETS’ SOLVE A PROBLEM
6

7. Problem on K-means clustering.
Given are the points A = (1,2), B = (2,2), C = (2, 1), D = (-1, 4), E = (-2, -
1), F = (-1,-1)
a) Starting from initial clusters Cluster1 = {A} which contains only the
point A and Cluster2 = {D} which contains only the point D, run the K-
means clustering algorithm and report the final clusters.
b) Draw the points on a 2-D grid and check if the clusters make
sense.
7

8. Initially:
8
X Y
A 1 2
B 2 2
C 2 1
D -1 4
E -2 -1
F -1 -1
CLUSTER X Y CENTROID ASSIGHNMENT
K1 1 2 1,2 1
K2 -1 4 -1,4 2

9. For row B:
Euclidean Distance: 𝑥 =
(𝑋𝑥 − 𝑥𝑖)2+(𝑋𝑦 − 𝑦𝑖)2
Here, K1 = (2 − 1)2+(2 − 2)2
=1
K2= (2 + 1)2+(2 − 4)2
=3.60
9
CLUSTER X Y CENTROID ASSIGHNMENT
K1 (1+2)/2 = 1.5 (2+2)/2= 2 1.5,2 1
K2 -1 4 -1,4
X Y
A 1 2
B 2 2
C 2 1
D -1 4
E -2 -1
F -1 -1

10. For row C:
Distance: 𝑥 =
(𝑋𝑥 − 𝑥𝑖)2+(𝑋𝑦 − 𝑦𝑖)2
Here, K1 = (2 − 1.5)2+(1 − 2)2
=1.11
K2= (2 + 1)2+(1 − 4)2
=4.24
10
CLUSTER X Y CENTROID ASSIGHNMENT
K1 (1.5+2)/2 = 1.75 (2+1)/2 = 1.5 1.75,1.5 1
K2 -1 4 -1,4
X Y
A 1 2
B 2 2
C 2 1
D -1 4
E -2 -1
F -1 -1

11. For row E:
Distance: 𝑥 =
(𝑋𝑥 − 𝑥𝑖)2+(𝑋𝑦 − 𝑦𝑖)2
Here, K1 =
(−2 − 1.75)2+(−1 − 1.5)2
=4.50
K2= (−2 + 1)2+(−1 − 4)2
=5.09
11
CLUSTER X Y CENTROID ASSIGHNMENT
K1 (1.75-2)/2 = -
0.125
(1.5-1)/2 = 0.25 -0.125, 0.25 1
K2 -1 4 -1,4
X Y
A 1 2
B 2 2
C 2 1
D -1 4
E -2 -1
F -1 -4

12. For row F:
Distance: 𝑥 =
(𝑋𝑥 − 𝑥𝑖)2+(𝑋𝑦 − 𝑦𝑖)2
Here, K1 =
(−1 + 0.125 )2+(−4 − .25)2
=4.33
K2= (−1 + 1)2+(−4 − 4)2
=5
12
CLUSTER X Y CENTROID ASSIGHNMENT
K1 (0.125-1)/2 = -.43 (.25-1)/2 = -.375 -.43, -1.85 1
K2 -1 4 -1,4
X Y
A 1 2
B 2 2
C 2 1
D -1 4
E -2 -1
F -1 -1

13. Final Clustering & Assignments:
13
X Y ASSIGNMENT
A 1 2 1
B 1.5 2 1
C 1.75 1.5 1
D -1 4 1
E .125 .25 1
F -..43 -.375 1

14. 2D Graph:
14
2 2
1
4
-1
-4
-6
-4
-2
0
2
4
6
-3 -2 -1 0 1 2 3
Y-Values
2 2
1.5
4
0.25
-0.375
-2
-1
0
1
2
3
4
5
-2 -1 0 1 2 3
Y-Values
AFTER CLUSTERINGBEFORE CLUSTERING

15. Thanks!
Any questions?
You can find me at:
ifirozy@gmail.com
15