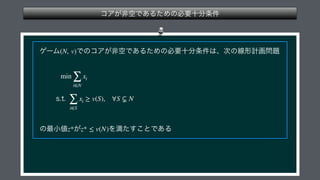
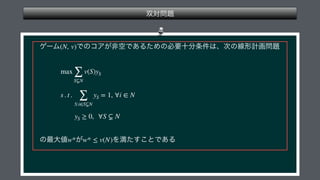
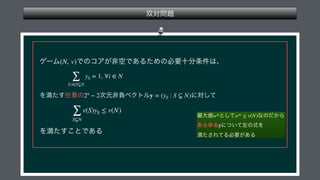
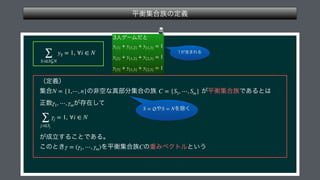
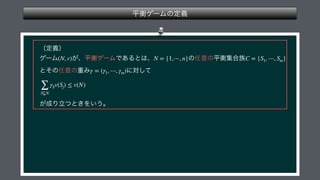
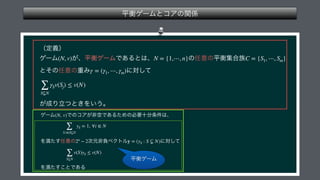
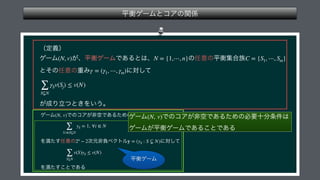
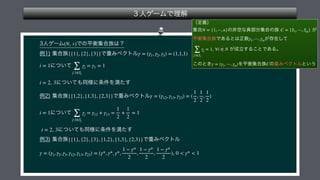
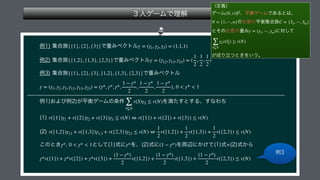
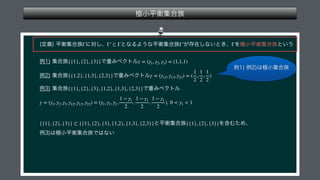
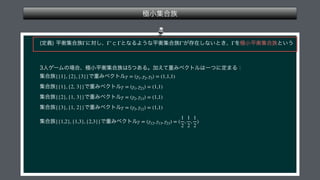
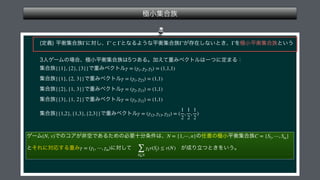
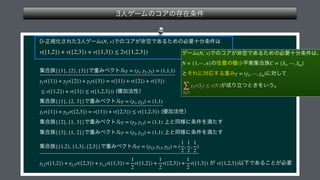
The document presents a mathematical framework addressing value functions and their relationships across various subsets of a set denoted as 'n.' It outlines constraints and conditions for maximizing and minimizing values associated with partitions of subsets using variables like γ and v. The overall emphasis is on the relationship between individual and collective values in the context of possible subsets.

1. 4

2. 1.

3. 1.
(a)
(b)
(c)
(d)
(e)
2.
(a)
(b)
(c)3

5.
(N, v)
min
∑
i∈N
xi
∑
i∈S
xi ≥ v(S), ∀S ⊊ N
z* z* ≤ v(N)

6.
(N, v)
min
∑
i∈N
xi
∑
i∈S
xi ≥ v(S), ∀S ⊊ N
z* z* ≤ v(N)
z*, w*
z* = w*
max
∑
S⊊N
v(S)yS
s . t .
∑
S:i∈S⊊N
yS = 1, ∀i ∈ N
yS ≥ 0, ∀S ⊊ N

7.
(N, v)
max
∑
S⊊N
v(S)yS
s . t .
∑
S:i∈S⊊N
yS = 1, ∀i ∈ N
yS ≥ 0, ∀S ⊊ N
w* w* ≤ v(N)

8.
(N, v)
∑
S:i∈S⊊N
yS = 1, ∀i ∈ N
2n
− 2 y = (yS : S ⊊ N)
∑
S⊊N
v(S)yS ≤ v(N)
w* w* ≤ v(N)
y

9.
∑
S:i∈S⊊N
yS = 1, ∀i ∈ N
N = {1,⋯, n} C = {S1, ⋯, Sm}
γ1, ⋯, γm
∑
j:i∈Sj
γj = 1, ∀i ∈ N
γ = (γ1, ⋯, γm) C
y{1} + y{1,2} + y{1,3} = 1
y{2} + y{1,2} + y{2,3} = 1
y{3} + y{1,3} + y{2,3} = 1
S = ∅ S = N

10.
(N, v) N = {1,⋯, n} C = {S1, ⋯, Sm}
γ = (γ1, ⋯, γm)
∑
S⊊N
γSv(Sj) ≤ v(N)

11.
(N, v) N = {1,⋯, n} C = {S1, ⋯, Sm}
γ = (γ1, ⋯, γm)
∑
S⊊N
γSv(Sj) ≤ v(N)
(N, v)
∑
S:i∈S⊊N
yS = 1, ∀i ∈ N
2n
− 2 y = (yS : S ⊊ N)
∑
S⊊N
v(S)yS ≤ v(N)

12.
(N, v) N = {1,⋯, n} C = {S1, ⋯, Sm}
γ = (γ1, ⋯, γm)
∑
S⊊N
γSv(Sj) ≤ v(N)
(N, v)
∑
S:i∈S⊊N
yS = 1, ∀i ∈ N
2n
− 2 y = (yS : S ⊊ N)
∑
S⊊N
v(S)yS ≤ v(N)
(N, v)

13. 3

14.
(N, v)
{{1}, {2}, {3}} γ = (γ1, γ2, γ3) = (1,1,1)
i = 1
∑
j:1∈Sj
γj = γ1 = 1
i = 2, 3
{{1,2}, {1,3}, {2,3}} γ = (γ12, γ13, γ23) = (
1
2
,
1
2
,
1
2
)
i = 1
∑
j:1∈Sj
γj = γ12 + γ13 =
1
2
+
1
2
= 1
i = 2, 3
{{1}, {2}, {3}, {1,2}, {1,3}, {2,3}}
γ = (γ1, γ2, γ3, γ12, γ13, γ23) = (γ*, γ*, γ*,
1 − γ*
2
,
1 − γ*
2
,
1 − γ*
2
) 0 < γ* < 1
N = {1,⋯, n} C = {S1, ⋯, Sm}
γ1, ⋯, γm
∑
j:i∈Sj
γj = 1, ∀i ∈ N
γ = (γ1, ⋯, γm) C

15.
{{1}, {2}, {3}} γ = (γ1, γ2, γ3) = (1,1,1)
{{1,2}, {1,3}, {2,3}} γ = (γ12, γ13, γ23) = (
1
2
,
1
2
,
1
2
)
{{1}, {2}, {3}, {1,2}, {1,3}, {2,3}}
γ = (γ1, γ2, γ3, γ12, γ13, γ23) = (γ*, γ*, γ*,
1 − γ*
2
,
1 − γ*
2
,
1 − γ*
2
) 0 < γ* < 1
∑
S⊊N
v(S)γS ≤ v(N)
v({1})γ1 + v({2})γ2 + v({3})γ3 ≤ v(N) ⇔ v({1}) + v({2}) + v({3}) ≤ v(N)
v({1,2})γ12 + v({1,3})γ1,3 + v({2,3})γ23 ≤ v(N) ⇔
1
2
v({1,2}) +
1
2
v({1,3}) +
1
2
v({2,3}) ≤ v(N)
γ* 0 < γ* < 1 γ* (1 − γ*)
γ*v({1}) + γ*v({2}) + γ*v({3}) +
(1 − γ*)
2
v({1,2}) +
(1 − γ*)
2
v({1,3}) +
(1 − γ*)
2
v({2,3}) ≤ v(N)
(N, v)
N = {1,⋯, n} C = {S1, ⋯, Sm}
γ = (γ1, ⋯, γm)
∑
S⊊N
γSv(Sj) ≤ v(N)

16.
Γ Γ′ ⊂ Γ Γ′ Γ
{{1}, {2}, {3}} γ = (γ1, γ2, γ3) = (1,1,1)
{{1,2}, {1,3}, {2,3}} γ = (γ12, γ13, γ23) = (
1
2
,
1
2
,
1
2
)
{{1}, {2}, {3}, {1,2}, {1,3}, {2,3}}
γ = (γ1, γ2, γ3, γ12, γ13, γ23) = (γ1, γ1, γ1,
1 − γ1
2
,
1 − γ1
2
,
1 − γ1
2
) 0 < γ1 < 1
{{1}, {2}, {3}} ⊂ {{1}, {2}, {3}, {1,2}, {1,3}, {2,3}} {{1}, {2}, {3}}

17.
Γ Γ′ ⊂ Γ Γ′ Γ
{{1}, {2}, {3}} γ = (γ1, γ2, γ3) = (1,1,1)
{{1}, {2, 3}} γ = (γ1, γ23) = (1,1)
{{2}, {1, 3}} γ = (γ2, γ13) = (1,1)
{{3}, {1, 2}} γ = (γ3, γ12) = (1,1)
{{1,2}, {1,3}, {2,3}} γ = (γ12, γ13, γ23) = (
1
2
,
1
2
,
1
2
)

18.
Γ Γ′ ⊂ Γ Γ′ Γ
{{1}, {2}, {3}} γ = (γ1, γ2, γ3) = (1,1,1)
{{1}, {2, 3}} γ = (γ1, γ23) = (1,1)
{{2}, {1, 3}} γ = (γ2, γ13) = (1,1)
{{3}, {1, 2}} γ = (γ3, γ12) = (1,1)
{{1,2}, {1,3}, {2,3}} γ = (γ12, γ13, γ23) = (
1
2
,
1
2
,
1
2
)
(N, v) N = {1,⋯, n} C = {S1, ⋯, Sm}
γ = (γ1, ⋯, γm)
∑
S⊊N
γSv(Sj) ≤ v(N)

19.
(N, v)
v({1,2}) + v({2,3}) + v({1,3}) ≤ 2v({1,2,3})
{{1}, {2}, {3}} γ = (γ1, γ2, γ3) = (1,1,1)
γ1v({1}) + γ2v({2}) + γ3v({3}) = v({1}) + v({2}) + v({3})
≤ v({1,2}) + v({3}) ≤ v({1,2,3}))
{{1}, {2, 3}} γ = (γ1, γ23) = (1,1)
γ1v({1}) + γ23v({2,3}) = v({1}) + v({2,3}) ≤ v({1,2,3})
{{2}, {1, 3}} γ = (γ2, γ13) = (1,1)
{{3}, {1, 2}} γ = (γ3, γ12) = (1,1)
{{1,2}, {1,3}, {2,3}} γ = (γ12, γ13, γ23) = (
1
2
,
1
2
,
1
2
)
γ12v({1,2}) + γ2,3v({2,3}) + γ1,3v({1,3}) =
1
2
v({1,2}) +
1
2
v({2,3}) +
1
2
v({1,3}) v({1,2,3})
(N, v)
N = {1,⋯, n} C = {S1, ⋯, Sm}
γ = (γ1, ⋯, γm)
∑
S⊊N
γSv(Sj) ≤ v(N)

21. See you next time