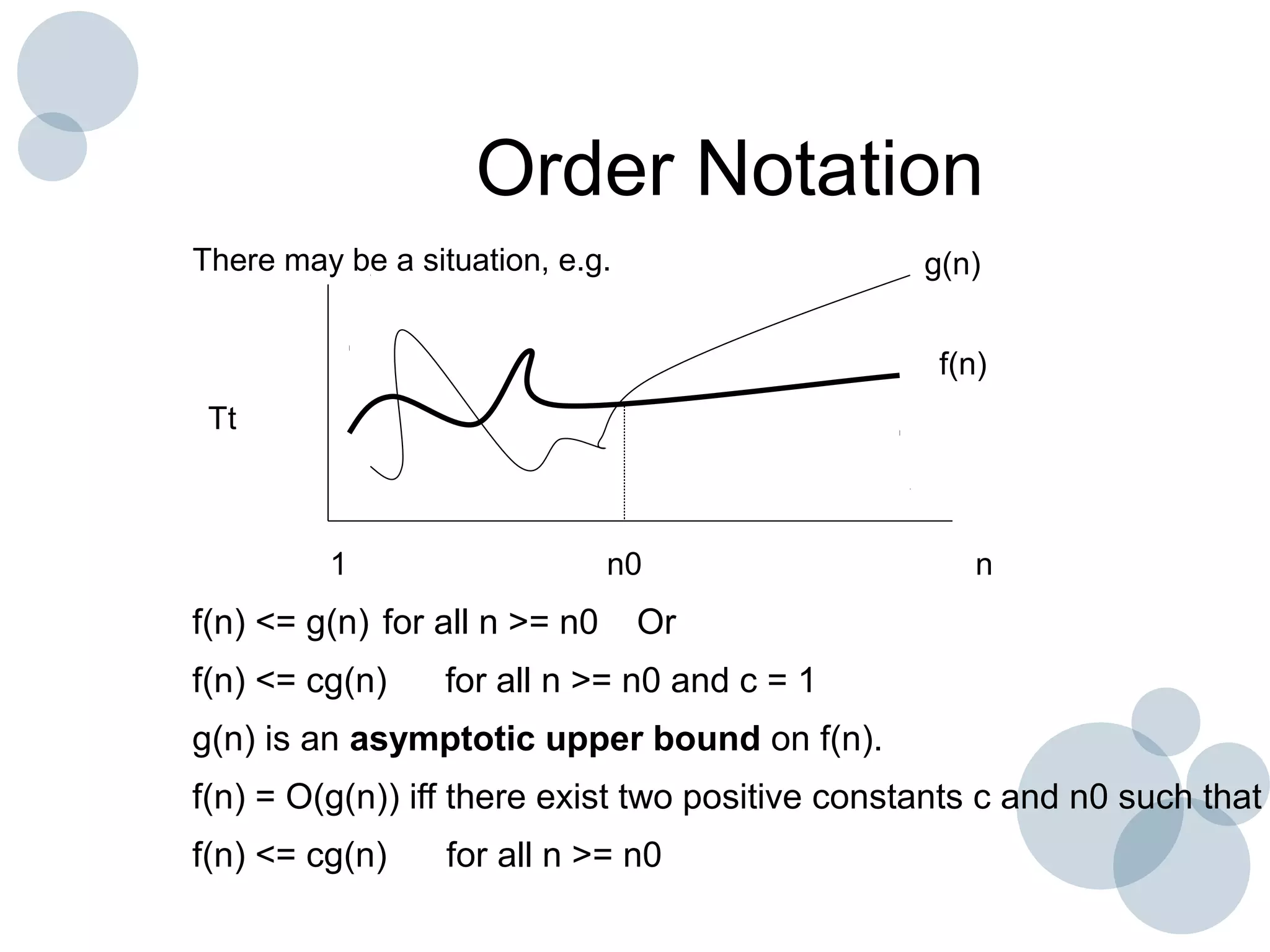
Time complexity analysis specifies how the running time of an algorithm depends on the size of its input. It is determined by identifying the basic operation of the algorithm and counting how many times it is executed as the input size increases. The time complexity of an algorithm can be expressed as a function T(n) relating the input size n to the running time. Common time complexities include constant O(1), linear O(n), logarithmic O(log n), and quadratic O(n^2). The order of growth indicates how fast the running time grows as n increases and is used to compare the efficiency of algorithms.

1. Time Complexity &
Order Of Growth
Analysis of Algorithm

2. • Efficiency of Algorithms
– Space Complexity
– Determination of the s[ace used by algorithm other
than its input size is known as space complexity
Analysis
– Time Complexity

3. The Time Complexity of an
Algorithm
Specifies how the running time depends
on the size of the input
3

4. Purpose

5. Purpose
• To estimate how long a program will run.
• To estimate the largest input that can reasonably be
given to the program.
• To compare the efficiency of different algorithms.
• To help focus on the parts of code that are executed
the largest number of times.
• To choose an algorithm for an application.

6. Purpose (Example)
• Suppose a machine that performs a million
floating-point operations per second (106 FLOPS),
then how long an algorithm will run for an input of
size n=50?
– 1) If the algorithm requires n2 such operations:

7. Purpose (Example)
• Suppose a machine that performs a million
floating-point operations per second (106 FLOPS),
then how long an algorithm will run for an input of
size n=50?
– 1) If the algorithm requires n2 such operations:
– 0.0025 second

8. Purpose (Example)
• Suppose a machine that performs a million floating-
point operations per second (106 FLOPS), then
how long an algorithm will run for an input of size
n=50?
– 1) If the algorithm requires n2 such operations:
– 0.0025 second
– 2) If the algorithm requires 2n such operations:
– A) Takes a similar amount of time (t < 1 sec)
– B) Takes a little bit longer time (1 sec < t < 1 year)
– C) Takes a much longer time (1 year < t)

9. Purpose (Example)
• Suppose a machine that performs a million
floating-point operations per second (106 FLOPS),
then how long an algorithm will run for an input of
size n=50?
– 1) If the algorithm requires n2 such operations:
– 0.0025 second
– 2) If the algorithm requires 2n such operations:
– over 35 years!

10. Time Complexity Is a Function
Specifies how the running time depends on
the size of the input.
A function mapping
“size” of input
“time” T(n) executed .

11. Definition of Time?

12. Definition of Time
• # of seconds (machine, implementation
dependent).
• # lines of code executed.
• # of times a specific operation is
performed (e.g., addition).

13. Theoretical analysis of time
efficiencyTime efficiency is analyzed by determining
the number of repetitions of the basic
operation as a function of input size
• Basic operation: the operation that
contributes most towards the running time
of the algorithm.
●
●
T(n) ≈ copC(n)
running time
execution time
for basic operation
Number of times
basic operation is
executed
input size

14. Input size and basic operation
examples
Problem Input size measure Basic operation
Search for key in a list of
n items
Multiply two matrices of
floating point numbers
Compute an
Graph problem

15. Input size and basic operation
examples
Problem Input size measure Basic operation
Search for key in a list of
n items
Number of items in the
list: n
Key comparison
Multiply two matrices of
floating point numbers
Compute an
Graph problem

16. Input size and basic operation
examples
Problem Input size measure Basic operation
Search for key in a list of
n items
Number of items in the
list: n
Key comparison
Multiply two matrices of
floating point numbers
Dimensions of matrices
Floating point
multiplication
Compute an
Graph problem

17. Input size and basic operation
examples
Problem Input size measure Basic operation
Search for key in list of
n items
Number of items in list n Key comparison
Multiply two matrices of
floating point numbers
Dimensions of matrices
Floating point
multiplication
Compute an n
Floating point
multiplication
Graph problem

18. Input size and basic operation
examples
Problem Input size measure Basic operation
Search for key in list of
n items
Number of items in list n Key comparison
Multiply two matrices of
floating point numbers
Dimensions of matrices
Floating point
multiplication
Compute an n
Floating point
multiplication
Graph problem #vertices and/or edges
Visiting a vertex or
traversing an edge

19. Time
Complexity
Every Case
Time
Complexity
Not Every
Case
Best Case
Worst Case
Average Case
Time Complexity

20. Every case Time Complexity
• For a given algorithm, T(n) is every case
time complexity if algorithm have to repeat
its basic operation every time for given
input size n. determination of T(n) is called
every case time complexity analysis.

21. Every case time
Complexity(examples)
• Sum of elements of array
Algorithm sum_array(A,n)
sum=0
for i=1 to n
sum+=A[i]
return sum

22. Every case time
Complexity(examples)
• Basic operation sum(adding up elements
of array
• Repeated how many number of times??
– For every element of array
• Complexity T(n)=O(n)

23. Every case time
Complexity(examples)
• Exchange Sort
Algorithm exchange_sort(A,n)
for i=1 to n-1
for j= i+1 to n
if A[i]>A[j]
exchange A[i] &A[j]

24. • Basic operation comparison of array
elements
• Repeated how many number of times??
• Complexity T(n)=n(n-1)/2=O(n^2)

25. Best Case Time Complexity
• For a given algorithm, B(n) is best case
time complexity if algorithm have to repeat
its basic operation for minimum time for
given input size n. determination of B(n) is
called Best case time complexity analysis.

26. Best Case Time Complexity
(Example)
Algorithm sequential_search(A,n,key)
i=0
while i<n && A[i]!= key
i=i+1
If i<n
return i
Else return-1

27. • Input size: number of elements in the
array i.e. n
• Basic operation :comparison of key with
array elements
• Best case: first element is the required key

28. Worst Case Time Complexity
• For a given algorithm, W(n) is worst case
time complexity if algorithm have to repeat
its basic operation for maximum number
of times for given input size n.
determination of W(n) is called worst case
time complexity analysis.

29. Sequential Search
• Input size: number of elements in the
array i.e. n
• Basic operation :comparison of key with
array elements
• worst case: last element is the required
key or key is not present in array at all
• Complexity :w(n)=O(n)

30. Average Case Time Complexity
• For a given algorithm, A(n) is average
case time complexity if algorithm have to
repeat its basic operation for average
number of times for given input size n.
determination of A(n) is called average
case time complexity analysis.

31. • Input size: number of elements in the
array i.e. n
• Basic operation :comparison of key with
array elements

32. • Average case: probability of successful
search is p(0<=p<=1)
• Probability of each element is p/n
multiplied with number of comparisons ie
• p/n*i
• A(n)=[1.p/n+2.p/n+…..n.p/n]+n.(1-p)
p/n(1+2+3+…+n)+n.(1-p)
P(n+1)/2 +n(1-p)

33. What is the order of growth?
In the running time expression, when n becomes large a term will
become significantly larger than the other ones:
this is the so-called dominant term
T1(n)=an+b
T2(n)=a log n+b
T3(n)=a n2+bn+c
T4(n)=an+b n +c
(a>1)
Dominant term: a n
Dominant term: a log n
Dominant term: a n2
Dominant term: an

34. What is the order of growth?
Order of growth
Linear
Logarithmic
Quadratic
Exponential
T’1(kn)= a kn=k T1(n)
T’2(kn)=a log(kn)=T2(n)+alog k
T’3(kn)=a (kn)2=k2 T3(n)
T’4(n)=akn=(an)k

35. How can be interpreted the order of growth?
• Between two algorithms it is considered that the one
having a smaller order of growth is more efficient
• However, this is true only for large enough input sizes
Example. Let us consider
T1(n)=10n+10 (linear order of growth)
T2(n)=n2 (quadratic order of growth)
If n<=10 then T1(n)>T2(n)
Thus the order of growth is relevant only for n>10

36. Growth Rate
0
50
100
150
200
250
300
FunctionValue
Data Size
Growth Rate of Diferent Functions
lg n
n lg n
n square
n cube
2 raise to
power n

37. Growth Rates
n lgn nlgn n2
n3
2n
0 #NUM! #NUM! 0 0 1
1 0 0 1 1 2
2 1 2 4 8 4
4 2 8 16 64 16
8 3 24 64 512 256
16 4 64 256 4096 65536
32 5 160 1024 32768 4.29E+09
64 6 384 4096 262144 1.84E+19
128 7 896 16384 2097152 3.4E+38
256 8 2048 65536 16777216 1.16E+77
512 9 4608 262144 1.34E+08 1.3E+154
1024 10 10240 1048576 1.07E+09
2048 11 22528 4194304 8.59E+09

38. Constant Factors
• The growth rate is not affected by
– constant factors or
– lower-order terms
• Examples
– 102n + 105 is a linear function
– 105n2 + 108n is a quadratic function

39. Asymptotic Notations

40. Order Notation
There may be a situation, e.g.
Tt
1 n
g(n)
f(n)
n0
f(n) <= g(n) for all n >= n0 Or
f(n) <= cg(n) for all n >= n0 and c = 1
g(n) is an asymptotic upper bound on f(n).
f(n) = O(g(n)) iff there exist two positive constants c and n0 such that
f(n) <= cg(n) for all n >= n0

41. Big –O Examples
choice of constant is not unique, for each different value of c there is
corresponding value of no that satisfies basic relationship.

42. Big-O Example

43. More Big-Oh Examples
7n-2
7n-2 is O(n)
need c > 0 and n0 ≥ 1 such that 7n-2 ≤ c•n for n ≥ n0
this is true for c = 7 and n0 = 1
 3n3 + 20n2 + 5
3n3 + 20n2 + 5 is O(n3)
need c > 0 and n0 ≥ 1 such that 3n3 + 20n2 + 5 ≤ c•n3 for n ≥ n0
this is true for c = 28 and n0 = 1
 3 log n + log log n
3 log n + log log n is O(log n)
need c > 0 and n0 ≥ 1 such that 3 log n + log log n ≤ c•log n for n ≥ n0
this is true for c = 4 and n0 = 2

44. Big-Oh and Growth Rate
• The big-Oh notation gives an upper bound on the
growth rate of a function
• The statement “f(n) is O(g(n))” means that the growth
rate of f(n) is no more than the growth rate of g(n)
• We can use the big-Oh notation to rank functions
according to their growth rate
f(n) is O(g(n)) g(n) is O(f(n))
g(n) grows more Yes No
f(n) grows more No Yes
Same growth Yes Yes

45. Big-Oh Example
• Example: the function
n2 is not O(n)
– n2 ≤ cn
– n ≤ c
– The above inequality
cannot be satisfied
since c must be a
constant
1
10
100
1,000
10,000
100,000
1,000,000
1 10 100 1,000
n
n^ 2 100n
10n n

46. Big-Oh Rules
• If is f(n) a polynomial of degree d, then f(n) is
O(nd), i.e.,
1.Drop lower-order terms
2.Drop constant factors
• Use the smallest possible class of functions
–.Say “2n is O(n)” instead of “2n is O(n2)”
• Use the simplest expression of the class
–.Say “3n + 5 is O(n)” instead of “3n + 5 is O(3n)”

47. Order Notation
Asymptotic Lower Bound:f(n) = Ω(g(n)),
iff there exit positive constants c and n0 such that
f(n) >= cg(n) for all n >= n0
nn0
f(n)
g(n)

48. Big Ω Examples

49. Big Ω Examples

50. Big-Omega Notation
• Given functions f(n) and g(n), we say that f(n) is
Ω(g(n)) if there are positive constants
c and n0 such that
f(n) >=cg(n) for n ≥ n0
• Example:
, let c=1/12, n=1

51. Order Notation
Asymptotically Tight Bound: f(n) = θ(g(n)),
iff there exit positive constants c1 and c2 and n0 such that
c1 g(n) <= f(n) <= c2g(n) for all n >= n0
nn0
c2g(n)
c1g(n)
f(n)
This means that the best and worst case requires the same
amount of time to within a constant factor.

52. Θ -Examples

53. Intuition for Asymptotic
Notation
Big-Oh
f(n) is O(g(n)) if f(n) is asymptotically less than or equal to g(n)
big-Omega
f(n) is Ω(g(n)) if f(n) is asymptotically greater than or equal to g(n)
big-Theta
f(n) is Θ(g(n)) if f(n) is asymptotically equal to g(n)

54. Small ‘o’ Notation:
For every c and n if f(n) is always less than g(n) then f(n) belongs to o(g(n)).
Small Omega Notation:
For every c and n if f(n) is always above than g(n) then f(n) belongs to small
omega(g(n)).
Relatives of Big-O

55. Using Limits for Comparing
Order of Growth

56. Small-O Examples

57. Small-Ω

58. Big-O

59. Big-Ω

60. Θ Examples