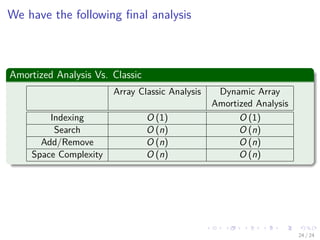
The document discusses the implementation of linear lists using array representation, outlining operations like adding and getting elements, and addressing dynamic resizing of arrays. It explains how to handle array limits by creating larger arrays and copying existing elements, along with a strategy of doubling the size to optimize performance. Space complexity related to dynamic arrays is also examined, detailing trade-offs between time and space efficiency in various programming languages.


![Images/cinvestav-
How do we implement the ADT List?
In our first representation will use an array
Use a one-dimensional array element[]:
a b c d e - - - -
0 1 2 3 4 5 6 7 8
The previous array
A representation of L = (a, b, c, d, e) using position i in element[i].
3 / 24](https://image.slidesharecdn.com/04arraylinearlist-150622141102-lva1-app6891/85/Preparation-Data-Structures-04-array-linear_list-3-320.jpg)
![Images/cinvestav-
How do we implement the ADT List?
In our first representation will use an array
Use a one-dimensional array element[]:
a b c d e - - - -
0 1 2 3 4 5 6 7 8
The previous array
A representation of L = (a, b, c, d, e) using position i in element[i].
3 / 24](https://image.slidesharecdn.com/04arraylinearlist-150622141102-lva1-app6891/85/Preparation-Data-Structures-04-array-linear_list-4-320.jpg)


![Images/cinvestav-
Representation Used In Text
Something Notable
a b c d e - - - -
0 1 2 3 4 5 6 7 8
Size=5
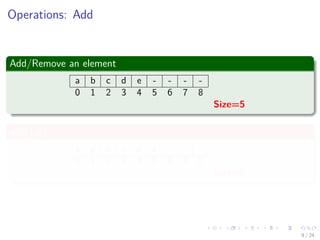
Thus
1 Put element i of list in element[i].
2 Use a variable size to record current number of elements
5 / 24](https://image.slidesharecdn.com/04arraylinearlist-150622141102-lva1-app6891/85/Preparation-Data-Structures-04-array-linear_list-8-320.jpg)
![Images/cinvestav-
Representation Used In Text
Something Notable
a b c d e - - - -
0 1 2 3 4 5 6 7 8
Size=5
Thus
1 Put element i of list in element[i].
2 Use a variable size to record current number of elements
5 / 24](https://image.slidesharecdn.com/04arraylinearlist-150622141102-lva1-app6891/85/Preparation-Data-Structures-04-array-linear_list-9-320.jpg)
![Images/cinvestav-
Code
Our Implementation
p u b l i c c l a s s S i m p l e A r r a y L i s t <Item> implements
L i n e a r L i s t <Item >{
// p r i v a t e elements of implementation
p r o t e c t e d Item element [ ] ;
p r o t e c t e d i n t s i z e ;
p r o t e c t e d f i n a l s t a t i c i n t DEFAULT_SIZE = 10;
// C o n s t r u c t o r s
p u b l i c S i m p l e A r r a y L i s t (){
t h i s . s i z e = 0;
t h i s . element = ( Item [ ] ) new Object [ t h i s . DEFAULT_SIZE ] ;
}
p u b l i c S i m p l e A r r a y L i s t ( i n t NewSize ){
t h i s . s i z e = 0;
t h i s . element = ( Item [ ] ) new Object [ NewSize ] ;
}
6 / 24](https://image.slidesharecdn.com/04arraylinearlist-150622141102-lva1-app6891/85/Preparation-Data-Structures-04-array-linear_list-10-320.jpg)
![Images/cinvestav-
Data Type Of Array element[]
First than anything
Data type of list elements is unknown.
Thus, we used the genericity of Object
1 Then, we use element[] to be of data type Object.
2 Then, we cast to the new “Item.”
However
You cannot put elements of primitive data types (int, float, double, char,
etc.) into our linear lists.
7 / 24](https://image.slidesharecdn.com/04arraylinearlist-150622141102-lva1-app6891/85/Preparation-Data-Structures-04-array-linear_list-11-320.jpg)
![Images/cinvestav-
Data Type Of Array element[]
First than anything
Data type of list elements is unknown.
Thus, we used the genericity of Object
1 Then, we use element[] to be of data type Object.
2 Then, we cast to the new “Item.”
However
You cannot put elements of primitive data types (int, float, double, char,
etc.) into our linear lists.
7 / 24](https://image.slidesharecdn.com/04arraylinearlist-150622141102-lva1-app6891/85/Preparation-Data-Structures-04-array-linear_list-12-320.jpg)
![Images/cinvestav-
Data Type Of Array element[]
First than anything
Data type of list elements is unknown.
Thus, we used the genericity of Object
1 Then, we use element[] to be of data type Object.
2 Then, we cast to the new “Item.”
However
You cannot put elements of primitive data types (int, float, double, char,
etc.) into our linear lists.
7 / 24](https://image.slidesharecdn.com/04arraylinearlist-150622141102-lva1-app6891/85/Preparation-Data-Structures-04-array-linear_list-13-320.jpg)
![Images/cinvestav-
Data Type Of Array element[]
First than anything
Data type of list elements is unknown.
Thus, we used the genericity of Object
1 Then, we use element[] to be of data type Object.
2 Then, we cast to the new “Item.”
However
You cannot put elements of primitive data types (int, float, double, char,
etc.) into our linear lists.
7 / 24](https://image.slidesharecdn.com/04arraylinearlist-150622141102-lva1-app6891/85/Preparation-Data-Structures-04-array-linear_list-14-320.jpg)


![Images/cinvestav-
Code
Our Implementation
p u b l i c void add ( i n t index , Item myobject ){
// I n i t i a l V a r i a b l e s
i n t i ;
// Always check f o r p o s s i b l e e r r o r s
i f ( t h i s . s i z e == element . len ght ){
System . out . p r i n t l n ( " L i s t ␣ does ␣ not ␣ have ␣ space " ) ;
System . e x i t ( 0 ) ;
}
i f ( index <0 | | index >t h i s . s i z e ){
System . out . p r i n t l n ( " Index ␣ out ␣ of ␣bound " ) ;
System . e x i t ( 0 ) ;
}
// S h i f t p o s t i i o n s as n e c e s s a r y
f o r ( i = t h i s . s i z e ; i >index ; i −−)
element [ i +1]=element [ i ] ;
// copy element i n t o c o n t a i n e r
element [ i +1]=myobject ;
}
10 / 24](https://image.slidesharecdn.com/04arraylinearlist-150622141102-lva1-app6891/85/Preparation-Data-Structures-04-array-linear_list-18-320.jpg)
![Images/cinvestav-
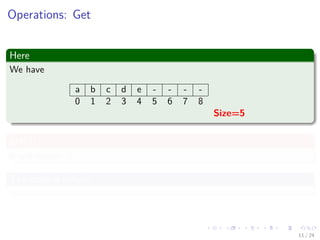
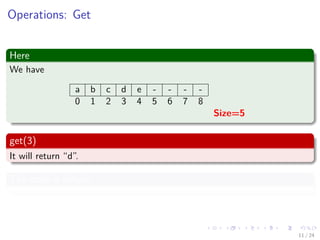
Operations: Get
Here
We have
a b c d e - - - -
0 1 2 3 4 5 6 7 8
Size=5
get(3)
It will return “d”.
The code is simple
p u b l i c Item get ( i n t index ){
// Check always
i f ( t h i s . s i z e == 0) r e t u r n n u l l ;
i f ( index <0 | | index >t h i s . s i z e −1){
System . out . p r i n t l n ( " Index ␣ out ␣ of ␣bound " ) ;
System . e x i t ( 0 ) ;
}
r e t u r n element [ index ]
}
11 / 24](https://image.slidesharecdn.com/04arraylinearlist-150622141102-lva1-app6891/85/Preparation-Data-Structures-04-array-linear_list-21-320.jpg)


![Images/cinvestav-
Example
Example
Length of array element[] is 6:
a b c d e f
First create a new and larger array
NewArray = (Item[]) new Object[12]
- - - - - - - - - - - -
Now copy the new elements into the new array!!!
System.arraycopy(element, 0, newArray, 0, element.length);
a b c d e f - - - - - -
14 / 24](https://image.slidesharecdn.com/04arraylinearlist-150622141102-lva1-app6891/85/Preparation-Data-Structures-04-array-linear_list-25-320.jpg)
![Images/cinvestav-
Example
Example
Length of array element[] is 6:
a b c d e f
First create a new and larger array
NewArray = (Item[]) new Object[12]
- - - - - - - - - - - -
Now copy the new elements into the new array!!!
System.arraycopy(element, 0, newArray, 0, element.length);
a b c d e f - - - - - -
14 / 24](https://image.slidesharecdn.com/04arraylinearlist-150622141102-lva1-app6891/85/Preparation-Data-Structures-04-array-linear_list-26-320.jpg)
![Images/cinvestav-
Example
Example
Length of array element[] is 6:
a b c d e f
First create a new and larger array
NewArray = (Item[]) new Object[12]
- - - - - - - - - - - -
Now copy the new elements into the new array!!!
System.arraycopy(element, 0, newArray, 0, element.length);
a b c d e f - - - - - -
14 / 24](https://image.slidesharecdn.com/04arraylinearlist-150622141102-lva1-app6891/85/Preparation-Data-Structures-04-array-linear_list-27-320.jpg)
![Images/cinvestav-
Example
Finally, rename new array
element = NewArray;
element[0]−→ a b c d e f - - - - - -
15 / 24](https://image.slidesharecdn.com/04arraylinearlist-150622141102-lva1-app6891/85/Preparation-Data-Structures-04-array-linear_list-28-320.jpg)






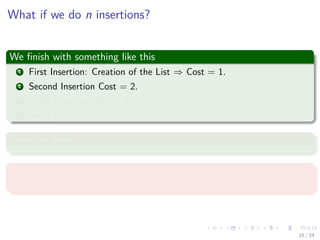

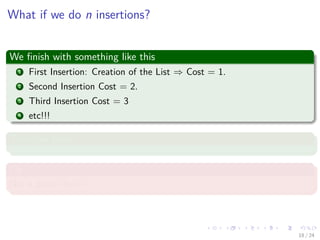



![Images/cinvestav-
A better strategy
Dynamic Array
To avoid incurring the cost of resizing many times, dynamic arrays resize
by an amount a.
In our example we double the size, a = 2
Item NewArray [ ] ;
i f ( t h i s . s i z e == element . len ght ){
// Resize the c a p a c i t y
NewArray = ( Item [ ] ) new Object [ 2*this.size ]
f o r ( i n t i =0; i < s i z e ; i ++){
NewArray [ i ]= element [ i ] ;
}
element = NewArray ;
}
20 / 24](https://image.slidesharecdn.com/04arraylinearlist-150622141102-lva1-app6891/85/Preparation-Data-Structures-04-array-linear_list-43-320.jpg)