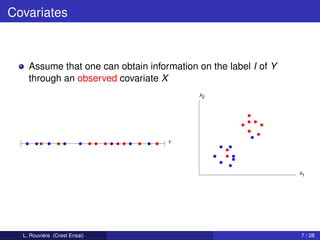
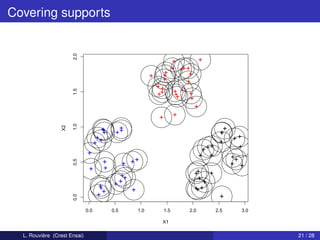
This document describes a clustering procedure and nonparametric mixture estimation. It introduces a mixture density model where the goal is to efficiently estimate the mixture weights (αi) and component densities (fi). A two-stage clustering algorithm is proposed: 1) perform clustering on covariates (X) to estimate labels (Ik), and 2) estimate component densities (fi) using kernel density estimation within each cluster. The performance of this approach depends on the clustering method's misclassification error. A toy example with two components having disjoint support densities for X is provided to illustrate the model.

1. On clustering procedure and nonparametric mixture
estimation
S. Auray, N. Klutchnikoff and L. Rouvière
Crest-Ensai
J ANUARY 2013
L. Rouvière (Crest Ensai) 1 / 28

2. Outline
1 Introduction
2 The model
Notations and examples
Main results
3 Clustering methods
A toy example
Disjoint support densities
L. Rouvière (Crest Ensai) 2 / 28

3. 1 Introduction
2 The model
Notations and examples
Main results
3 Clustering methods
A toy example
Disjoint support densities
L. Rouvière (Crest Ensai) 3 / 28

4. Mixture density model
Let Y be a real random variable drawn from a mixture density
model
M
f (x) = αi fi (x).
i=1
The number of components M is known.
The problem
Find efficient estimators αi and ˆi of αi and fi :
ˆ f
E|ˆ i − αi | = O(n−γ ) and
α E ˆi − fi
f 1 = O(n−β )
where β corresponds to optimal rates for classical function classes.
L. Rouvière (Crest Ensai) 4 / 28

5. Mixture density model
Let Y be a real random variable drawn from a mixture density
model
M
f (x) = αi fi (x).
i=1
The number of components M is known.
The problem
Find efficient estimators αi and ˆi of αi and fi :
ˆ f
E|ˆ i − αi | = O(n−γ ) and
α E ˆi − fi
f 1 = O(n−β )
where β corresponds to optimal rates for classical function classes.
L. Rouvière (Crest Ensai) 4 / 28

6. A classical problem
A number of practical methods have been proposed including
parametric approaches: EM algorithm (Dempster, 1977)
nonparametric techniques (Hall and Zhou, 2003)
Bayesian algorithms (Biernacki, Celeux and Govaert, 2000)
model selection methods (Maugis-Rabusseau and Michel, 2012)
and numerous other ad hoc rules
The classification approach
The mixture components origin are identified by a random variable I
which takes values in {1, . . . , M}. I represent the group or label of Y
L. Rouvière (Crest Ensai) 5 / 28

7. A classical problem
A number of practical methods have been proposed including
parametric approaches: EM algorithm (Dempster, 1977)
nonparametric techniques (Hall and Zhou, 2003)
Bayesian algorithms (Biernacki, Celeux and Govaert, 2000)
model selection methods (Maugis-Rabusseau and Michel, 2012)
and numerous other ad hoc rules
The classification approach
The mixture components origin are identified by a random variable I
which takes values in {1, . . . , M}. I represent the group or label of Y
L. Rouvière (Crest Ensai) 5 / 28

8. A simple solution: labels are observed
Let I be a random variable taking values in {1, . . . , M} which
represents the label or group of Y ;
fi is the density of the conditional distribution L(Y |I = i);
Given n pairs (Y1 , I1 ), . . . , (Yn , In ) drawn frow the distribution of
(Y , I)
it is easy to define efficient estimates of αi and fi :
n
Ni 1Ni >0
αi =
¯ and ¯i,h (t) =
f Kt,h (Yk )1i (Ik ) ,
n Ni
k =1
where
1 t −y
Ni = Card{k = 1, . . . , n : Ik = i} and Kt,h (y ) = K .
h h
But Ik , k = 1, . . . , n are not observed...
L. Rouvière (Crest Ensai) 6 / 28

9. A simple solution: labels are observed
Let I be a random variable taking values in {1, . . . , M} which
represents the label or group of Y ;
fi is the density of the conditional distribution L(Y |I = i);
Given n pairs (Y1 , I1 ), . . . , (Yn , In ) drawn frow the distribution of
(Y , I)
it is easy to define efficient estimates of αi and fi :
n
Ni 1Ni >0
αi =
¯ and ¯i,h (t) =
f Kt,h (Yk )1i (Ik ) ,
n Ni
k =1
where
1 t −y
Ni = Card{k = 1, . . . , n : Ik = i} and Kt,h (y ) = K .
h h
But Ik , k = 1, . . . , n are not observed...
L. Rouvière (Crest Ensai) 6 / 28

10. A simple solution: labels are observed
Let I be a random variable taking values in {1, . . . , M} which
represents the label or group of Y ;
fi is the density of the conditional distribution L(Y |I = i);
Given n pairs (Y1 , I1 ), . . . , (Yn , In ) drawn frow the distribution of
(Y , I)
it is easy to define efficient estimates of αi and fi :
n
Ni 1Ni >0
αi =
¯ and ¯i,h (t) =
f Kt,h (Yk )1i (Ik ) ,
n Ni
k =1
where
1 t −y
Ni = Card{k = 1, . . . , n : Ik = i} and Kt,h (y ) = K .
h h
But Ik , k = 1, . . . , n are not observed...
L. Rouvière (Crest Ensai) 6 / 28

11. Covariates
Assume that one can obtain information on the label I of Y
through an observed covariate X
L. Rouvière (Crest Ensai) 7 / 28

12. Covariates
Assume that one can obtain information on the label I of Y
through an observed covariate X
X2
Y
X1
L. Rouvière (Crest Ensai) 7 / 28

13. Covariates
Assume that one can obtain information on the label I of Y
through an observed covariate X
X2
Y
X1
L. Rouvière (Crest Ensai) 7 / 28

14. Covariates
Assume that one can obtain information on the label I of Y
through an observed covariate X
X2
Y
X1
L. Rouvière (Crest Ensai) 7 / 28

15. Covariates
Assume that one can obtain information on the label I of Y
through an observed covariate X
X2
Y
X1
The (available) data
To estimate both αi and fi we have at hand n random pairs
(Y1 , X1 ), . . . , (Yn , Xn ) extracted from (Y1 , X1 , I1 ), . . . , (Yn , Xn , In ).
L. Rouvière (Crest Ensai) 7 / 28

16. Our strategy
We propose a two stage algorithm:
1 perform a clustering algorithm on X1 , . . . , Xn to guess the labels Ik
of the random pairs (Yk , Xk ).
2 estimate the conditional densities fi using a kernel density
estimate on each cluster:
n
ˆi (t) = ˆi,h (t) = 1
f f Kt,h (Yk )1{i} (ˆk )
I
ˆ
Ni k =1
where ˆk is the predicted label and
I
ˆ i = Card{k = 1, . . . , n : ˆk = i}.
N I
Our mission
1 Evaluate the impact of the performances of the clustering
procedures on the performances of ˆi .
f
2 Propose efficient clustering methods.
L. Rouvière (Crest Ensai) 8 / 28

17. Our strategy
We propose a two stage algorithm:
1 perform a clustering algorithm on X1 , . . . , Xn to guess the labels Ik
of the random pairs (Yk , Xk ).
2 estimate the conditional densities fi using a kernel density
estimate on each cluster:
n
ˆi (t) = ˆi,h (t) = 1
f f Kt,h (Yk )1{i} (ˆk )
I
ˆ
Ni k =1
where ˆk is the predicted label and
I
ˆ i = Card{k = 1, . . . , n : ˆk = i}.
N I
Our mission
1 Evaluate the impact of the performances of the clustering
procedures on the performances of ˆi .
f
2 Propose efficient clustering methods.
L. Rouvière (Crest Ensai) 8 / 28

18. 1 Introduction
2 The model
Notations and examples
Main results
3 Clustering methods
A toy example
Disjoint support densities
L. Rouvière (Crest Ensai) 9 / 28

19. Notations
(Y1 , X1 , I1 ), . . . , (Yn , Xn , In ) n i.i.d. random variables wich take
values in R × Rd × {1, . . . , M}.
Recall that fi is the density of L(Y |I = i) and αi = P(Y = i).
We assume that the conditional distribution L(X |I = i) admits a
density gi,n which could depend on n.
Remark
The dependence between Y and X is not specified in this model
(X = Y is included in the model).
Only the conditional densities gi,n are allowed to depend on n.
L. Rouvière (Crest Ensai) 10 / 28

20. Notations
(Y1 , X1 , I1 ), . . . , (Yn , Xn , In ) n i.i.d. random variables wich take
values in R × Rd × {1, . . . , M}.
Recall that fi is the density of L(Y |I = i) and αi = P(Y = i).
We assume that the conditional distribution L(X |I = i) admits a
density gi,n which could depend on n.
Remark
The dependence between Y and X is not specified in this model
(X = Y is included in the model).
Only the conditional densities gi,n are allowed to depend on n.
L. Rouvière (Crest Ensai) 10 / 28

21. Notations
(Y1 , X1 , I1 ), . . . , (Yn , Xn , In ) n i.i.d. random variables wich take
values in R × Rd × {1, . . . , M}.
Recall that fi is the density of L(Y |I = i) and αi = P(Y = i).
We assume that the conditional distribution L(X |I = i) admits a
density gi,n which could depend on n.
Remark
The dependence between Y and X is not specified in this model
(X = Y is included in the model).
Only the conditional densities gi,n are allowed to depend on n.
L. Rouvière (Crest Ensai) 10 / 28

22. Performance of the clustering method
Assume we are given a clustering procedure which split the
ˆ ˆ ˆ
sample {X1 , . . . , Xn } into M + 1 clusters C0 , C1 , . . . , CM :
M
ˆ
Ci = {X1 , . . . , Xn } and ˆ ˆ
∀i = j, Ci ∩ Cj = ∅.
i=0
ˆ
The cluster C0 (which could be empty) contains unpredicted
observations.
The predicted labels are defined by
ˆ
ˆk = ˆ k ) = j if Xk ∈ Cj
I I(X
0 otherwise.
Performance
The missclassification error of the clustering method is
ϕn = max max P(ˆk = j|Ik = j).
I
1≤k ≤n 1≤i≤M
L. Rouvière (Crest Ensai) 11 / 28

23. Performance of the clustering method
Assume we are given a clustering procedure which split the
ˆ ˆ ˆ
sample {X1 , . . . , Xn } into M + 1 clusters C0 , C1 , . . . , CM :
M
ˆ
Ci = {X1 , . . . , Xn } and ˆ ˆ
∀i = j, Ci ∩ Cj = ∅.
i=0
ˆ
The cluster C0 (which could be empty) contains unpredicted
observations.
The predicted labels are defined by
ˆ
ˆk = ˆ k ) = j if Xk ∈ Cj
I I(X
0 otherwise.
Performance
The missclassification error of the clustering method is
ϕn = max max P(ˆk = j|Ik = j).
I
1≤k ≤n 1≤i≤M
L. Rouvière (Crest Ensai) 11 / 28

24. Performance of the clustering method
Assume we are given a clustering procedure which split the
ˆ ˆ ˆ
sample {X1 , . . . , Xn } into M + 1 clusters C0 , C1 , . . . , CM :
M
ˆ
Ci = {X1 , . . . , Xn } and ˆ ˆ
∀i = j, Ci ∩ Cj = ∅.
i=0
ˆ
The cluster C0 (which could be empty) contains unpredicted
observations.
The predicted labels are defined by
ˆ
ˆk = ˆ k ) = j if Xk ∈ Cj
I I(X
0 otherwise.
Performance
The missclassification error of the clustering method is
ϕn = max max P(ˆk = j|Ik = j).
I
1≤k ≤n 1≤i≤M
L. Rouvière (Crest Ensai) 11 / 28

25. A toy example
Here M = 2 and the conditionnal distributions gi,n are given by
g1,n (x) = g1 (x) = 1[0,1] (x) and g2,n (x) = 1[1−λn ,2−λn ] (x).
L. Rouvière (Crest Ensai) 12 / 28

26. A toy example
Here M = 2 and the conditionnal distributions gi,n are given by
g1,n (x) = g1 (x) = 1[0,1] (x) and g2,n (x) = 1[1−λn ,2−λn ] (x).
Ik = 1 Ik = 1 or 2 Ik = 2
ˆ = 1
Ik ˆ = 0
Ik ˆ = 2
Ik
0 1 2
λn λn
ˆ
λn ˆ
λn
L. Rouvière (Crest Ensai) 12 / 28

27. A toy example
Here M = 2 and the conditionnal distributions gi,n are given by
g1,n (x) = g1 (x) = 1[0,1] (x) and g2,n (x) = 1[1−λn ,2−λn ] (x).
Ik = 1 Ik = 1 or 2 Ik = 2
ˆ = 1
Ik ˆ = 0
Ik ˆ = 2
Ik
0 1 2
λn λn
ˆ
λn ˆ
λn
L. Rouvière (Crest Ensai) 12 / 28

28. A more realistic situation
We assume that the supports Si,n of gi,n are disjoint connected
compact sets. Let
δn = min d(Si,n , Sj,n ).
i=j
δn
L. Rouvière (Crest Ensai) 13 / 28

29. Recall that
n
ˆi (t) = ˆi,h (t) = 1
f f Kt,h (Yk )1{i} (ˆk )
I
ˆ
Ni k =1
and
n
¯i (t) = ¯i,h (t) = 1Ni >0
f f Kt,h (Yk )1{i} (Ik ).
Ni
k =1
ˆ
Moreover, we set αi = Ni /n.
ˆ
Theorem
For all n ≥ 1 and i = 1, . . . , M, there exists A1 > 0, A2 > 0 and A3 > 0
such that
E ˆi − fi
f 1 ≤ E ¯i − fi
f 1 + A1 ϕn + A2 exp(−n)
and
E|ˆ i − αi | ≤ A3 ϕn .
α
Remark
The bound is nonasymptotic.
L. Rouvière (Crest Ensai) 14 / 28

30. Theorem
For all n ≥ 1 and i = 1, . . . , M, there exists A1 > 0, A2 > 0 and A3 > 0
such that
E ˆi − fi
f 1 ≤ E ¯i − fi
f 1 + A1 ϕn + A2 exp(−n)
and
E|ˆ i − αi | ≤ A3 ϕn .
α
Remark
The bound is nonasymptotic.
If ϕn tends to zero much faster than E ¯i − fi 1 than the
f
performance of ˆi is guaranted to be equivalent to the performance
f
of the ideal estimate ¯i .
f
L. Rouvière (Crest Ensai) 14 / 28

31. Theorem
For all n ≥ 1 and i = 1, . . . , M, there exists A1 > 0, A2 > 0 and A3 > 0
such that
E ˆi − fi
f 1 ≤ E ¯i − fi
f 1 + A1 ϕn + A2 exp(−n)
and
E|ˆ i − αi | ≤ A3 ϕn .
α
Remark
The bound is nonasymptotic.
If ϕn tends to zero much faster than E ¯i − fi 1 than the
f
performance of ˆi is guaranted to be equivalent to the performance
f
of the ideal estimate ¯i .
f
L. Rouvière (Crest Ensai) 14 / 28

32. Lipschitz class
Definition
Let s ∈ N and C > 0. We call W(s, C) the Lipschitz with parameters
s, C the class of all densities on [0, 1] with s − 1 asolutely continous
derivatives for which for all x, y ∈ R,
|f (s) (x) − f (s) (y )| ≤ C|x − y |.
Optimal rate
The minimax L1 risk for compactly supported Lipschitz class W(s, L) is
of order n−s/(2s+1) (see Devroye and Györfi, 1985).
L. Rouvière (Crest Ensai) 15 / 28

33. Lipschitz class
Definition
Let s ∈ N and C > 0. We call W(s, C) the Lipschitz with parameters
s, C the class of all densities on [0, 1] with s − 1 asolutely continous
derivatives for which for all x, y ∈ R,
|f (s) (x) − f (s) (y )| ≤ C|x − y |.
Optimal rate
The minimax L1 risk for compactly supported Lipschitz class W(s, L) is
of order n−s/(2s+1) (see Devroye and Györfi, 1985).
L. Rouvière (Crest Ensai) 15 / 28

34. An example of rate of convergence
Corollary
Assume that fi belongs to W(s, L). Moreover if ϕn = o(n−s/(2s+1) ), then
E ˆi − fi
f 1 = O n−s/(2s+1) .
(under classical assumptions on K and hi,n ).
An important complement
Provide clustering procedures such that ϕn = o(n−s/(2s+1) ).
L. Rouvière (Crest Ensai) 16 / 28

35. An example of rate of convergence
Corollary
Assume that fi belongs to W(s, L). Moreover if ϕn = o(n−s/(2s+1) ), then
E ˆi − fi
f 1 = O n−s/(2s+1) .
(under classical assumptions on K and hi,n ).
An important complement
Provide clustering procedures such that ϕn = o(n−s/(2s+1) ).
L. Rouvière (Crest Ensai) 16 / 28

36. 1 Introduction
2 The model
Notations and examples
Main results
3 Clustering methods
A toy example
Disjoint support densities
L. Rouvière (Crest Ensai) 17 / 28

37. Here M = 2 and the conditionnal distributions gi,n are given by
g1,n (x) = g1 (x) = 1[0,1] (x) and g2,n (x) = 1[1−λn ,2−λn ] (x).
L. Rouvière (Crest Ensai) 18 / 28

38. Here M = 2 and the conditionnal distributions gi,n are given by
g1,n (x) = g1 (x) = 1[0,1] (x) and g2,n (x) = 1[1−λn ,2−λn ] (x).
Ik = 1 Ik = 1 or 2 Ik = 2
ˆ = 1
Ik ˆ = 0
Ik ˆ = 2
Ik
0 1 2
λn λn
ˆ
λn ˆ
λn
L. Rouvière (Crest Ensai) 18 / 28

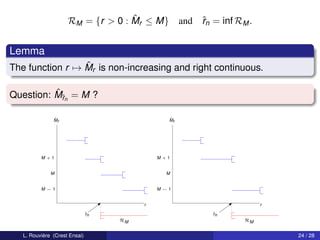
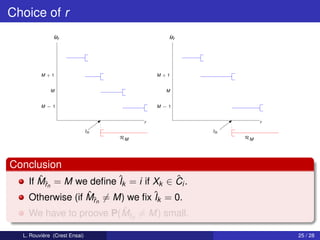
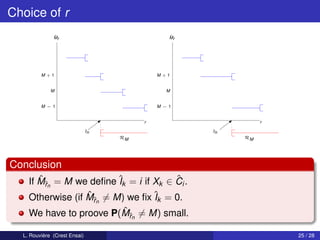
39. Here M = 2 and the conditionnal distributions gi,n are given by
g1,n (x) = g1 (x) = 1[0,1] (x) and g2,n (x) = 1[1−λn ,2−λn ] (x).
Ik = 1 Ik = 1 or 2 Ik = 2
ˆ = 1
Ik ˆ = 0
Ik ˆ = 2
Ik
0 1 2
λn λn
ˆ
λn ˆ
λn
ˆ
We choose λn = 2 − X(n) and

ˆ
1 if Xk ≤ 1 − λn

ˆk = 0 if 1 − λn < Xk < 1
I ˆ

2 if Xk ≥ 1.

L. Rouvière (Crest Ensai) 18 / 28

40. Here M = 2 and the conditionnal distributions gi,n are given by
g1,n (x) = g1 (x) = 1[0,1] (x) and g2,n (x) = 1[1−λn ,2−λn ] (x).
Ik = 1 Ik = 1 or 2 Ik = 2
ˆ = 1
Ik ˆ = 0
Ik ˆ = 2
Ik
0 1 2
λn λn
ˆ
λn ˆ
λn
ˆ
We choose λn = 2 − X(n) and

ˆ
1 if Xk ≤ 1 − λn

ˆk = 0 if 1 − λn < Xk < 1
I ˆ

2 if Xk ≥ 1.

Find an upper boud of
ϕn = max max P(ˆk = j|Ik = j).
I
1≤k ≤n 1≤i≤M
L. Rouvière (Crest Ensai) 18 / 28

41. Result
Proposition
The performance ϕn of the proposed clustering procedure satisfy:
log n
ϕn = λn + O .
n
Remark
√
In particular, if λn = o(n−α ) for α ≥ 1/2 then ϕn = o(1/ n) and for n
large enough
E ˆi − fi 1 ≈ E ¯i − fi 1
f f
for fi in W(s, L).
L. Rouvière (Crest Ensai) 19 / 28

42. Result
Proposition
The performance ϕn of the proposed clustering procedure satisfy:
log n
ϕn = λn + O .
n
Remark
√
In particular, if λn = o(n−α ) for α ≥ 1/2 then ϕn = o(1/ n) and for n
large enough
E ˆi − fi 1 ≈ E ¯i − fi 1
f f
for fi in W(s, L).
L. Rouvière (Crest Ensai) 19 / 28

43. We assume that the supports Si,n of gi,n are disjoint connected
compact sets. Let δn = mini=j d(Si,n , Sj,n ).
δn
The idea is to select a radius ˆn such that:
r
Si,n ≈ B(Xk , ˆn ).
r
k ∈Ji
L. Rouvière (Crest Ensai) 20 / 28

44. We assume that the supports Si,n of gi,n are disjoint connected
compact sets. Let δn = mini=j d(Si,n , Sj,n ).
δn
The idea is to select a radius ˆn such that:
r
Si,n ≈ B(Xk , ˆn ).
r
k ∈Ji
L. Rouvière (Crest Ensai) 20 / 28

45. Covering supports
2.0
1.5
1.0
X2
0.5
0.0
0.0 0.5 1.0 1.5 2.0 2.5 3.0
X1
L. Rouvière (Crest Ensai) 21 / 28

46. Covering supports
2.0
1.5
1.0
X2
0.5
0.0
0.0 0.5 1.0 1.5 2.0 2.5 3.0
X1
L. Rouvière (Crest Ensai) 21 / 28

47. Covering supports
2.0
1.5
1.0
X2
0.5
0.0
0.0 0.5 1.0 1.5 2.0 2.5 3.0
X1
L. Rouvière (Crest Ensai) 21 / 28

48. Covering supports
2.0
1.5
1.0
X2
0.5
0.0
0.0 0.5 1.0 1.5 2.0 2.5 3.0
X1
L. Rouvière (Crest Ensai) 21 / 28

49. Covering supports
2.0
1.5
1.0
X2
0.5
0.0
0.0 0.5 1.0 1.5 2.0 2.5 3.0
X1
L. Rouvière (Crest Ensai) 21 / 28

50. Covering supports
2.0
1.5
1.0
X2
0.5
0.0
0.0 0.5 1.0 1.5 2.0 2.5 3.0
X1
L. Rouvière (Crest Ensai) 21 / 28

51. The algorithm
For r > 0 let A = (Ak ,k )1≤k ,k ≤n defined by
1 if Xk − Xk 2 ≤ 2r ⇐⇒ B(Xk , r ) ∩ B(Xk , r ) = ∅
Ak ,k =
0 otherwise.
This matrix induces a non-oriented graph and two different
observations Xk and Xk belong to the same cluster if k and k
belong to the same connected component of the graph.
ˆ
Let Mr be the number of clusters (connected components) and
ˆ ˆˆ
denote by C1 , . . . , CMr the associated clusters.
L. Rouvière (Crest Ensai) 22 / 28

52. The algorithm
For r > 0 let A = (Ak ,k )1≤k ,k ≤n defined by
1 if Xk − Xk 2 ≤ 2r ⇐⇒ B(Xk , r ) ∩ B(Xk , r ) = ∅
Ak ,k =
0 otherwise.
This matrix induces a non-oriented graph and two different
observations Xk and Xk belong to the same cluster if k and k
belong to the same connected component of the graph.
ˆ
Let Mr be the number of clusters (connected components) and
ˆ ˆˆ
denote by C1 , . . . , CMr the associated clusters.
L. Rouvière (Crest Ensai) 22 / 28

53. The algorithm
For r > 0 let A = (Ak ,k )1≤k ,k ≤n defined by
1 if Xk − Xk 2 ≤ 2r ⇐⇒ B(Xk , r ) ∩ B(Xk , r ) = ∅
Ak ,k =
0 otherwise.
This matrix induces a non-oriented graph and two different
observations Xk and Xk belong to the same cluster if k and k
belong to the same connected component of the graph.
ˆ
Let Mr be the number of clusters (connected components) and
ˆ ˆˆ
denote by C1 , . . . , CMr the associated clusters.
L. Rouvière (Crest Ensai) 22 / 28

54. Example
r large r small
 
1 1 0 0 0 ...
 
1 1 0 1 1 ...
1 1 1 1 1 . . .  1 1 0 0 0 . . .
A = 0 0 1 0 0 . . .
 
A = 0 1 1 1 1 . . . 
 
 
. . . . . .
 
. . . . . .
. . . . . . . . . . . .
. . . . . . . . . . . .
ˆ
Mr small. ˆ
Mr large.
Practical construction
Depth-First seach algorithm (Cormen, Leiserson and Rivest (2001))
allows to extract the connected components of A
L. Rouvière (Crest Ensai) 23 / 28

55. Example
r large r small
 
1 1 0 0 0 ...
 
1 1 0 1 1 ...
1 1 1 1 1 . . .  1 1 0 0 0 . . .
A = 0 0 1 0 0 . . .
 
A = 0 1 1 1 1 . . . 
 
 
. . . . . .
 
. . . . . .
. . . . . . . . . . . .
. . . . . . . . . . . .
ˆ
Mr small. ˆ
Mr large.
Practical construction
Depth-First seach algorithm (Cormen, Leiserson and Rivest (2001))
allows to extract the connected components of A
L. Rouvière (Crest Ensai) 23 / 28

56. ˆ
RM = {r > 0 : Mr ≤ M} and ˆn = inf RM .
r
Lemma
ˆ
The function r → Mr is non-increasing and right continuous.
ˆr
Question: Mˆn = M ?
L. Rouvière (Crest Ensai) 24 / 28

57. ˆ
RM = {r > 0 : Mr ≤ M} and ˆn = inf RM .
r
Lemma
ˆ
The function r → Mr is non-increasing and right continuous.
ˆr
Question: Mˆn = M ?
L. Rouvière (Crest Ensai) 24 / 28

58. ˆ
RM = {r > 0 : Mr ≤ M} and ˆn = inf RM .
r
Lemma
ˆ
The function r → Mr is non-increasing and right continuous.
ˆr
Question: Mˆn = M ?
L. Rouvière (Crest Ensai) 24 / 28

59. ˆ
RM = {r > 0 : Mr ≤ M} and ˆn = inf RM .
r
Lemma
ˆ
The function r → Mr is non-increasing and right continuous.
ˆr
Question: Mˆn = M ?
ˆ
Mr ˆ
Mr
M +1 M +1
M M
M −1 M −1
r r
ˆn
r ˆn
r
RM RM
L. Rouvière (Crest Ensai) 24 / 28

60. Choice of r
ˆ
Mr ˆ
Mr
M +1 M +1
M M
M −1 M −1
r r
ˆn
r ˆn
r
RM RM
Conclusion
ˆr I ˆ
If Mˆn = M we define ˆk = i if Xk ∈ Ci .
Otherwise (if Mˆ = M) we fix ˆk = 0.
ˆr In
ˆr
We have to proove P(Mˆn = M) small.
L. Rouvière (Crest Ensai) 25 / 28

61. Choice of r
ˆ
Mr ˆ
Mr
M +1 M +1
M M
M −1 M −1
r r
ˆn
r ˆn
r
RM RM
Conclusion
ˆr I ˆ
If Mˆn = M we define ˆk = i if Xk ∈ Ci .
Otherwise (if Mˆ = M) we fix ˆk = 0.
ˆr In
ˆr
We have to proove P(Mˆn = M) small.
L. Rouvière (Crest Ensai) 25 / 28

62. Technical assumptions
H1 The density gn = i αi gi,n is uniformely minorated on its support.
More precisely:
tn = inf gn (x) > 0 where Sn = Si,n . (1)
x∈Sn
i
L. Rouvière (Crest Ensai) 26 / 28

63. Technical assumptions
H2 There exists N ∈ N , a family of euclidan balls {B } =1,...,N with
radius rn /2 and two positive constants c1 and c2 such that:
Sn ⊂ N B

 =1
Leb(Sn ) ≥ c1 N Leb(Sn ∩ B )
=1

 d
∀ = 1, . . . , N, Leb(Sn ∩ B ) ≥ c2 rn
where
d (log n)2
rn = .
ntn
L. Rouvière (Crest Ensai) 26 / 28

64. Technical assumptions
H2 There exists N ∈ N , a family of euclidan balls {B } =1,...,N with
radius rn /2 and two positive constants c1 and c2 such that:
Sn ⊂ N B

 =1
Leb(Sn ) ≥ c1 N Leb(Sn ∩ B )
=1

 d
∀ = 1, . . . , N, Leb(Sn ∩ B ) ≥ c2 rn
where
d (log n)2
rn = .
ntn
H2 is satisfied when the supports Si,n are smoothes and don’t
depend on n (see Biau, Cadre, Pelletier (2008)).
c2 allows (to some extent) to measure the regularity of the
supports (c2 is large for regular supports).
L. Rouvière (Crest Ensai) 26 / 28

65. Result
Theorem
Assume that H1 and H2 are satisfied. Moreover assume that
1/d
(log n)2
δn > 2 ,
ntn
then for a > 0 such that log n ≥ (1 + a)/c2 , we have for A4 > 0
ˆr ˆ
P {Mˆn = M} ∩ {∀i Ci ⊂ Si,n } ≥ 1 − A4 n−a .
Corollary
1 ˆr
Mˆn = M almost surely for n large enough.
2 The misclassification error ϕn is bounded by
ϕn = max max P(ˆk = i|Ik = i) = O(n−a ).
I
i=1,...,M k =1,...,n
L. Rouvière (Crest Ensai) 27 / 28

66. Result
Theorem
Assume that H1 and H2 are satisfied. Moreover assume that
1/d
(log n)2
δn > 2 ,
ntn
then for a > 0 such that log n ≥ (1 + a)/c2 , we have for A4 > 0
ˆr ˆ
P {Mˆn = M} ∩ {∀i Ci ⊂ Si,n } ≥ 1 − A4 n−a .
Corollary
1 ˆr
Mˆn = M almost surely for n large enough.
2 The misclassification error ϕn is bounded by
ϕn = max max P(ˆk = i|Ik = i) = O(n−a ).
I
i=1,...,M k =1,...,n
L. Rouvière (Crest Ensai) 27 / 28

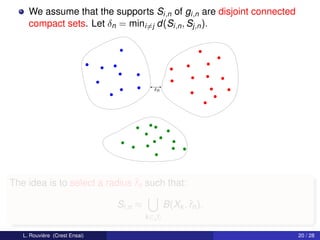
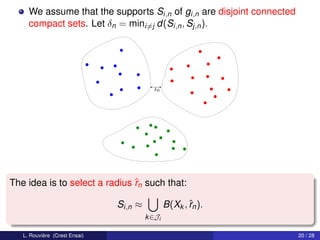
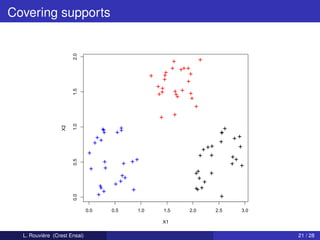
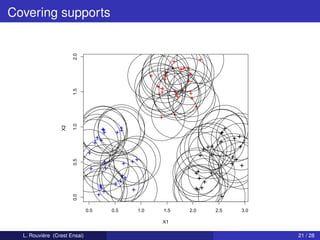
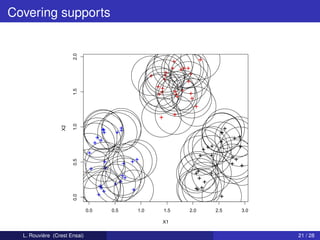
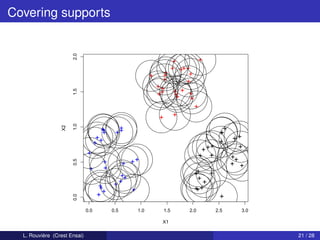
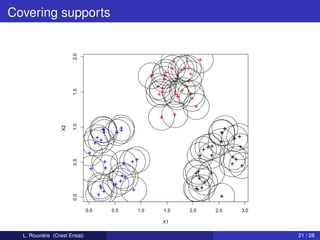
67. Example
Corollary
Assume that gi,n are univariate densities and
tn = n−γ , γ ∈]0, 1[.
Then the kernel density estimate ˆi achieves the optimal rate over the
f
class W(s, L) provided
1/d
(log n)2
δn > 2 .
n1−γ
L. Rouvière (Crest Ensai) 28 / 28

68. H2
H2 implies that the covering number M should verify
n
N ≤ (c1 c2 )−1 .
(log n)2
H2 is clearly satisfied for d = 1.
However for higher dimensions, even if Sn is assumed to be
compact, its diameter can be as large as we want
hn (x, y ) = 1[1−a−1 ,an ] (x)1[0,1/x 2 ] (y ).
n
L. Rouvière (Crest Ensai) 29 / 28