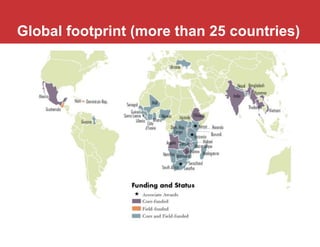
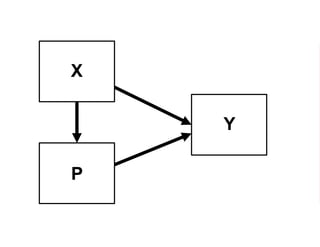
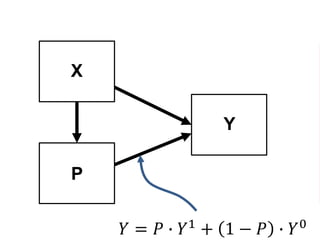
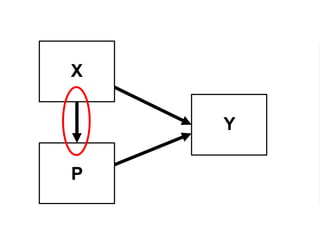
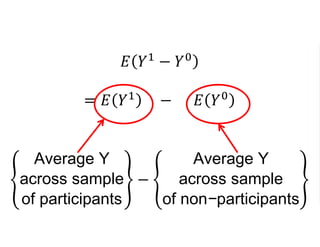
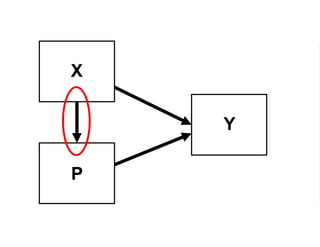
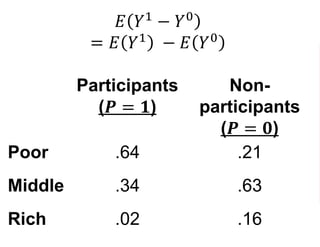
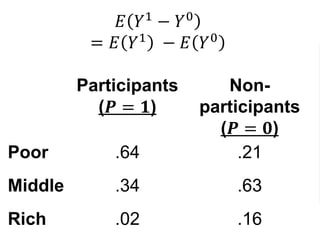
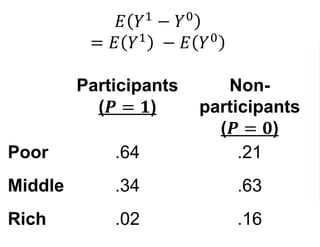
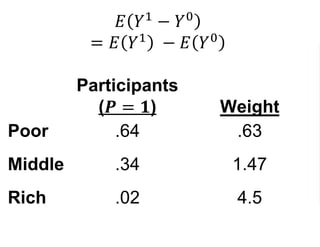
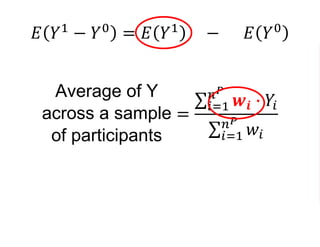
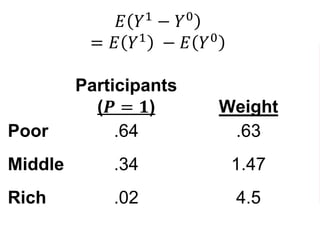
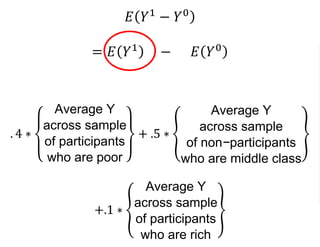
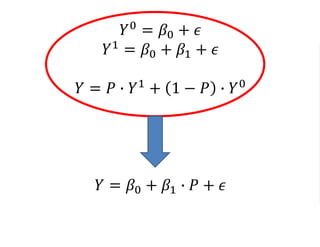
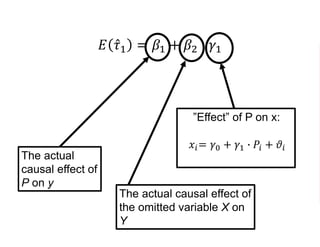
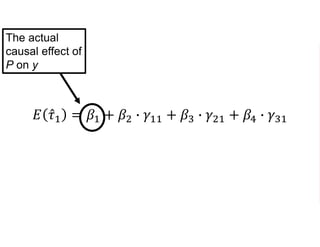
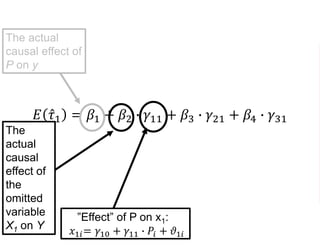
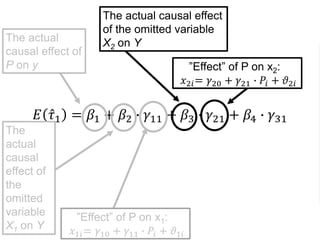
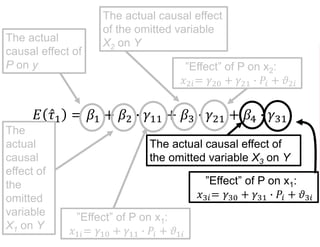
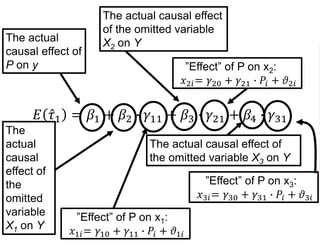
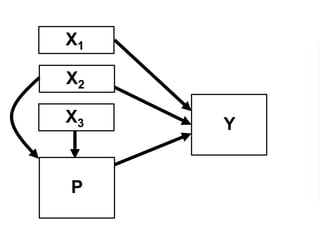
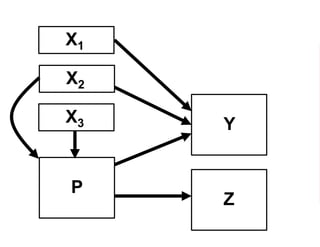
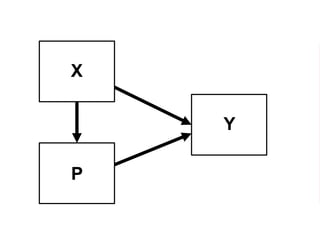
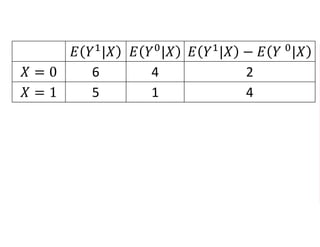
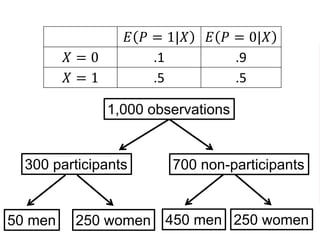
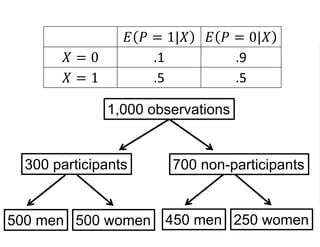
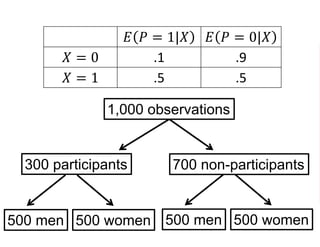
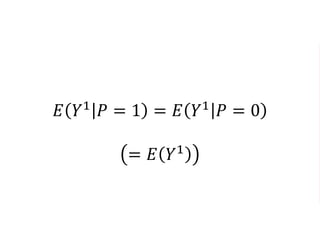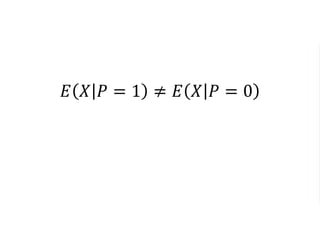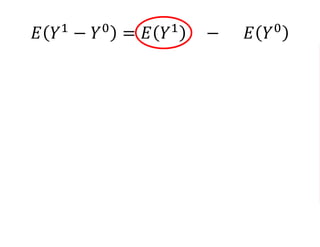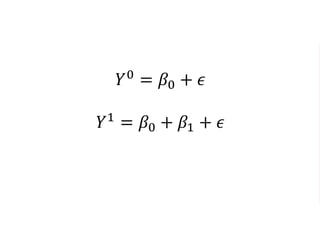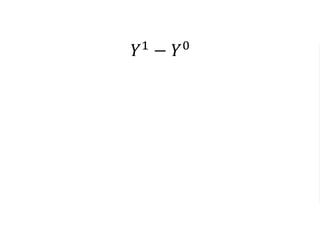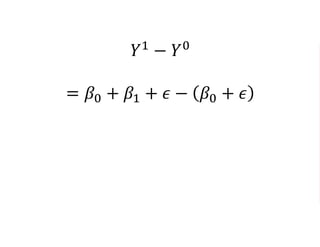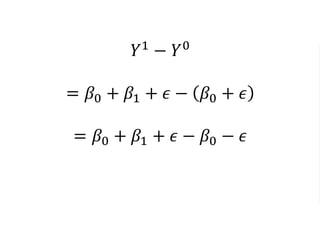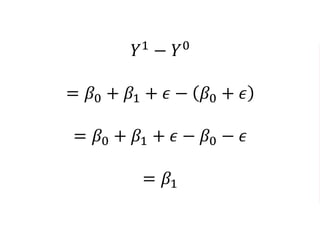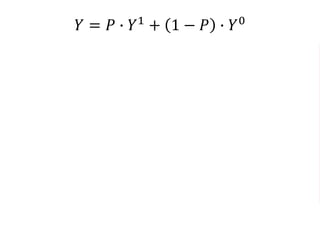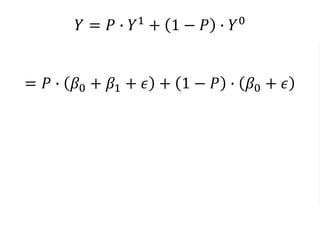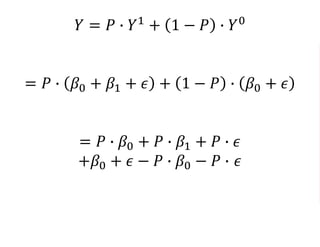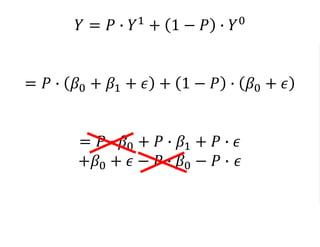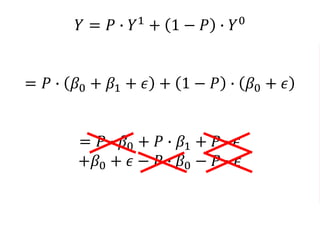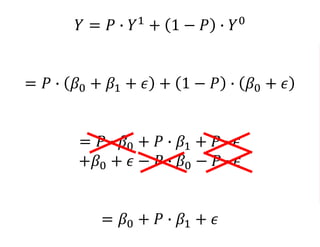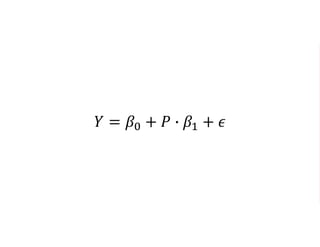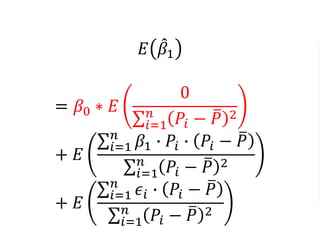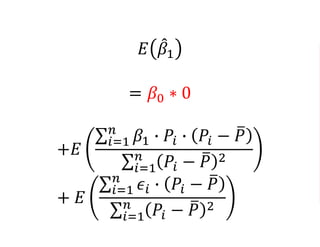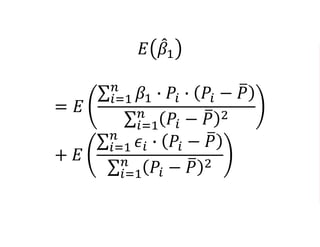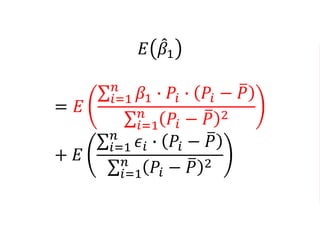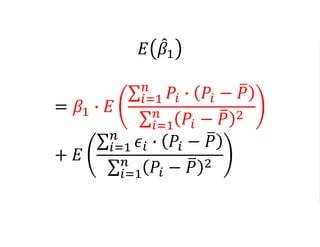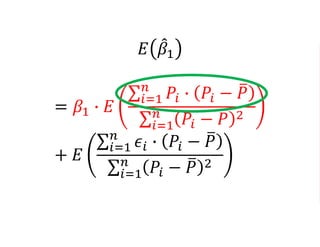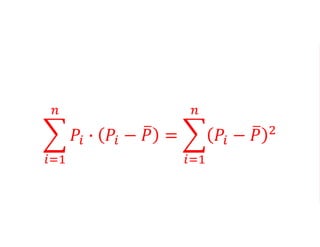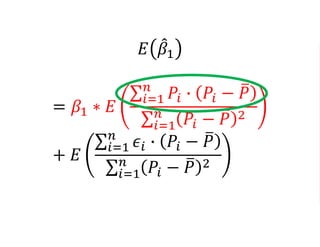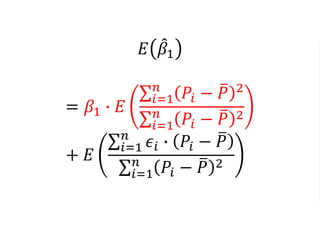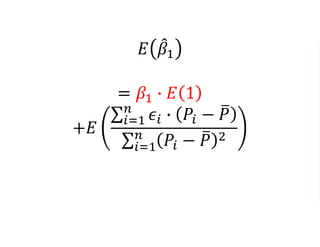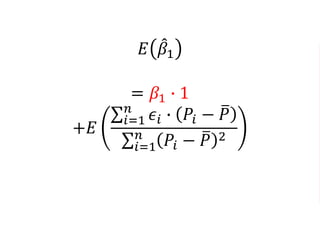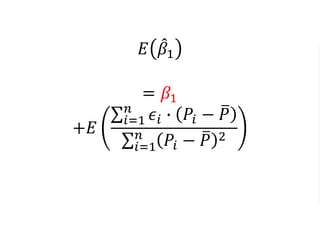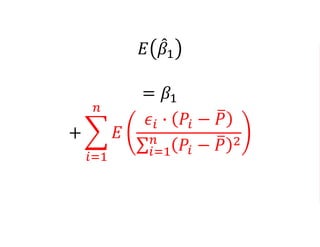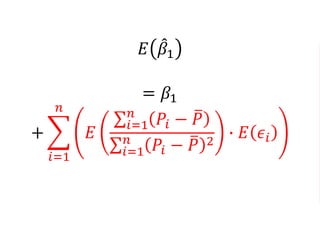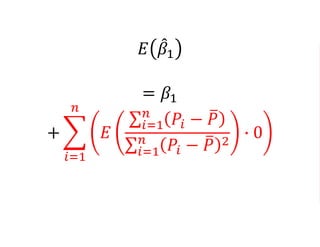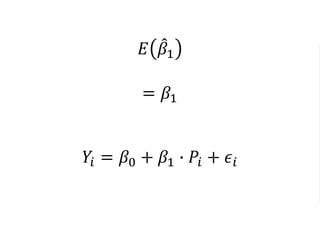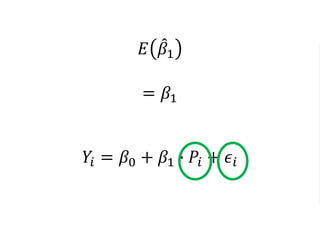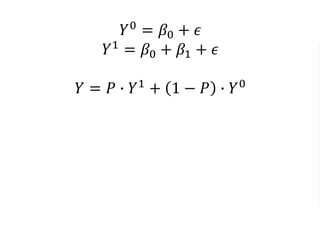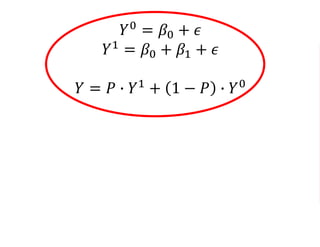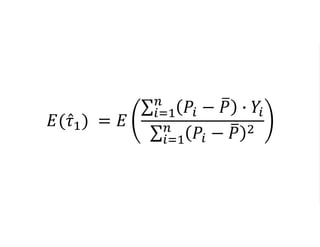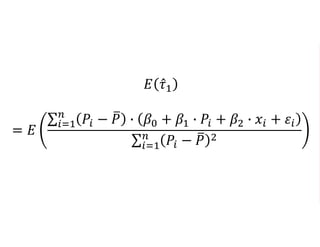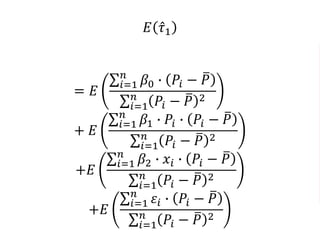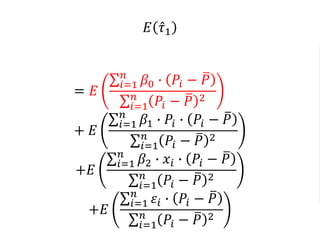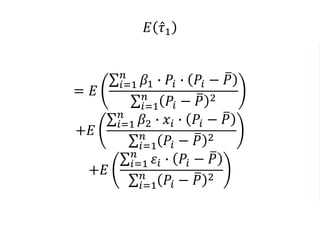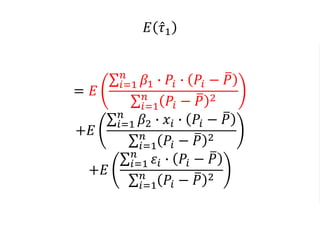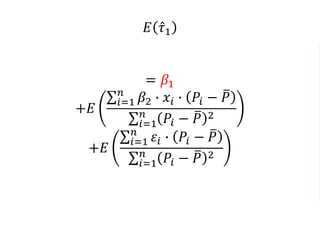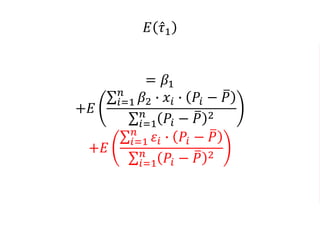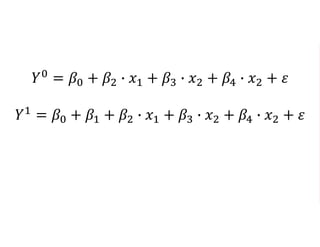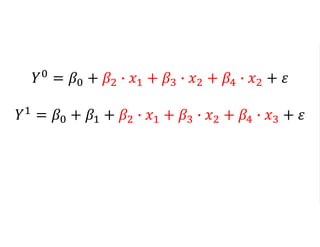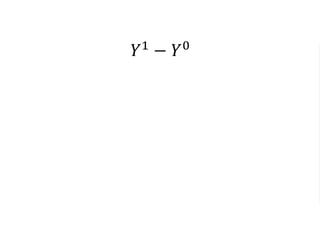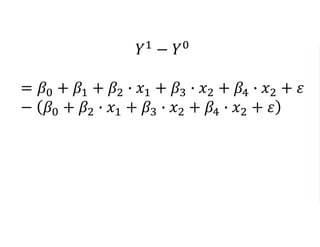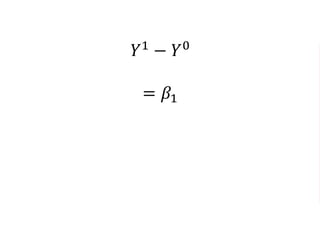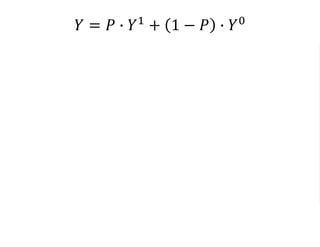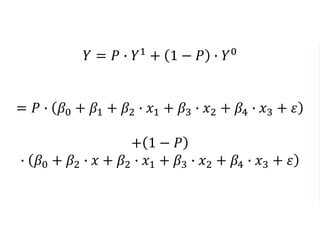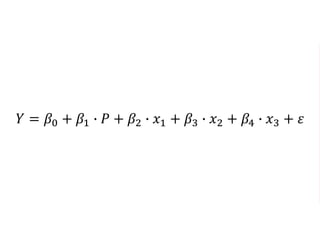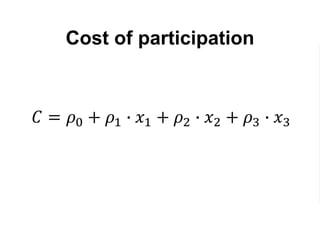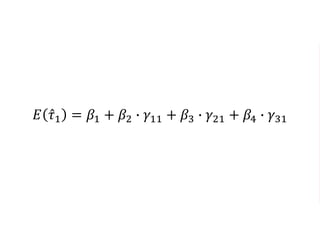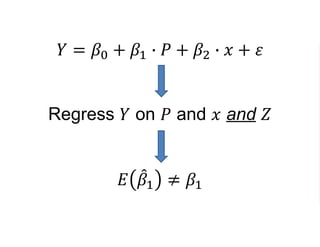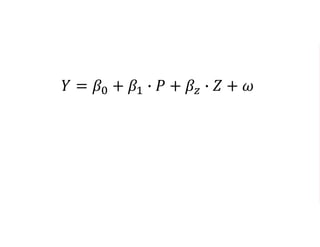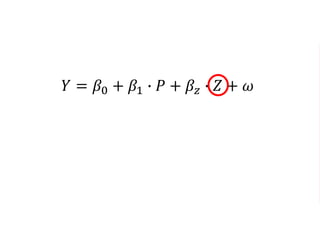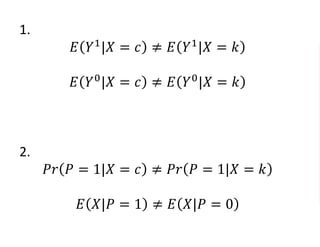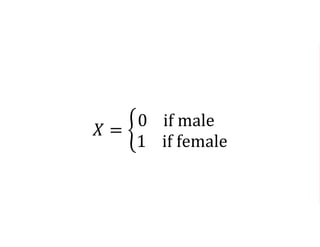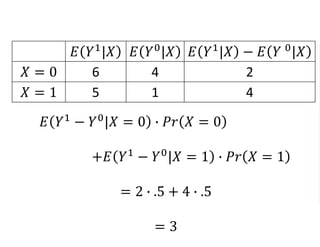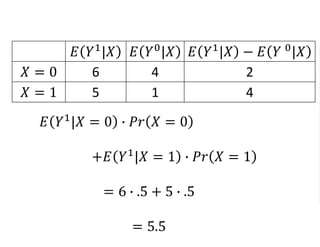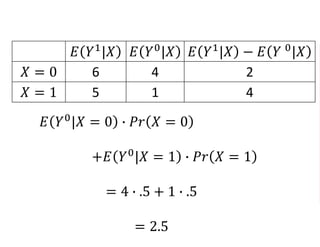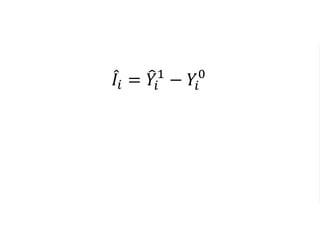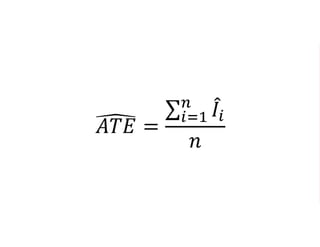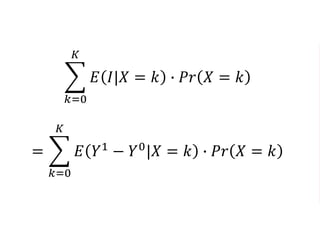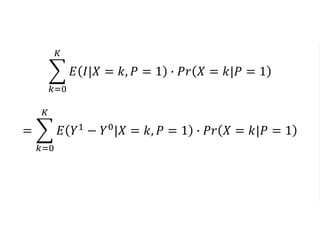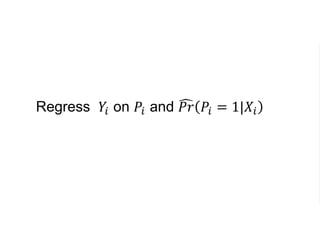The document outlines a five-year cooperative agreement aimed at enhancing health information systems across over 25 countries with a total budget of $180 million. Key objectives include improving data management capabilities, rigorous evaluation methodologies, and better decision-making to support sustained health outcomes. It discusses various statistical approaches and frameworks for evaluating program impacts, emphasizing the importance of effective data collection and analysis.