Tài liệu trình bày về định thức của ma trận vuông trong đại số tuyến tính, bao gồm cách tính định thức cấp 2 và 3 cùng với các ví dụ cụ thể. Nó cũng thảo luận về các tính chất của định thức, các bài tập tính định thức và những quy tắc biến đổi giúp tính toán định thức hiệu quả hơn. Ngoài ra, tài liệu cuối cùng chứng minh một quy luật liên quan đến định thức của tích hai ma trận.

1. 1
BÀI 2
b
= a
d - c
a
c d
b

2. Đại Số Tuyến Tính å §2: Định Thức
1. Với mỗi ma trận vuông A cấp n
a a ...
a
a a ...
a
é ê 11 12 1
n
ù
ú
= ê 21 22 2
n
ú ê ... ... ... ...
ú
ê ú
êë a a a
n 1 n 2
nn
úû
A
...
tồn tại một số thực được gọi là định thức của
ma trận A, được ký hiệu
a a a
a a a
11 12 1
21 22 2
a a a
1 2
...
...
det(A); |A|;
... ... ... ...
...
n
n
n n nn

3. Đại Số Tuyến Tính å
3
§2: Định Thức
 Định thức cấp 2:
11 12
11 22 12 21
21 22
= - .
a a
a a a a
a a
 Ví dụ:
2 3
2.6 5.3 3.
5 6
= - = -

4. Đại Số Tuyến Tính å
4
§2: Định Thức
 Định thức cấp 3:
a a a
a a a
a a a
11 12 13
21 22 23
31 32 33
a a a a a a a a a
a a a a a a a a a
= + +
- + +
( )
11 22 33 31 12 23 13 32 21
( )
13 22 31 33 21 12 11 32 23

5. Đại Số Tuyến Tính å
5
§2: Định Thức
 Ví dụ: Tính
1 2 3
2 4 1
3 5 6
= (1.4.6+3.2.1+3.2.5)
-(3.4.3 +6.2.2 +1.1.5)
=(24+6+30)-(36+24+5)=60-65=-5

6. Đại Số Tuyến Tính å
6
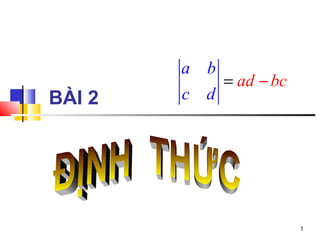
§2: Định Thức
 Bài tập: Tính
3 1 4
5 -
2 0
6 -
1 7
=[ 3.(-2).7+6.1.0+4.5.(-1) ]
-[ 4.(-2).6+7.1.5+3.0.(-1) ]
= -62+13= - 49

7. Đại Số Tuyến Tính å
7
§2: Định Thức
 Ví dụ: Tính
2
1
5
1
4
0
2
-
-
2 1 5
1 4 0
3 6 2
-
-
3
6
= -108
=[2.4.(-2)+1.0.3+5.(-1).6]
-[5.4.3 +2.0.6+1.(-1).(-2)]
=[-16+0-30]-[60+0+2]=-108

8. Đại Số Tuyến Tính å
8
§2: Định Thức
 Bài tập: Tính
2 4 -
1
3 5 6
0 2 3
-
3 1 2
3 4 0
1 2 5
-
-
=
-
-36 +12 = -24
= -55

9. Đại Số Tuyến Tính å
9
§2: Định Thức

10. Đại Số Tuyến Tính å
10
§2: Định Thức
 Ví dụ: Cho ma trận
1 4 3
ù
ú ú ú
û
é
ê ê ê
ë
5 2 1
-
-
=
2 2 1
( 1)
3 6 0
A
A = (-1) 1 + 1
det(M ) =
11 11 6 -
= -6
A = (-1) 1 + 2
det( M ) = 5 1
3 12 12
( 1)
3 0
-
-
= -3
5 2
A = (-1) 1 + 3
det(M ) = ( 1)
4 13 13 3 6
-
-
= 36

11. Đại Số Tuyến Tính å
11
§2: Định Thức
 Bài tập: Với
1 4 3
ù
ú ú ú
û
é
ê ê ê
ë
5 2 1
-
-
=
3 6 0
A
 Tính
A
21
A
23
A
33
=
=
=

12. Đại Số Tuyến Tính å
12
§2: Định Thức

13. Đại Số Tuyến Tính å
13
§2: Định Thức

14. Đại Số Tuyến Tính å
14
§2: Định Thức
 Ví dụ: Tính định thức sau:
-
1 4 3
5 2 1
3 6 0
-
i
a A a A a A
11 12
1
11 12 13 13
==
+ +
= - + - + -
)
= -
1.( 6) 4.( 3) ( 3 .36
126
-
1 4 3
5 2 1
3 6 0
-
j
a A a A a A
13 23
3
13 23 33 33
==
+ +

15. Đại Số Tuyến Tính å
15
§2: Định Thức
 Ví dụ: Tính định thức sau:
2 2 1 0
3 1 2 1
0 4 3 0
5 0 4 2
-
-
-
j
4
a A a A a A a A
14 14 24 24 34 34 44 44
==
+ + +
2 2 1 2 2 1
6 8
= A + - - + A + -
- -
0. 1( 1) 0 4 3 0. ( 2)( 1) 3 1 2
14 34
-
5 0 4 0 4 3
= -18-2(-52) = 86

16. Đại Số Tuyến Tính å
16
§2: Định Thức
 Ví dụ: Tính định thức sau:
-
1 2 3 0
4 -
1 5 1
0 2 -
2 3
1 0 6 0
-
4
2 3 0 1 2 0
5 7
( 1) 1 5 1 ( 1) 4 1 1
2
( 1)
2 3
6
0 2 3
i=
-
-
= - - + - -
-
= (24 -5) - 6(-3- 26)
=19 +174 =193

17. Đại Số Tuyến Tính å
17
§2: Định Thức
 Bài tập: Tính định thức sau
-
1 2 3 1
0 2 4 -
2
1 3 0 -
4
2 0 -
1 5
= 102

18. Đại Số Tuyến Tính å
18
§2: Định Thức
 Tính chất của định thức

19. Đại Số Tuyến Tính å
19
§2: Định Thức
 Ví dụ:
1 2 1 3
= - = -
2. 2
3 4 2 4

20. Đại Số Tuyến Tính å
20
§2: Định Thức

21. Đại Số Tuyến Tính å
21
§2: Định Thức
1 2 3 4
= - =
2; 2.
3 4 1 2
 VD:

22. Đại Số Tuyến Tính å
22
§2: Định Thức

23. Đại Số Tuyến Tính å
23
§2: Định Thức

24. Đại Số Tuyến Tính å
24
§2: Định Thức
 VD:
+ = - + -
2 4 .1 2
.2 1 2
= - = = -
2; 2.
3 5 3 5
2
5
2
3
2 3
2c 2d 3a 3b
a b c d
= + - -
+ +
2 3 2 3
2c 3a 2d 3b
a c b d

25. Đại Số Tuyến Tính å
25
§2: Định Thức

26. Đại Số Tuyến Tính å
26
§2: Định Thức
 Ví dụ:
2 5
3 4 6 8
4 10
A é ù
; 2
A ê
é ù
= ú
= ê ú
ë û ë û
4 10 2.2 2.5 2 5
= = =
det(2 ) 2
6 8 6 8 2.3 2.4
2
2 5
3 4
2.2 2 det( ).
A
A
= =

27. Đại Số Tuyến Tính å
27
§2: Định Thức
(5) Nếu nhân mỗi phần tử của hàng thứ i
với cùng một số rồi cộng vào hàng k thì
định thức không đổi

28. Đại Số Tuyến Tính å
28
§2: Định Thức
 VD:
1 2 3 1 2 3
5 7 9 5 7 9
1 2 3 1 2 3
é ù é ù
= ê ú¾¾¾® = ê ú = ê ú ê ú
êë úû êë úû
det( ) det( ) det( )
det( ) det( )
det( ) 0.
A h 1 «h 3
B A
A = B = -
A
A A
A
Þ = -
Þ =

29. Đại Số Tuyến Tính å
29
§2: Định Thức

30. Đại Số Tuyến Tính å
30
§2: Định Thức
 Ví dụ:
2 0 0 0
0 -
3 0 0
0 0 5 0
0 0 0 1
1
1
1 11 2
3 0 0
0 5 0
0 0 1
i
=
a A
-
= =
1 5 0
i=
= - = -
2.( 3).5.1
0
.
1
2 ( 3)

31. Đại Số Tuyến Tính å
31
§2: Định Thức

32. Đại Số Tuyến Tính å
32
§2: Định Thức
 Ví dụ:
-
1 5 8 2
0 3 6 0
0 0 2 9
0 0 0 5
=1.3.2.5 = 30

33. Đại Số Tuyến Tính å
33
§2: Định Thức
Dùng các tính chất của định thức để
tính định thức:
Phương pháp: Dùng các phép biến đổi có
dạng sau
h h c c
= l = l l
¹
( ), 0
A ¾¾¾¾¾¾® i i i i
B Þ B =
l
A
A ¾¾¾¾¾® h i « h j ( c i «
c
j
)
B Þ B = -
A
A ¾¾¾¾¾¾¾® h = h + l h ( c = c +
l
c
)
B Þ B =
A
det( ) det( ),
det( ) det( ),
det( ) det( ),
i i j i i j
ta đưa định thức đã cho về dạng tam giác.

34. Đại Số Tuyến Tính å
34
§2: Định Thức
 Ví dụ: Tính định thức
1 2 1 3
2 3 1 5
1 6 5 2
3 4 2 7
D
-
=
- -
-
h h h
2 = 2 -2 1
=
-
1 2 1 3
0 - 1 3 -
1
1 6 5 2
3 4 2 7
- -
-
h h h
3= 3+ 1
=
4 4 1 h =h -3h
-
1 2 1 3
0 - 1 3 -
1
0 8 4 1
0 - 2 1 -
2
h h h
3= 3+8 2
=
4 4 2 h =h -2h
-
1 2 1 3
0 - 1 3 -
1
0 0 28 7
0 0 5 0
=
-
-

35. Đại Số Tuyến Tính å
35
§2: Định Thức
c c
3 4 «=
-
1 2 3 1
0 1 1 3
- = - - - - =
1.( 1).( 7).( 5) 35.
- -
-
0 0 7 28
0 0 0 -
5

36. Đại Số Tuyến Tính å
36
§2: Định Thức
 Hay
1 2 1 3
2 3 1 5
1 6 5 2
3 4 2 7
D
-
=
- -
-
h h h
2 = 2 -2 1
=
-
1 2 1 3
0 - 1 3 -
1
1 6 5 2
3 4 2 7
- -
-
h h h
3= 3+ 1
=
-
1 2 1 3
0 - 1 3 -
1
0 8 4 1
3 - 4 -
2 -
7
4 4 1 h =h -3h
0 2 1 2
- -
1 3 1
. 8 4 1 ...
2 1
= =
1
- -
2

37. Đại Số Tuyến Tính å
37
§2: Định Thức
 Bài tập: Tính định thức
0 2 3 5
1 0 2 2
2 3 0 6
4 1 7 0
D
-
=
-
-
1 0 2 2
0 2 3 5
2 3 0 6
4 1 7 0
-
-
h1«h2
=
h = h +
2
h
3 3 1
h h 4
h
=
= -
4 4 1
-
1 0 2 2
0 2 3 5
...
- =
0 3 4 2
0 1 -
1 8

38. Đại Số Tuyến Tính å
38
§2: Định Thức
 Bài tập: Tính định thức sau
1 1 2 0
3 1 0 4
2 0 5 2
0 3 6 1
D
-
-
=
- -
= ?

39. Đại Số Tuyến Tính å
39
§2: Định Thức
 Ví dụ: Tính định thức cấp n sau
1 1 1 ... 1
1 0 1 ... 1
1 1 0 ... 1
... ... ... ... ...
1 1 1 ... 0
n D =
2 1 h h -=
1 1 1 ... 1
0 -
1 ... 0
1 1 0 ... 1
... ... ... ... ...
1 1 1 ... 0
 Tiếp tục hàng 3 trừ hàng 1, hàng 4 trừ
hàng 1, …

40. Đại Số Tuyến Tính å
40
§2: Định Thức
 Ta được:
1 1 1 ... 1
0 1 0 ... 0
0 0 1 ... 0
... ... ... ... ...
0 0 0 ... 1
n D
-
= -
-
= (-1)n-1

41. Đại Số Tuyến Tính å
41
§2: Định Thức

42. Đại Số Tuyến Tính å
42
§2: Định Thức
 Ví dụ: Cho 2 ma trận
2 3 1 5
A B é ù é ù
= ê ;
= ë 1 4 ú ê ú
û ë 2 7
û
8 31
9 33
AB é ù
Þ = ê ú
ë û
det(A) = 5;det(B) = -3
det(AB) = -15 = 5.(-3) = det(A).det(B)