Chương 5 trình bày các phương pháp tính gần đúng đạo hàm và tích phân xác định trong toán học, đặc biệt khi hàm số không có dạng tường minh. Nó giới thiệu các công thức như Taylor, Newton-Lepnits và Simpson để tính toán gần đúng với các sai số được đánh giá cho từng phương pháp. Các ví dụ cụ thể được đưa ra để minh họa cách áp dụng các công thức này trong thực tế.

1. CHƯƠNG 5 TÍNH GẦN ĐÚNG ĐẠO HÀM VÀ TÍCH PHÂN XÁC ĐỊNH

2. Đặt vấn đề Trong toán học, đã có phương pháp tính đạo hàm và tính phân xác định Thực tế, thường gặp các trường hợp : Hàm y=f(x) chỉ được cho ở dạng bảng, công thức tường minh của y là chưa biết. Hàm f(x) đã biết, nhưng phức tạp Hoặc viết chương trình máy tính để tính tích phân xác định. Chọn giải pháp: “Tính gần đúng”

3. Tính gần đúng đạo hàm

4. Tính gần đúng đạo hàm Áp dụng công thức Taylor: Đặt h = x-x 0   x=x 0 +h: Khi |h| khá bé có thể bỏ qua số hạng có h 2 . Khi đó (5.1) Có thể lấy công thức (5.1) để tính gần đúng f’(x 0 ) khi |h| khá bé

5. Tính gần đúng đạo hàm Sai số: Với |f’’(x)|<=M,  x  [x 0 ,x 0 +h] Ví dụ: Cho f(x)=2x 4 +x-1. Tính f’(1)? Giải: Chọn h=0.001, ta có: Sai số: Do |f’’(x)|≤|f’’(1,001)|=24,05  x  [1;1,001]

6. Tính gần đúng đạo hàm Áp dụng đa thức nội suy Xấp xỉ f(x) bằng đa thức nội suy P n (x), với n+1 mốc a=x 0 <x 1 <x 2 <…<x n =b f’(x)  P n ’(x) với x  [a,b] Sai số:

7. Tính gần đúng đạo hàm Đa thức nội suy Lagrange với 2 mốc nội suy:

8. Tính gần đúng đạo hàm Đa thức nội suy Newton với các mốc cách đều: x i+1 -x i = h Với Lưu ý

9. Tính gần đúng đạo hàm Trường hợp 3 mốc: x 0 , x 1 , x 2 với x 1 -x 0 =x 2 -x 1 = h

10. Tính gần đúng tích phân xác định

11. Tính gần đúng tích phân Cần tính Nếu hàm f(x) liên tục trên [a,b] và có nguyên hàm F(x), công thức Newton – Lepnit: Trường hợp: - f(x) chỉ được cho ở dạng bảng hoặc f(x) - Hoặc f(x) đã biết nhưng tính toán phức tạp  Thay vì tính đúng, tính gần đúng sẽ đơn giản hơn

12. Công thức hình thang Phân hoạch [a,b] thành n đoạn con bằng nhau: x 0 =a<x 1 <…<x n =b x 0 =a b=x n f(x) x 1 x 2 x i X i+1 h=x i+1 -x i =1/n

13. Công thức hình thang Trên đoạn [x i , x i+1 ], xấp xỉ f(x) bởi đa thức (bậc 1) P 1 (x) Đặt x = x i +th  dx = hdt. Với x  [x i , x i+1 ]  t  [0,1] sai số: Với c  [x i , x i +h]

14. Công thức hình thang I i gần bằng diện tích hình thang x i ABx i+1 x i x i+1 f(x) h y i+1 y i r i (h) A B

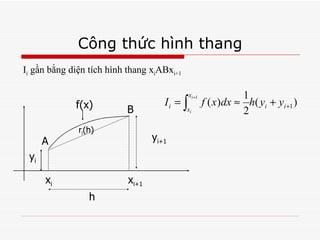
15. Công thức hình thang Công thức hình thang tổng quát: Sai số toàn phần: Với M = sup|f’’(x)| , x  [a,b]

16. Công thức hình thang Ví dụ: Tính gần đúng các tích phân sau bằng công thức hình thang Với phân hoạch [1,5] thành 4 phần bằng nhau. Đánh giá sai số

17. Công thức Simpson Phân hoạch [a,b] thành 2n đọan con bằng nhau: a=x 0 <x 1 <……<x 2n =b x 0 =a b=x 2n f(x) x 1 x 2

18. Công thức Simpson Xét đoạn kép [x i , x i+2 ]. Xấp xỉ f(x) bởi đa thức nội suy bậc 2 P 2 (x): x i X i+1 X i+2 f(x) P 2 (x)

19. Công thức Simpson Sai số: Nếu |f (4) (x)| ≤ M,  x  [x i , x i+2 ] thì: Đặt x = x i + th, dx = hdt; x =x i  t=0; x = x i+2  t=2 =

20. Công thức Simpson toàn phần Sai số tòan phần: Với M thỏa: |f (4) (x)| ≤ M  x  [a,b]

21. Ví dụ và bài tập Dạng 1: Cho trước phân hoạch đoạn [a,b]. Tính gần đúng tích phân và đánh giá sai số Dạng 2:

22. Ví dụ và bài tập Bằng cách phân hoạch đoạn [0,1] thành 4 đoạn bằng nhau, tính gần đúng tích phân trên theo công thức Simpson 1. Cho tích phân: 2. Cho tích phân: Bằng cách phân hoạch [0,1] thành 6 đoạn bằng nhau. Tính gần đúng tích phân đã cho bằng công thức hình thang và công thức Simpson Đánh giá sai số? b) Tính gần đúng tích phân trên bằng công thức hình thang với sai số không quá 3.10 -4