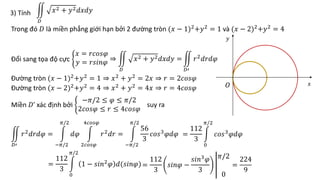
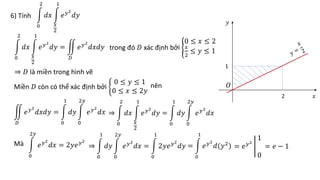
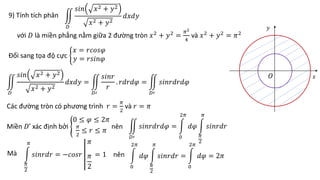
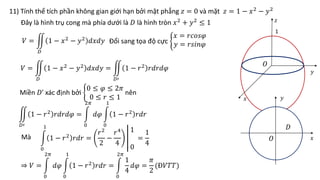
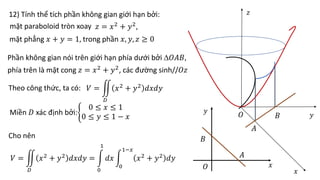
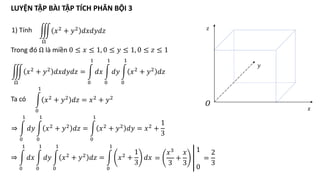
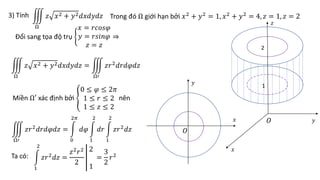
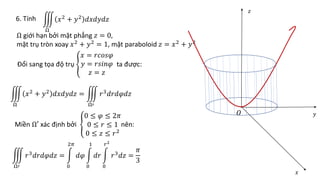
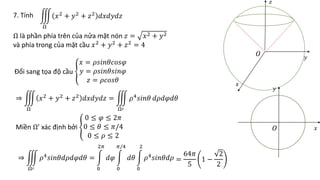
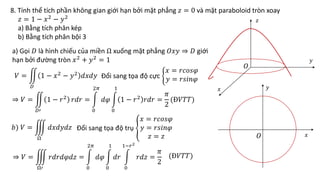
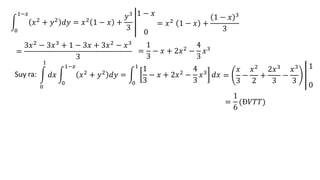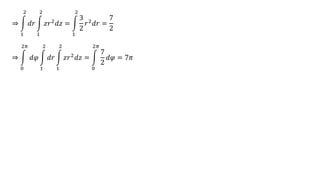Tài liệu hướng dẫn chi tiết các phương pháp tính tích phân kép trong các miền phẳng cụ thể, bao gồm các công thức đổi sang tọa độ cực và các bước tính toán cụ thể. Các bài tập cụ thể từ 1 đến 13 đều đề cập đến các hình dạng miền khác nhau và áp dụng các phương pháp tích phân khác nhau. Ngoài ra, tài liệu cũng đề cập đến ứng dụng trong việc tính diện tích và thể tích của các hình khối không gian.