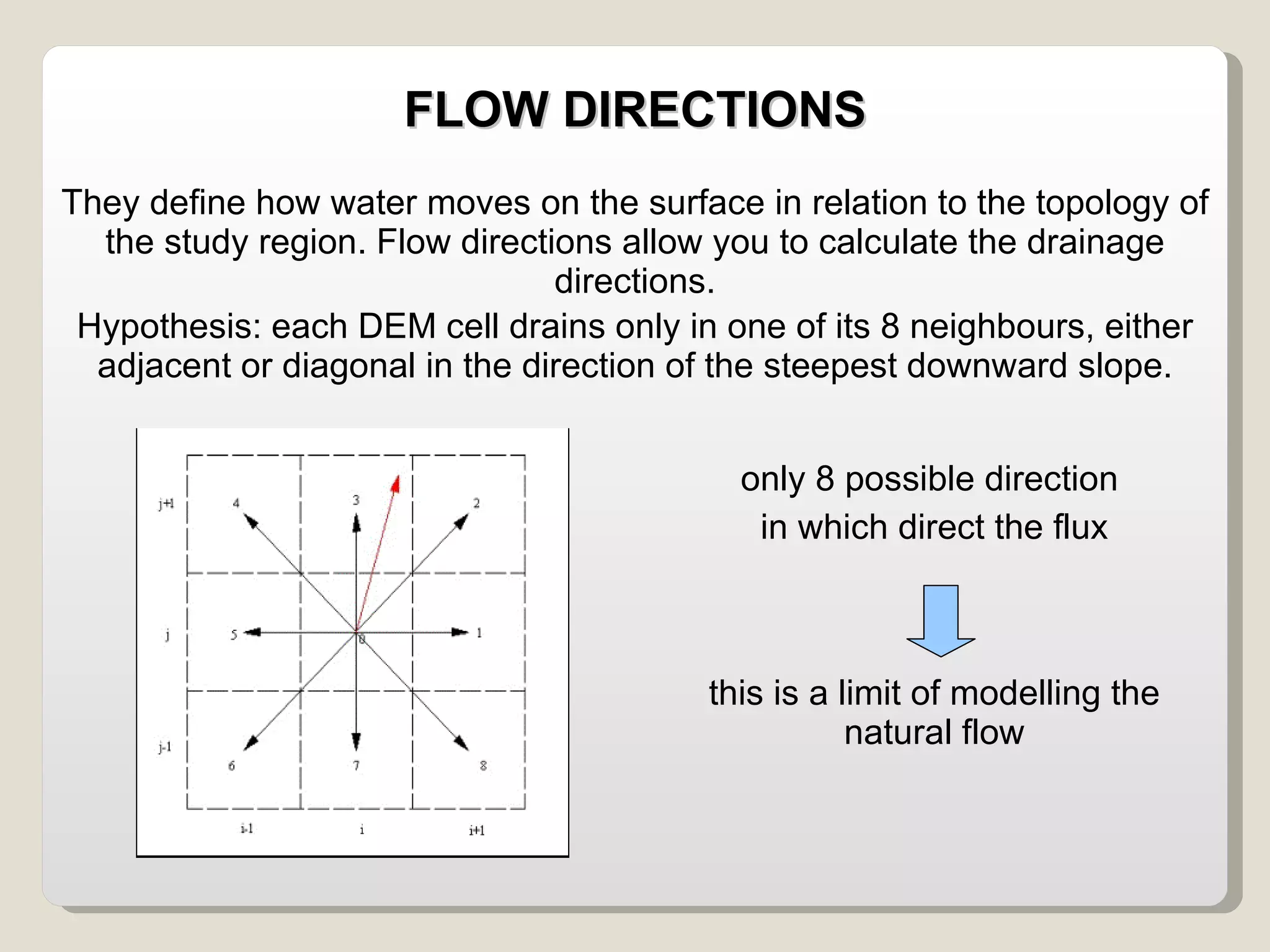
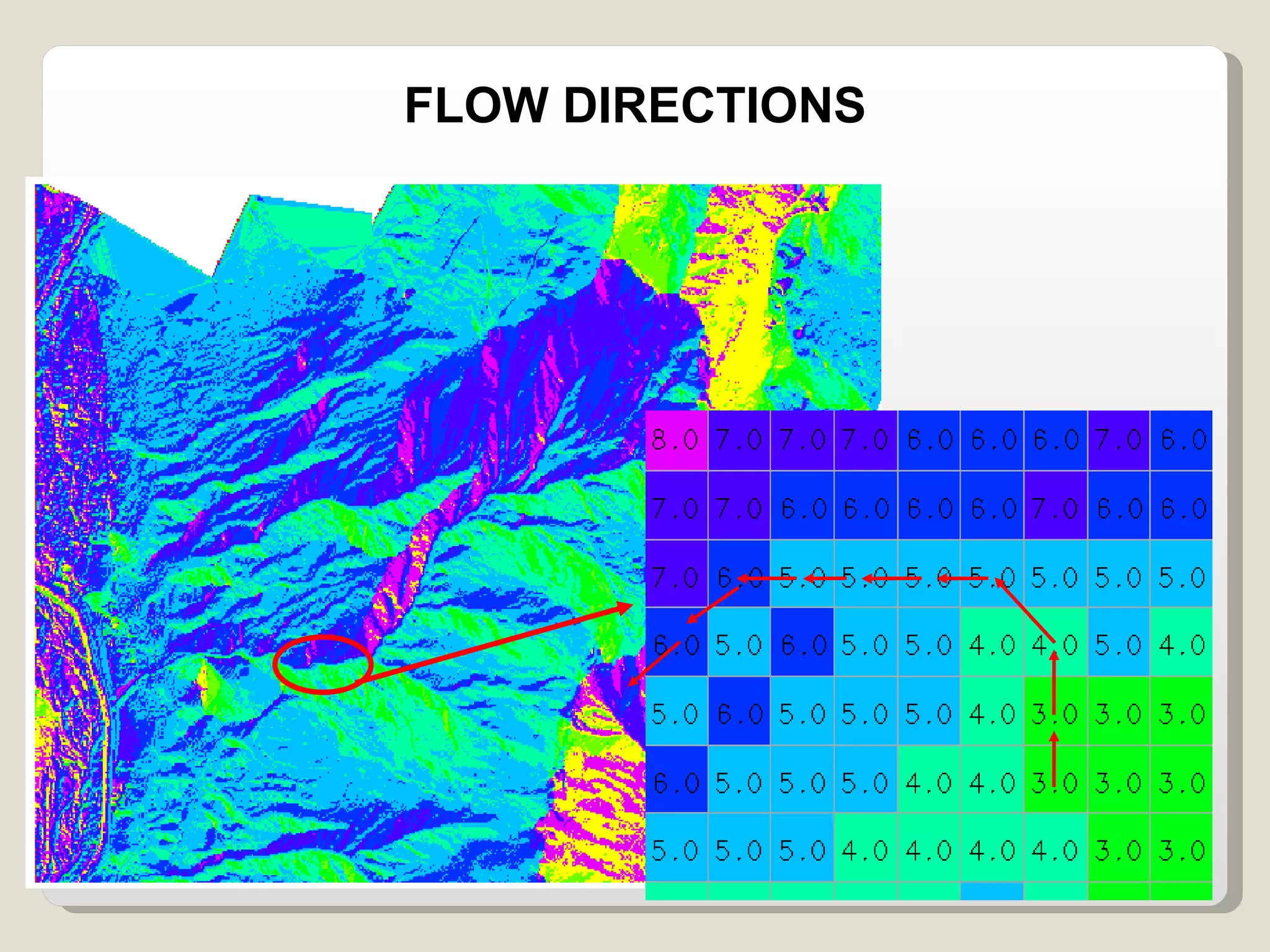
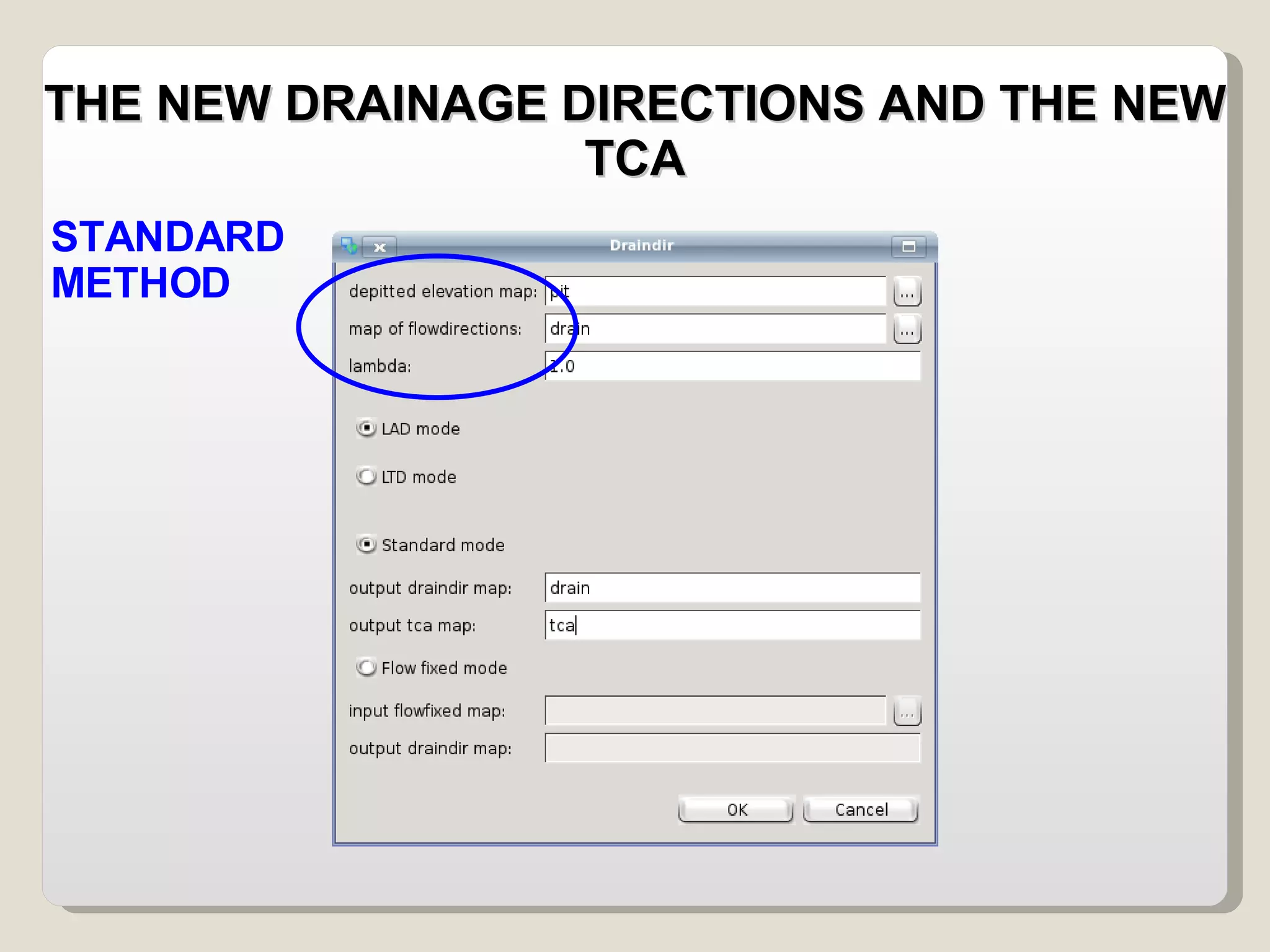
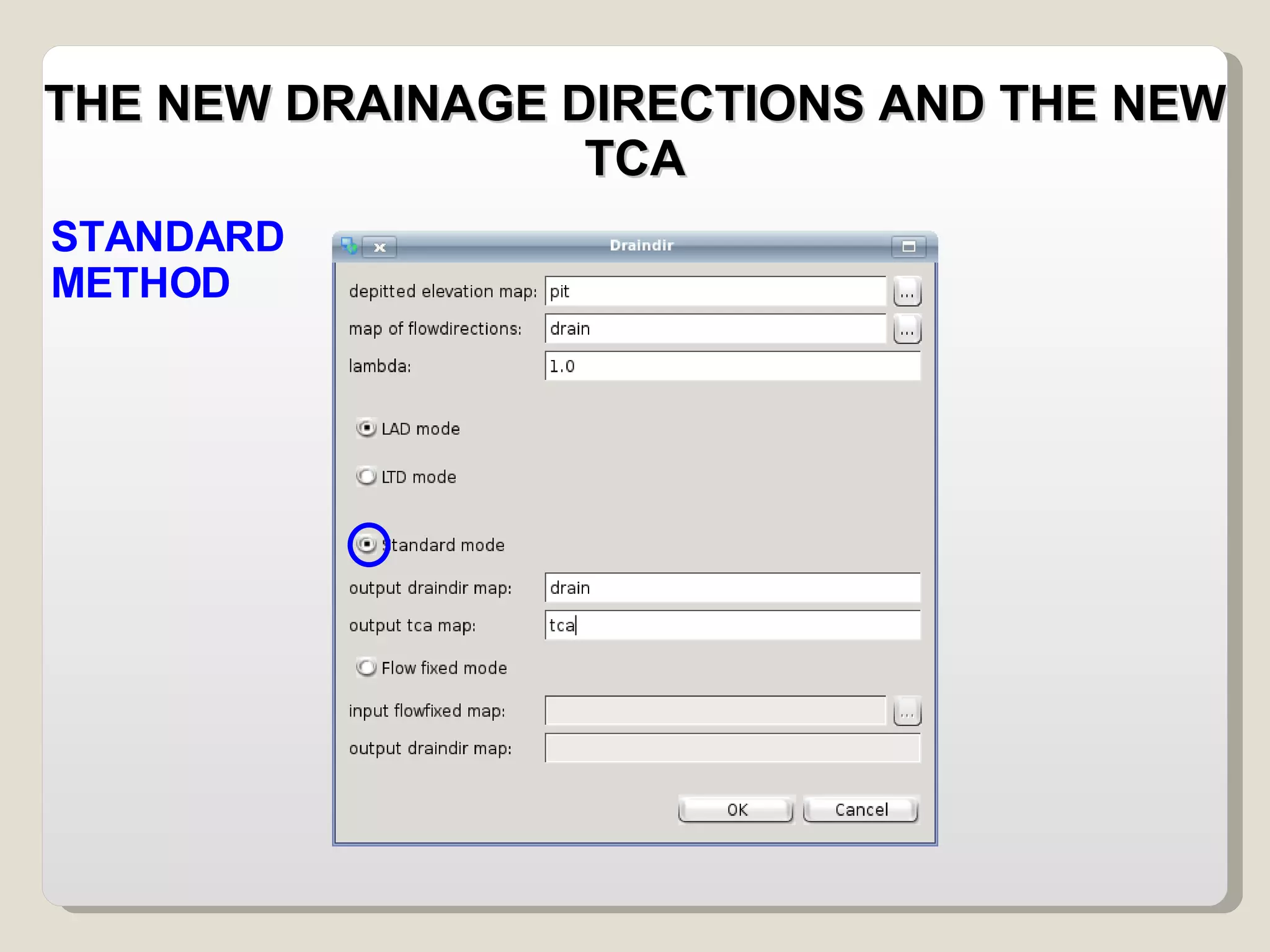
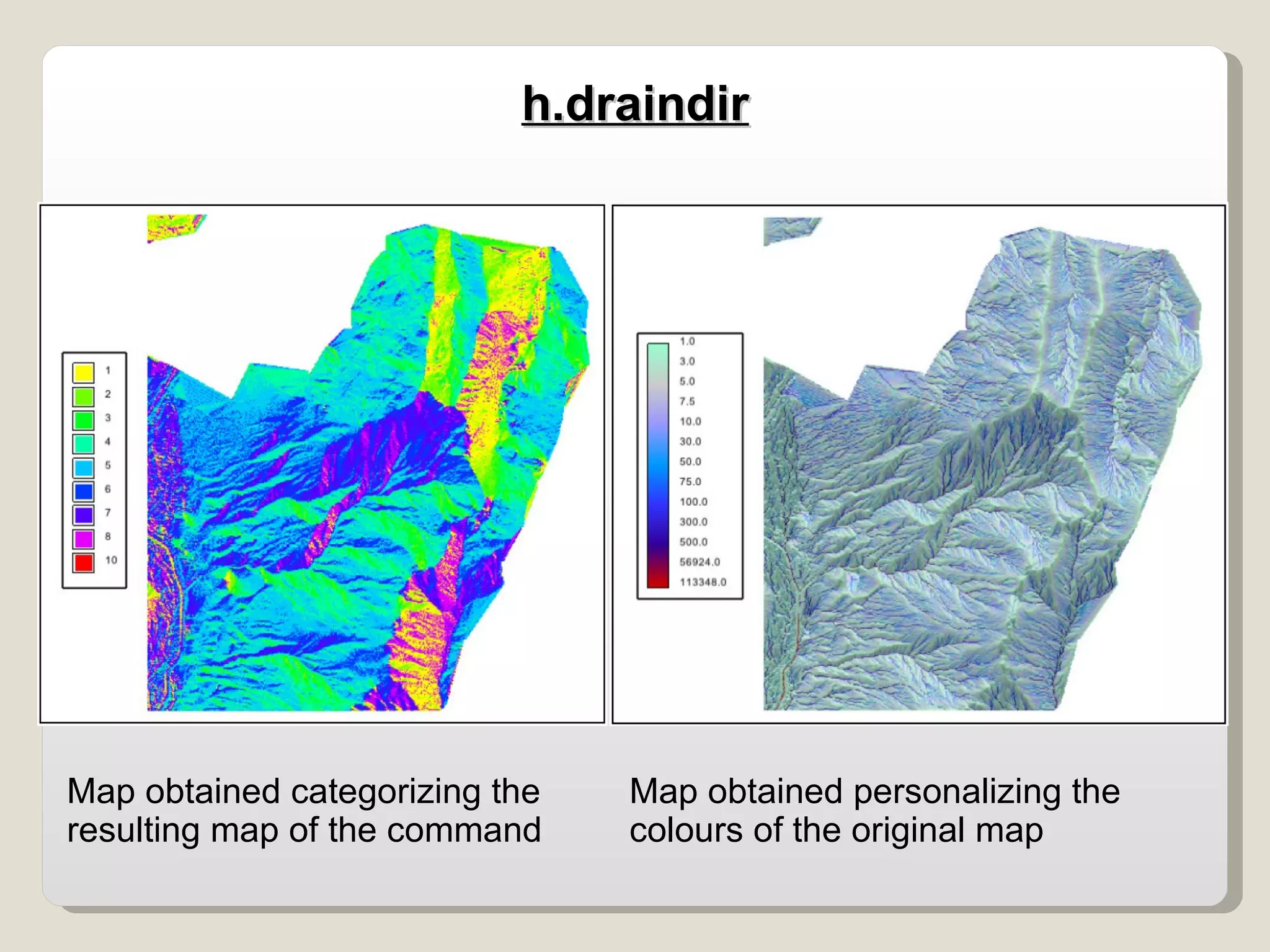
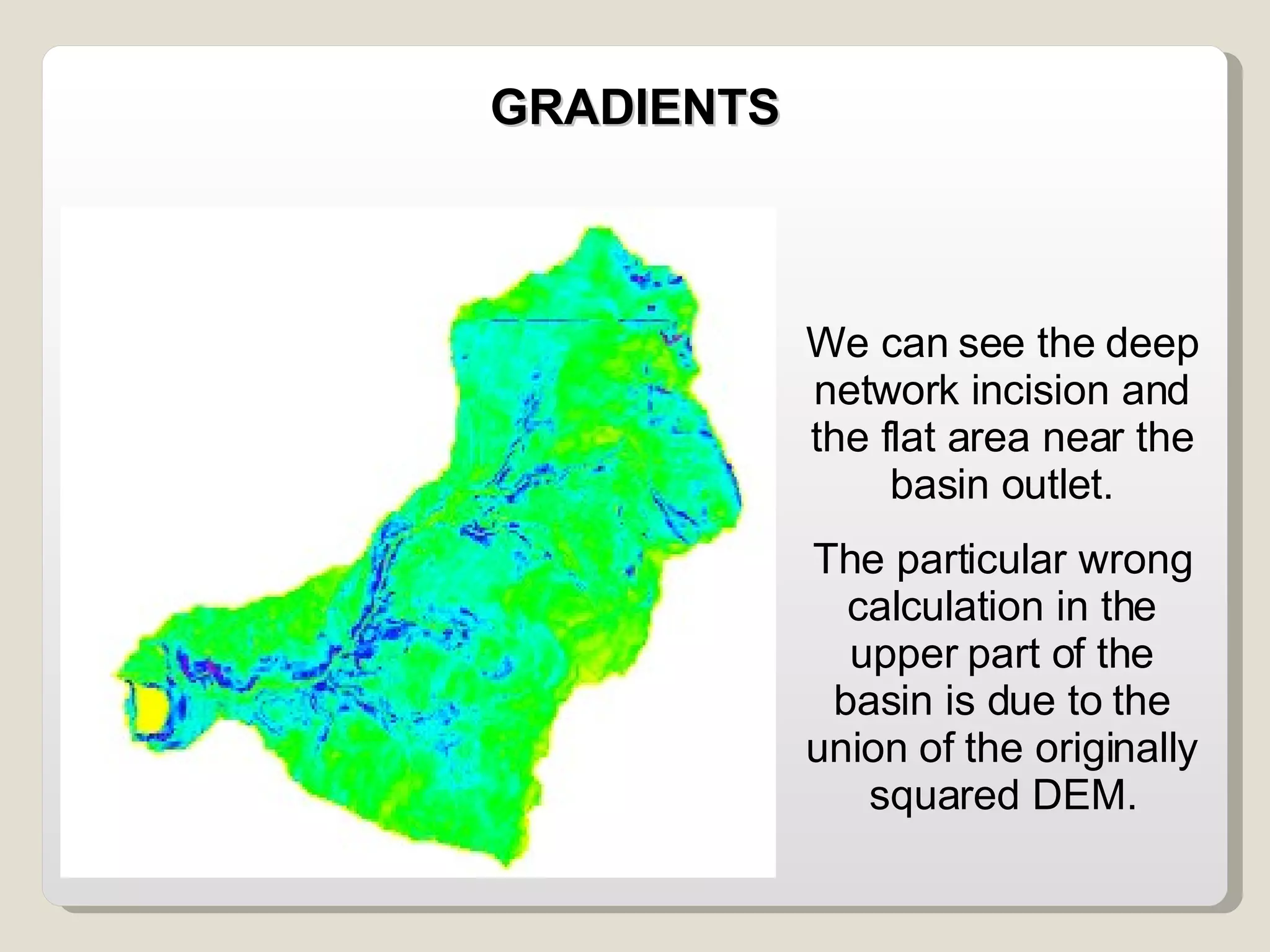
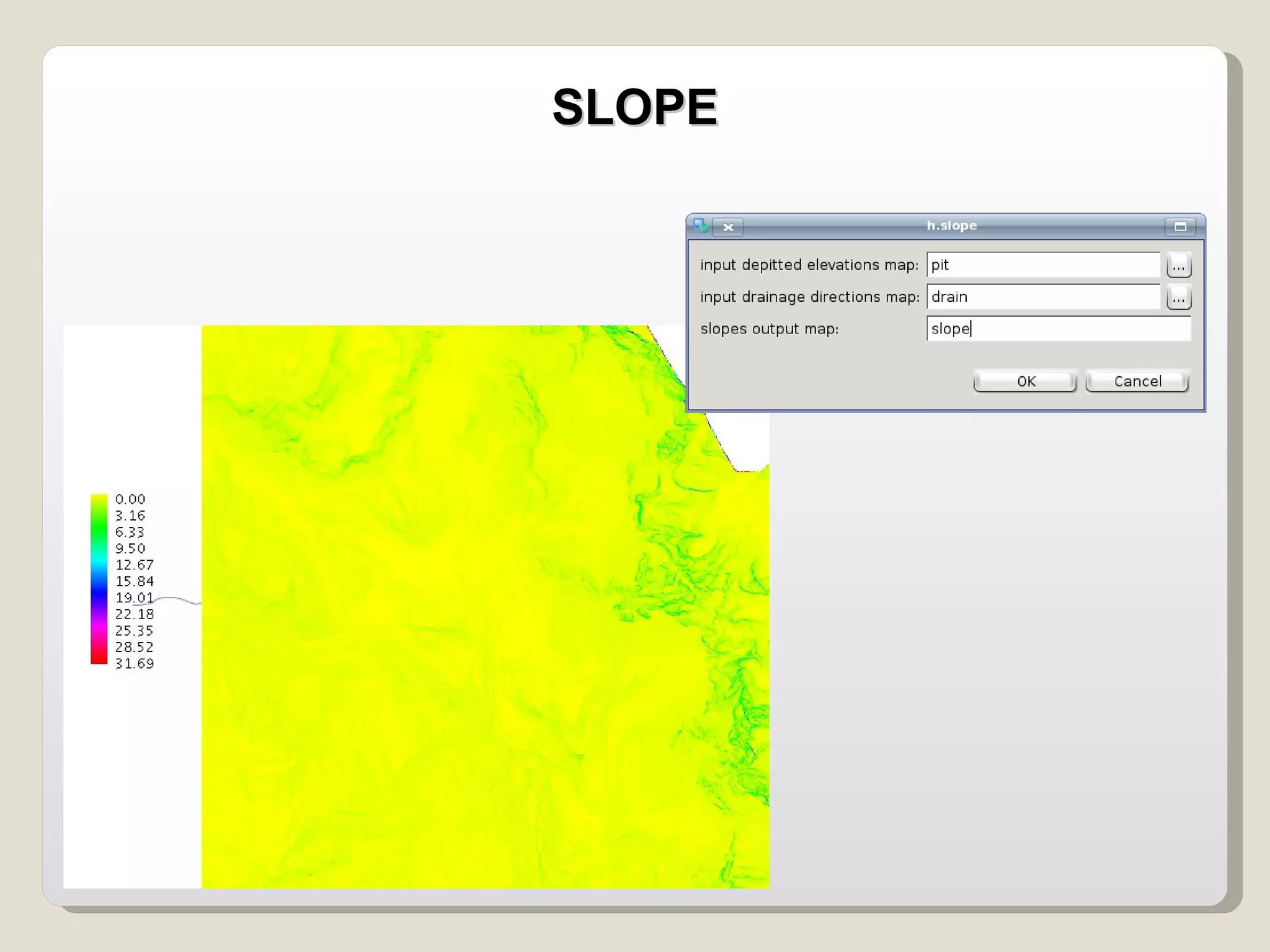
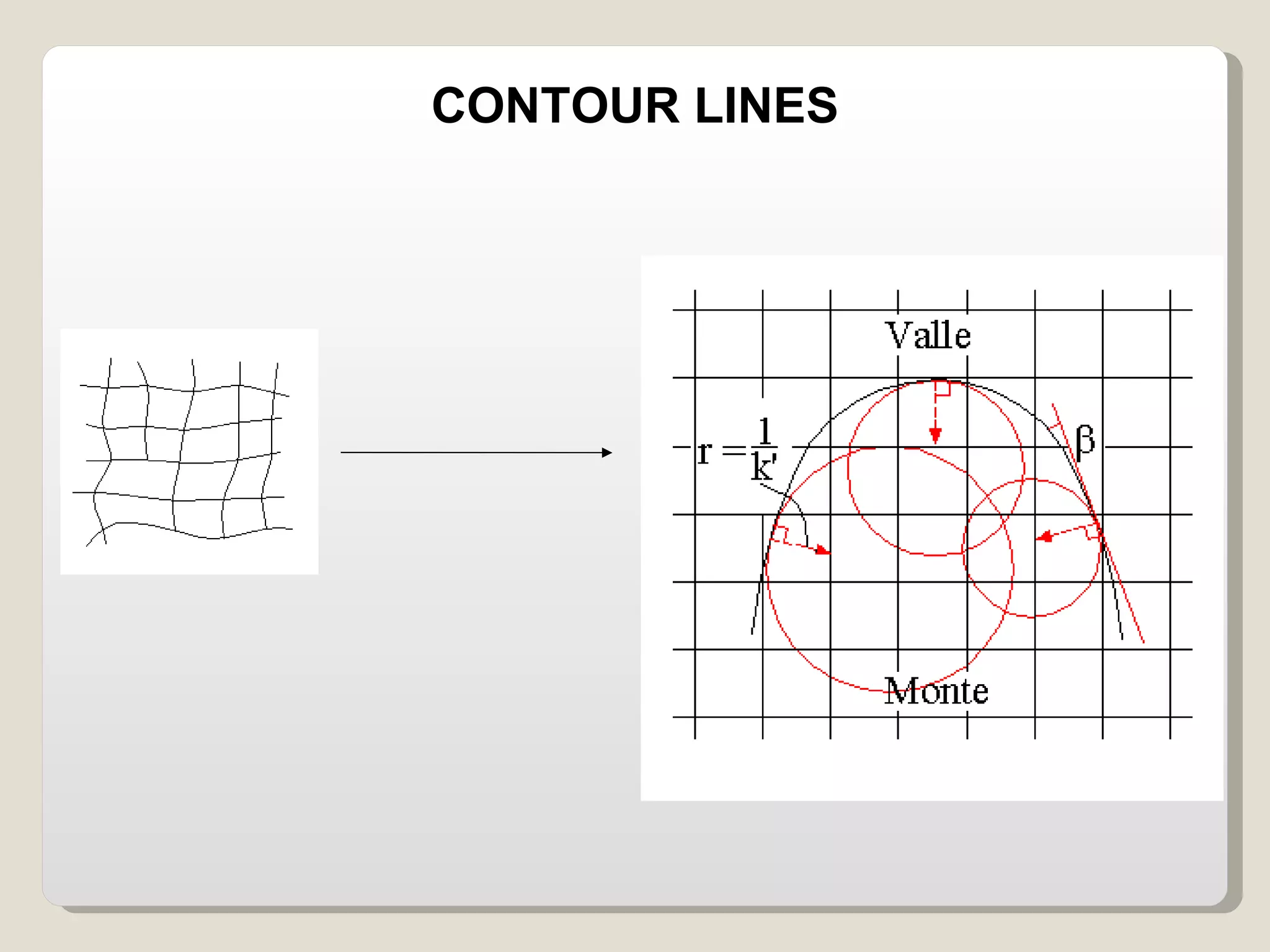
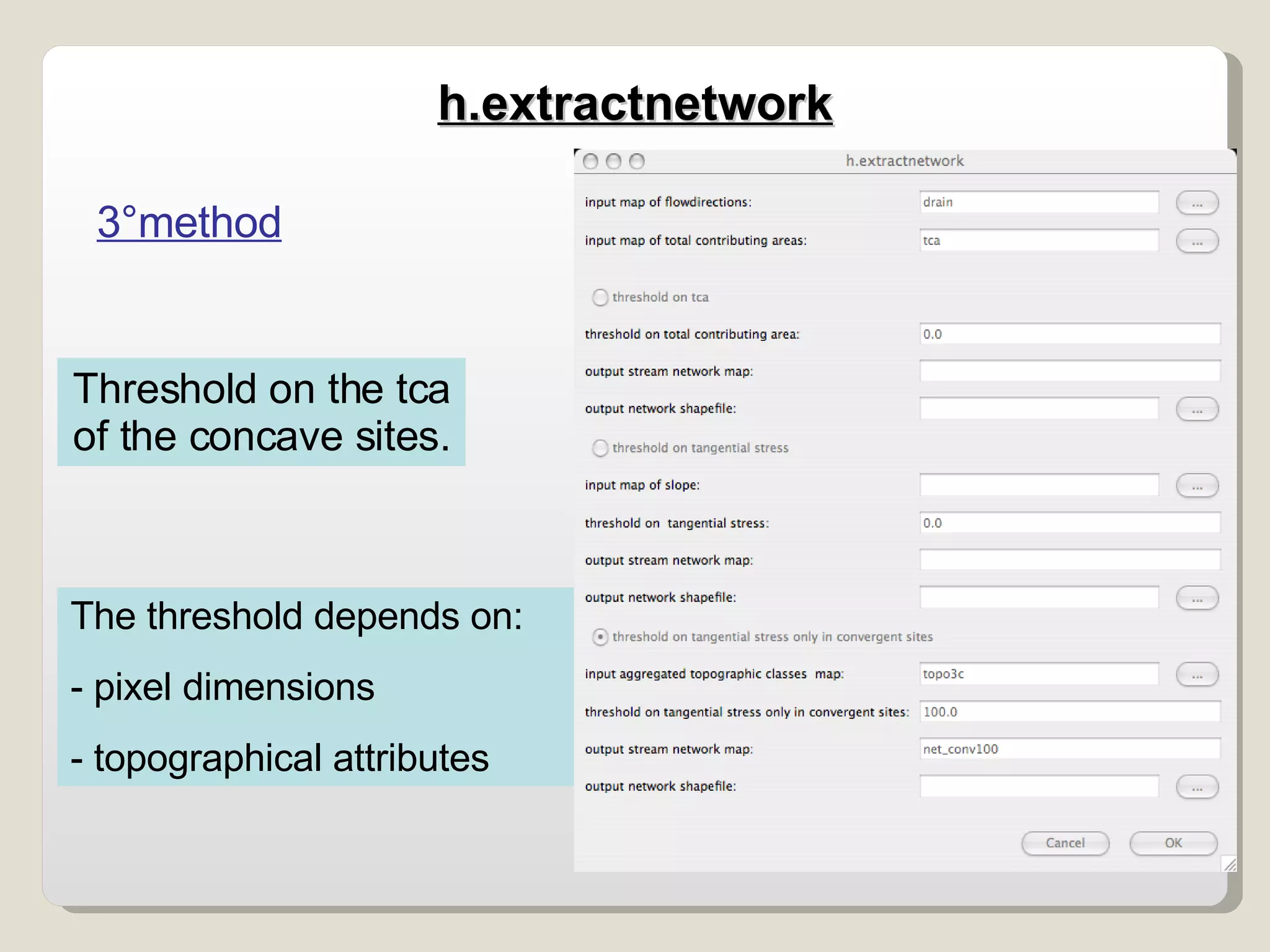
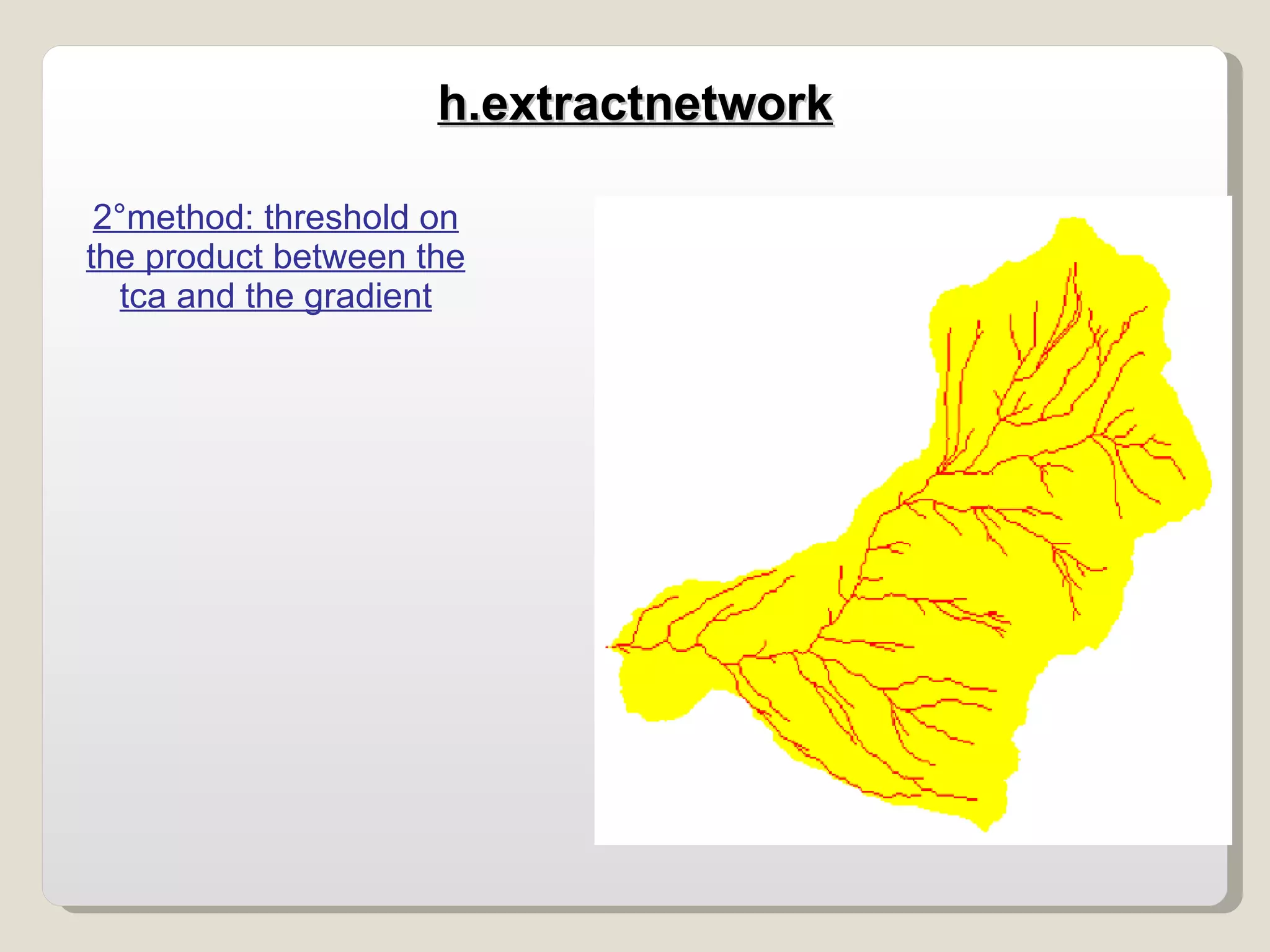
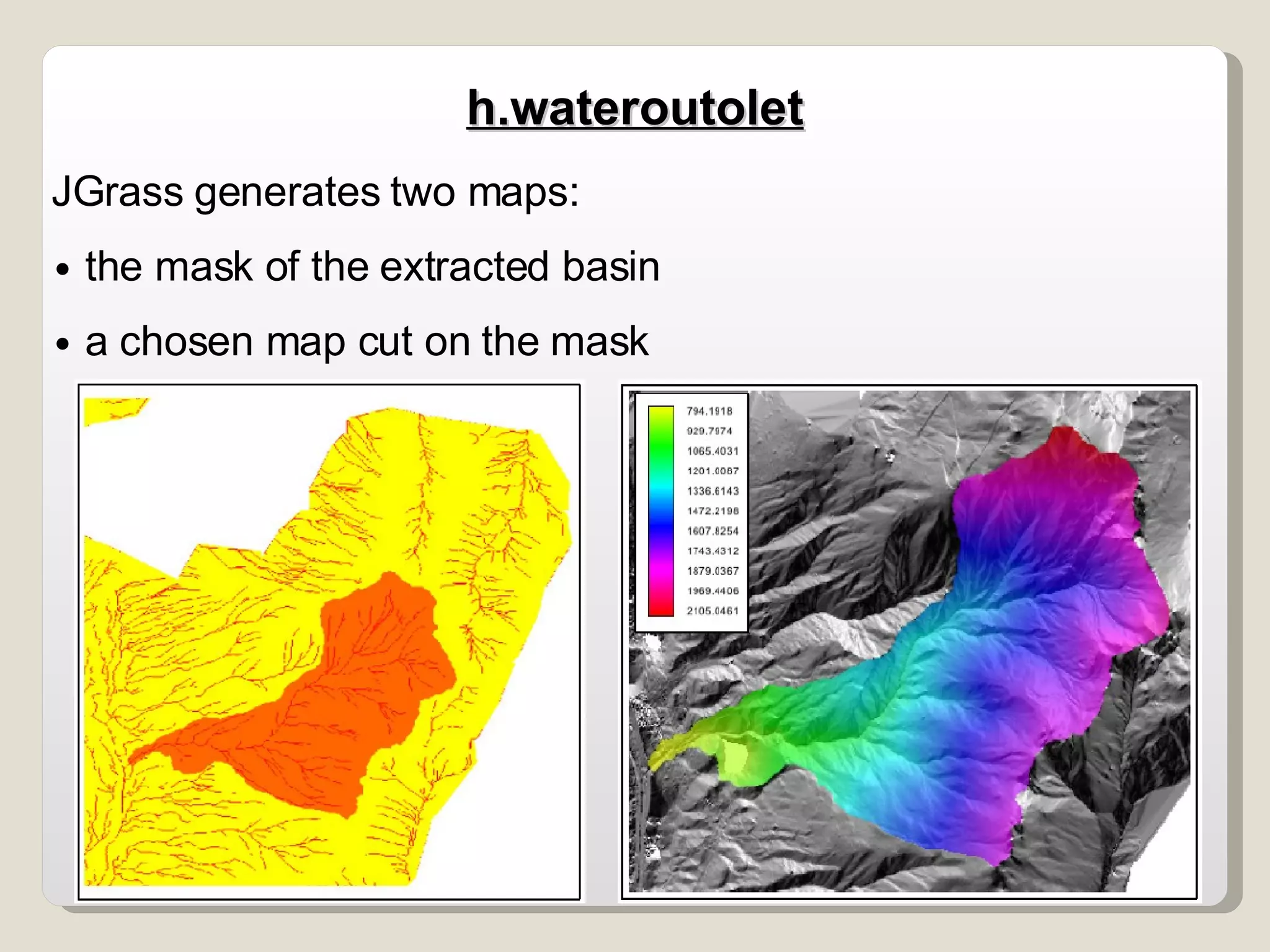
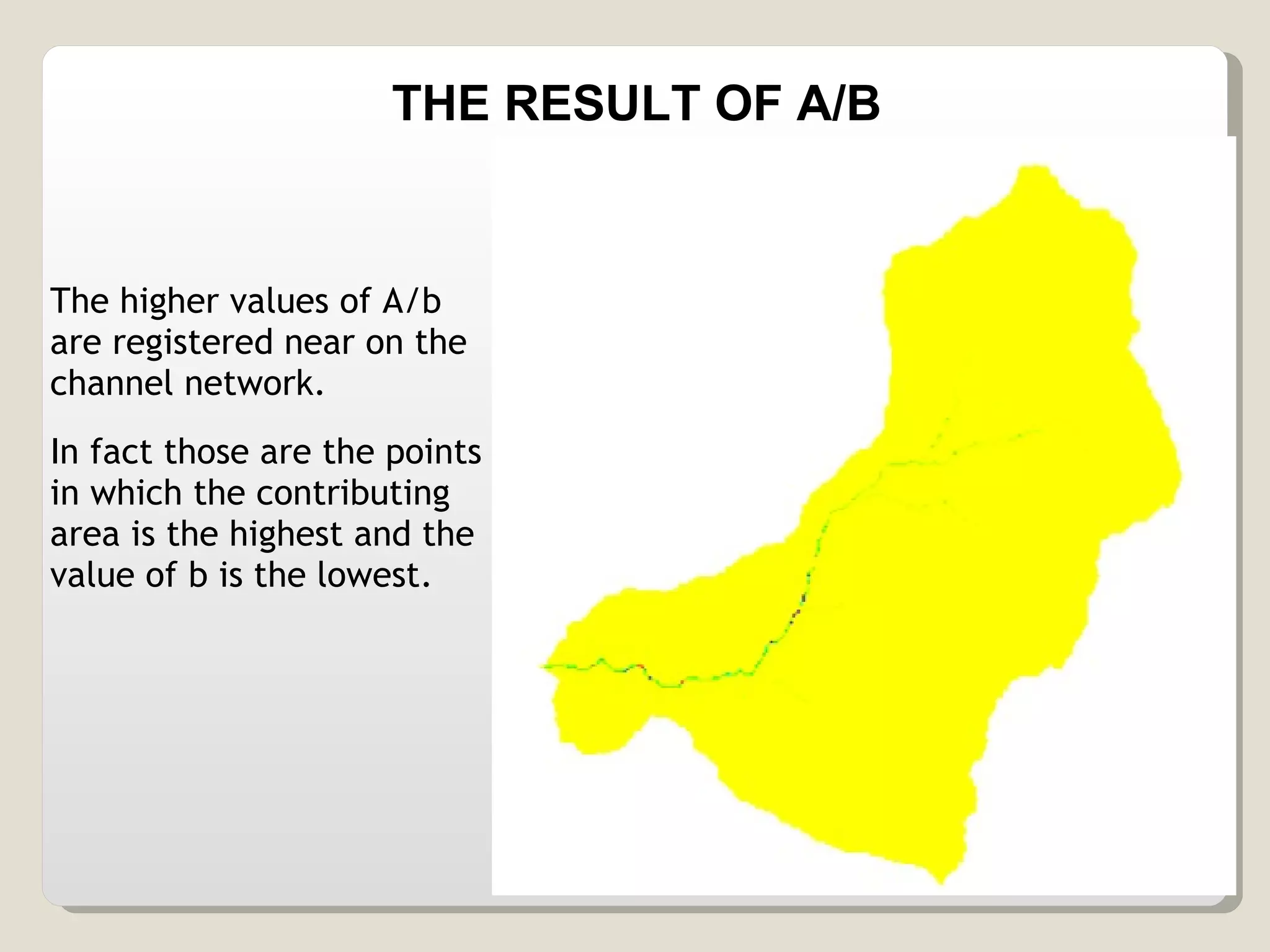
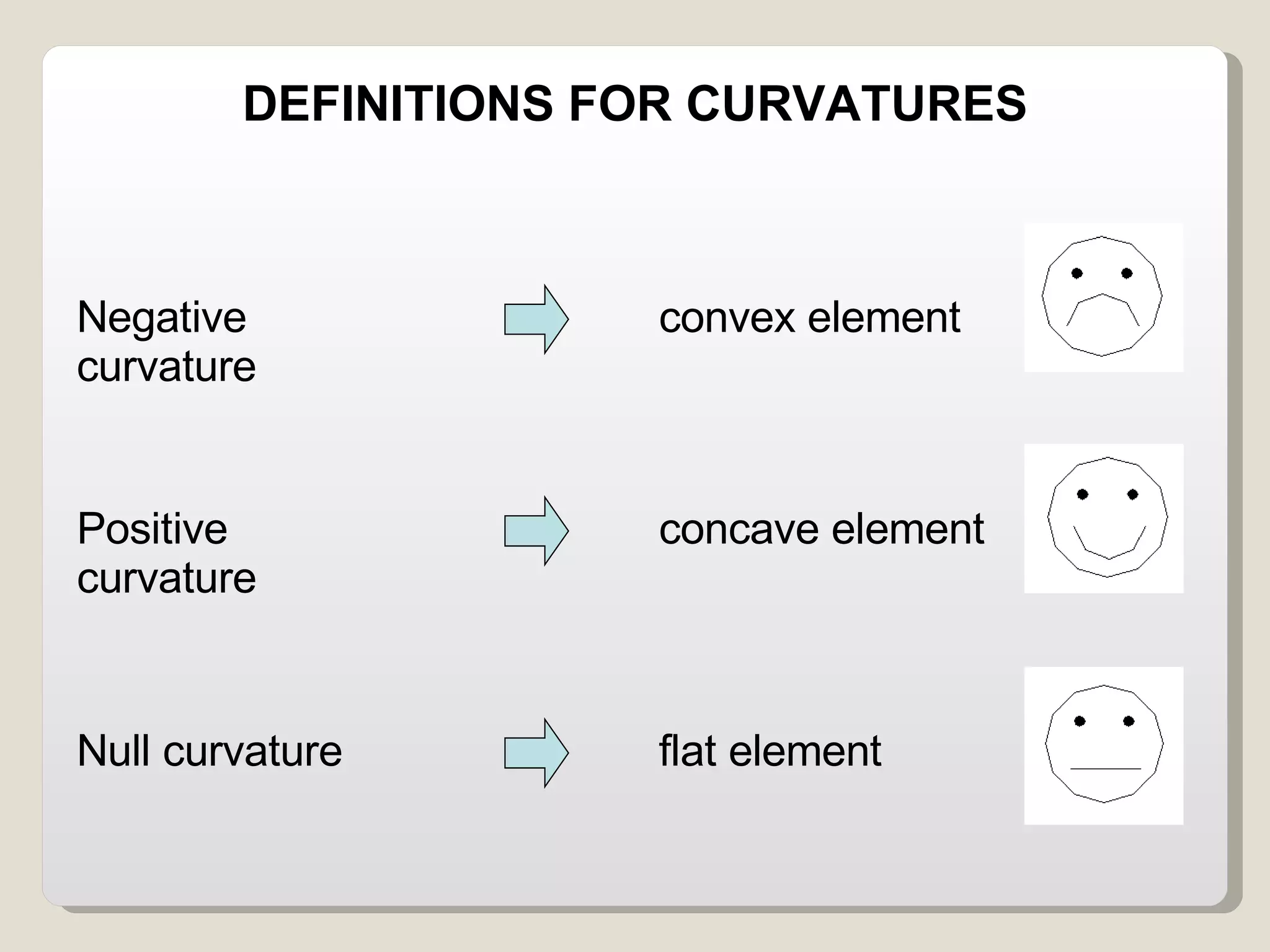
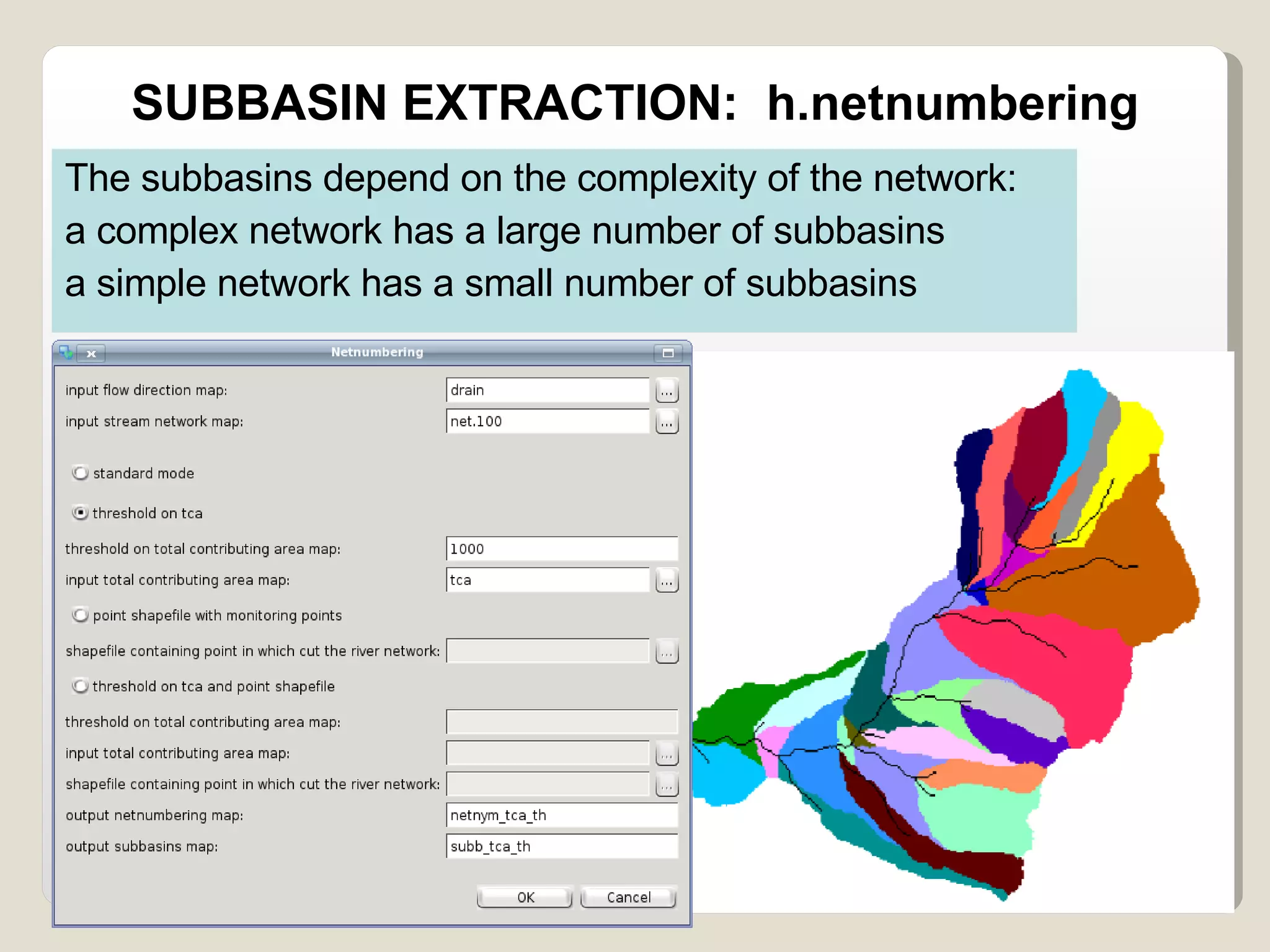
The document discusses various geomorphological analysis tools available in the open-source software HortonMachine. It describes how HortonMachine can be used to analyze digital elevation models (DEMs), calculate terrain attributes, extract stream networks, and delineate catchment boundaries. Specific commands are mentioned for calculating flow directions, drainage networks, slope, curvature, catchment attributes and more. The goal is to provide quantitative and qualitative tools for understanding catchment morphology.