Remote Sensing & GIS based drainage morphometry

I | P a g e
A Seminar Report
On
GIS Based Drainage Morphometric Analysis
Submitted in partial fulfilment for the
Degree of Master of Technology in
Geoinformatics and Natural Resource Engineering
Submitted by
Akshay D. Wakode
Roll No. 163310023
Under the guidance of
Prof. M.V Khire
Centre of Studies in Resource Engineering
Indian Institute of Technology, Bombay
Powai, Mumbai, Maharashtra
India, 400076
April, 2017

II | P a g e
Approval Sheet
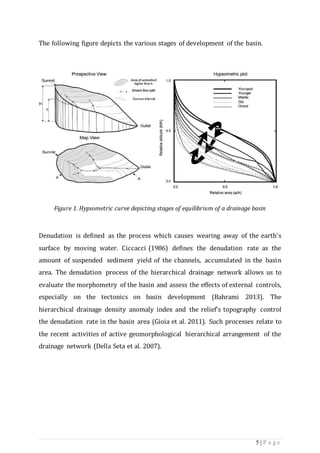
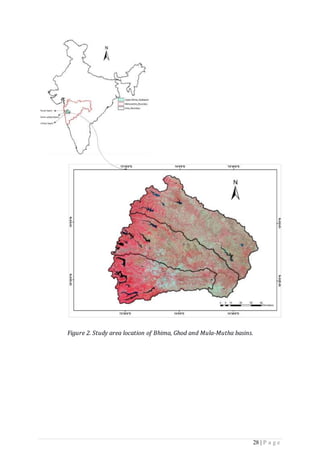
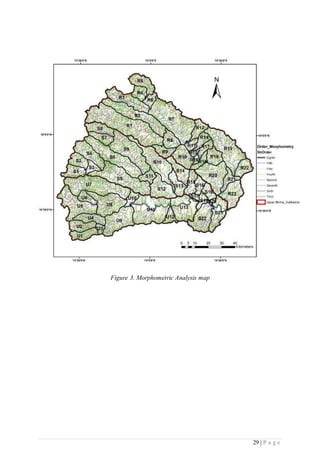
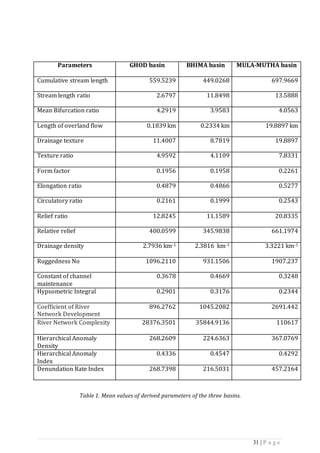
This seminar report entitled “GIS based Drainage Morphometric Analysis”
prepared by Akshay D. Wakode (Roll No. 163310023) is hereby approved
for submission.
Guide
Prof. M.VKhire
Date:

III | P a g e
Declaration
I declare that this written submission representsmy ideasin my own words
andwhereothers ideasor wordshavebeen included,Ihaveadequately cited
and referenced the original sources. I also declare that I have adhered to all
principles of academic honesty and integrity and have not misrepresented
or fabricated or falsified any idea/data/fact/source in my submission. I
understand that any violation of the above will be cause for disciplinary
action by the Institute and can also evoke penal action from the sources
which have thus not been properly cited or from whom proper permission
has not been taken when needed.
Akshay D. Wakode
M.Tech (1st Year), CSRE, IIT Bombay

I | P a g e
Abstract
Remotesensingand GeographicalInformation Systems(GIS)techniques are
increasingly being used for morphometric analysis of drainage basins
throughoutthe world.GISfacilitates the manipulationandanalysisof spatial
information obtained usingremotesensing. Integrating GIS and RSprovides
an efficient mechanism not only to upgrade and monitor morphometric
parameters but also to permit spatial analysis of other associated thematic
database. As compared to the conventional morphometric studies, remote
sensing providesextant ground reality inputs to assess changes in drainage
patterns, density soil characteristics and land-use/land form changesin real
life. Satellite image and aerial photographsprovideavery good inputsource
for the preparation of thematic layers. Morphometric evaluation in
conjunction with high resolution satellite data, in different geological and
climatic conditions, help in the better understanding of the status of
landformsand their processes, along with indications about the soil and its
erosion, drainage management and evaluation of groundwater potential
conditions for watershed planning and efficient management. Remotely
sensed images provideinformation on the surface character of the terrain,
which are further exploited to derive the subsurface expressions. This as a
whole finds extensive application in various civil engineering projects and
geological studies.

II | P a g e
Contents
Abstract ................................................................................................................................... I
List of figures ...................................................................................................................... III
List of tables........................................................................................................................ III
Abbreviations.......................................................................................................................IV
1. Introduction................................................................................................................... 1
1.1 What is Morphometry?........................................................................................ 1
1.2 RS and GIS in morphometry .............................................................................. 3
2. Drainage Morphology.................................................................................................. 4
2.1 Morphometric Parameters................................................................................. 6
2.1.1 Linear aspects.................................................................................................15
2.1.2 Areal aspects....................................................................................................19
2.1.3 Relief aspects...................................................................................................24
3. Case Study.....................................................................................................................27
4. Results & Discussion..................................................................................................32
4.1 Estimating dominant parameters ..................................................................32
4.2 Further application.............................................................................................37
References ...........................................................................................................................38

III | P a g e
List of figures
Figure 1. Hypsometric curve depicting stages of equilibrium of a drainage basin
................................................................................................................................................... 5
Figure 2. Study area location of Upper Bhima, Ghod and Mula-Mutha basins....28
Figure 3. Correlation matrix of morphometric variables for GHOD basin............33
Figure 4. Correlation matrix of morphometric variables for BHIMA basin..........34
Figure 5. Correlation matrix of morphometric variables for MULA-MUTHA basin
.................................................................................................................................................35
List of tables
Table 1. Mean values of derived parameters of the three basins. ...........................31

IV | P a g e
Abbreviations
DEM Digital ElevationModel
RS Remote Sensing
GIS Geographical InformationSystem

1 | P a g e
1. Introduction
Water is a compound of paramount importance. The demand for water is growing
as the world’s population is increasing and rapid urbanization is taking place
worldwide. On the other hand, water resources are limited. Increasing demand for
various uses along with decreasing access to good quality water as nearby good-
quality sources have already been overexploited, just aggravates the condition.
Urban sprawling and population growth in countries like India, leads to an
increase in the stress on existing water resources, because of growing demands
for drinking, irrigation and industrial needs [Singh et al. 2011]. Such an increase
in the usage of water has affected both surface and groundwater supplies,
resulting in an acute water crisis [Thakur et al. 2011]. In addition, low-intensity
and erratic monsoons create further shortages of surface-water supply. As a result,
the demand for groundwater resources has increased tremendously year by year,
causing a drastic decline in its levels. Overexploitation of groundwater has led to
the drying up of the aquifer zones in several parts of the country. Around 70% of
the country’s population is directly or indirectly dependent upon agriculture
based economy, and adequate availability of good-quality water is a prerequisite
for it [Usha Chirala, 2012]. Hence, it is imperative that optimal utilization of water
resources is a key to the sustenance of future economy [Usha Chirala, 2012].
1.1 What is Morphometry?
Rivers and their tributaries are the key features of a drainage basin. Morphometry
in principle is the measurement and mathematical analysis of the configurations
of the Earth’s surface and the shape and dimensions of its landforms [Clarke,
1966]. It is a modern analytical-cartographic approach to represent bare earth

2 | P a g e
topography by the computer manipulation of terrain height. The form and
structure of the drainage basin along with their associated drainage networks are
described by their morphometric parameters. Quantitative morphometric
measurement is performed using defined mathematical equations, under three
aspects: (1) Linear (2) Areal and (3) Relief.
In the linear aspect of analysis, the linear structures such as length of the main
channel, stream hierarchical orders, bifurcation ratio, length of overland flow,
stream length ratio and mean length of streams are measured to evaluate the
linear morphometric characteristics of the sub-basins. In the areal aspect, sub-
basin area, drainage density, stream frequency, circulatory ratio, elongation ratio,
form factor, drainage texture, texture ratio and constant of channel maintenance
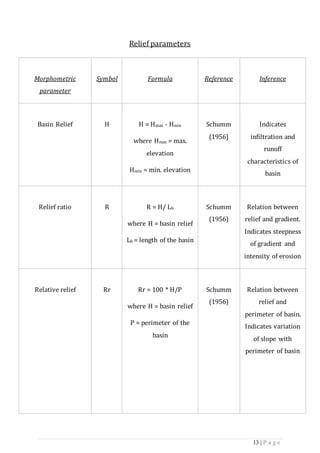
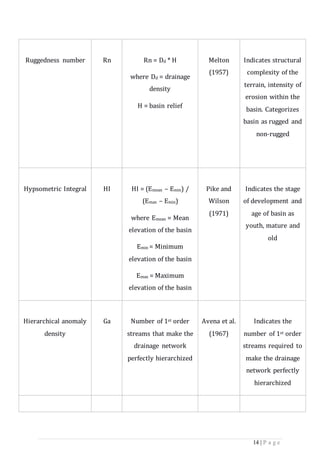
are measured. Relief ratio, relative relief, ruggedness number, hypsometric
integral, hierarchical anomaly density, hierarchical anomaly index, denudation
rate index, coefficient of river network development and river network complexity
are estimated under the relief aspect. Information on the hydrological nature of
the rocks getting exposed within the drainage basin can be obtained by assessing
the characteristics of the drainage basin using quantitative morphometric
analysis.
Geometry of the drainage basin is the result of numerous factors which reshape
the topography of the region over a period of time. All these factors influence the
surface run-off, water discharge and also the nature of the drainage pattern of
stream channels in the basin. The factors include climate, topography, bedrock
type, soil type, and vegetation cover. A proper understanding of these elements
gives insights into the characteristics of sediment discharge and water resource
availability. While it is essential to assess, record and measure these elements
qualitatively and quantitatively, it may not be easy to do that directly all the times
[Usha Chirala, 2012].
In such scenario, a quantitative analysis of drainage basin morphometry provides
a bottom-up approach to unravel the influence and magnitude of the factors

3 | P a g e
responsible for the outcomes. On the other hand, such a study of the drainage
morphometry also plays an important role in understanding the landform
processes, physical properties of the soil and erosion characteristics pertaining
within the basin area.
1.2 RS and GIS in morphometry
Remote sensing and Geographical Information Systems (GIS) techniques are
increasingly being used for morphometric analysis of drainage basins throughout
the world. Remotely sensed images provide a synoptic view of the terrain, and
facilitates the monitoring and analysis of spatial information, obtained using
remote sensing. Integrating GIS and RS provides an efficient mechanism not only
to upgrade and monitor morphometric parameters but also to permit spatial
analysis of other associated thematic database [Jain et al. 1995]. Satellite image
and aerial photographs provide a very good input source for the preparation of
thematic layers.

4 | P a g e
2. Drainage Morphology
Hydrological parameters such as the stream frequency, bifurcation ratio,
circulatory ratio and the length of overland flow of the sub-basin area are dealt
with in the morphometric analysis, which influence the local morphologic
landforms and act as indicators of the structural influence in drainage
development. In many studies such an analysis has been used to assess the
groundwater potentiality of the basins and to locate suitable sites for construction
of check dams and artificial recharge structures. The application of quantitative
techniques in studying drainage basins dates back to 1932, undertaken by Horton
et al. with the use of topographic maps. Hydro-geomorphological studies of
various basins in India considering the linear, areal and relief aspects has been
carried out by the National Institute of Hydrology (1993). Parameters for all
aspects can be derived from DEM datasets using automated GIS operations which
is fast, less subjective and provides more reproducible measurements.
Hypsometry finds the relation between the horizontal cross-sectional area of the
catchment and its elevation (Strahler, 1952). A hypsometric curve/plot provides
relation between the relative height (h/H) and relative areas (a/A) of the basin, ‘h’
being the height of contour, ‘H’ the relief of the basin, ‘a’ the cross-sectional area of
the contour and ‘A’ being the total area of basin. The curve and associated integral
values of the catchment depict the erosional pattern, topographical conditions and
the stage of equilibrium of the basin. These curves are generated using the spatial
analyst module of GIS software (Sarangi et al. 2001). Strahler (1952) and Schumm
(1956) stated that the hypsometric curve represents the stages of the basin and
categorizes them as youth, mature and old.

5 | P a g e
The following figure depicts the various stages of development of the basin.
Figure 1. Hypsometric curve depicting stages of equilibrium of a drainage basin
Denudation is defined as the process which causes wearing away of the earth’s
surface by moving water. Ciccacci (1986) defines the denudation rate as the
amount of suspended sediment yield of the channels, accumulated in the basin
area. The denudation process of the hierarchical drainage network allows us to
evaluate the morphometry of the basin and assess the effects of external controls,
especially on the tectonics on basin development (Bahrami 2013). The
hierarchical drainage density anomaly index and the relief’s topography control
the denudation rate in the basin area (Gioia et al. 2011). Such processes relate to
the recent activities of active geomorphological hierarchical arrangement of the
drainage network (Della Seta et al. 2007).

6 | P a g e
2.1 Morphometric Parameters
Primary measurements such as stream number, stream length, sub-basin area,
sub-basin width, sub-basin elongated distance and the sub-basin perimeter are
derived from the thematic layers and are used to evaluate the different parameters
governing the complex morphometric characteristics of each sub-basin.
Linear parameters
Morphometric
parameter
Symbol Formula Reference Inference
Stream Number Nu Number of stream
segments
Strahler
(1952)
Defines drainage
pattern within
the basin
Stream Order U Hierarchical rank Strahler
(1952)
Defines drainage
pattern within
the basin

7 | P a g e
Stream length (km) Lu Length of the stream
segment
Horton
(1945)
Indicates
variation in
gradient &
texture of the
basin
Mean stream length Lsm Lsm = ∑Lu/Nu
where ∑Lu = total
stream length of order
‘u’
Nu = total number of
stream segments of
order ‘u’
Strahler
(1964)
Depicts changes
in elevation and
area of the basin.
Increases with
the stream order
Stream length ratio RL RL = ∑Lu/Lu1
where ∑Lu = total
‘u’
Lu1 = total stream length
of its next lower order
Horton
(1945)
Indicates
variations in
slope and
topography

8 | P a g e
Bifurcation ratio Rb Rb = Nu/Nu+1
where Nu = total number
of stream segments of
order ‘u’
Nu+1 = total number of
stream segments of its
next higher order
Schumm
(1956)
Indicates
structural
control and
complexity in
drainage pattern,
shape of the
basin
Mean Bifurcation ratio Rbm Average of bifurcation
ratios of all orders
Strahler
(1964)
Indicates shape
of the basin
Length of overland flow Lg Lg = 1/(2 Dd)
where Dd = drainage
density
Horton
(1945)
Indicates
infiltration
capacity and
runoff

9 | P a g e
Areal parameters
Morphometric
parameter
Drainage density
(km/km2)
Dd Dd = ∑Lu/A
where ∑Lu = total
A = area of the basin
Horton
(1932)
Indicates
distribution of
stream segments,
topography, soil
property, relief,
vegetation cover
and infiltration
capacity
Stream frequency
(km/ km2)
Fs Fs = Nu/A
where Nu = total
number of streams of
all orders
A = area of the basin
Horton
(1932)
Represents the
amount of
structural
disturbances
within the basin,
which indicate
amount of surface
runoff and stream
flow

10 | P a g e
Form factor Ff Ff = A/Lb2
where A = area of the
basin
Lb = length of the basin
Horton
(1932)
Describes the
shape of the
catchment area,
peak flow from the
basin
Circulatory Ratio Rc Rc = 4*Pi*A/P2
basin
P = perimeter of the
basin
Miller
(1953)
Indicates shape of
the sub-basin in an
elongated circle.
Influences the
length and
frequency of
streams, geology,
land use/land
cover, climate,
relief and slope
Elongation Ratio Re Re = (2/ Lb) * (A/Pi)0.5
basin
Strahler
(1956)
Indicates shape of
the sub-basin area,
Circular (>0.9)
Oval (0.9-0.8)

11 | P a g e
Less elongated
(<0.7)
Drainage texture T T = Dd * Fs
where Dd = drainage
density
Fs = stream frequency
Horton
(1932)
Depicts the texture
and relative
spacing of
drainage lines in
the basin
Texture Ratio Tr Tr = N1/P
N1 = number of first
order streams
basin
Horton
(1932)
Gives information
about underlying
geology,
infiltration
capacity of
bedrock and relief
aspects of the sub
basins
Constant of channel
maintenance
C C = 1/ Dd
where Dd = drainage
density
Schumm
(1956)
Gives information
about the basin
area, number of
square units of

12 | P a g e
river basin surface
required to sustain
one linear unit of
drainage channel
Constant of river
network development
Rz Rz = Lj / Lm
where Lj = length of
river of order j
Lm = length of final
order river
Zhou
(2006)
Gives information
about the
alterations in the
river network,
length of stream
due to
urbanization
River network
complexity
Rnc Rnc = N0 * (Lu/ Lm)
where N0 = stream
order
Lu = cumulative stream
length of all orders
Lm = length of final
order river
Zhou
(2006)
Indicative of the
structural
complexity of the
basin

13 | P a g e
Relief parameters
Morphometric
parameter
Basin Relief H H = Hmax - Hmin
where Hmax = max.
elevation
Hmin = min. elevation
Schumm
(1956)
Indicates
infiltration and
runoff
characteristics of
basin
Relief ratio R R = H/ Lb
where H = basin relief
Schumm
(1956)
Relation between
relief and gradient.
Indicates steepness
of gradient and
intensity of erosion
Relative relief Rr Rr = 100 * H/P
where H = basin relief
basin
Schumm
(1956)
Relation between
relief and
perimeter of basin.
Indicates variation
of slope with
perimeter of basin

14 | P a g e
Ruggedness number Rn Rn = Dd * H
where Dd = drainage
density
H = basin relief
Melton
(1957)
Indicates structural
complexity of the
terrain, intensity of
erosion within the
basin. Categorizes
basin as rugged and
non-rugged
Hypsometric Integral HI HI = (Emean – Emin) /
(Emax – Emin)
where Emean = Mean
elevation of the basin
Emin = Minimum
Emax = Maximum
Pike and
Wilson
(1971)
Indicates the stage
of development and
age of basin as
youth, mature and
old
Hierarchical anomaly
density
Ga Number of 1st order
streams that make the
drainage network
perfectly hierarchized
Avena et al.
(1967)
Indicates the
number of 1st order
streams required to
make the drainage
network perfectly
hierarchized

15 | P a g e
Hierarchical anomaly
index
Δa Δa = Ga/N1
where N1 = the total
number of 1st order
streams
Avena et al.
(1967)
Index of 1st order
streams in perfectly
hierarchized basin.
Denudation rate index Tu logTu = 1.47780 +
0.32619 Dd + 0.10247
Δa ( if Dd ≤ 6 )
Ciccacci et
al. (1980)
Indicates amount of
suspended
sediment yield
transported in
suspension per unit
area of the
catchment
2.1.1 Linear aspects
The linear aspect of measurement includes the following parameters:
 Stream number (Nu)
Stream number is the number of stream segments of each order. According to
Horton, the count of stream channels in its order is known as stream number. The
maximum frequency occurs in case of first order streams and decreases
subsequently as the stream order increases.
The primary ordered stream is the 1st, the confluence of two 1st order streams
yields segments of 2nd order, two 2nd order streams join to form a segment of 3rd
order and so on. When two channel of different order join then the higher order is

16 | P a g e
maintained. Generally, the trunk stream is defined as the stream segment of
highest order.
Drainage patterns are defined by the stream network. Patterns of stream network
from the basin are generally observed to be of dendritic type for 1st ordered
streams, which indicate the homogeneity in texture and lack of structural control.
 Stream order (U)
It is the hierarchical ranking of stream networks, based on hierarchic ranking
method proposed by Strahler (1964). This information is useful in relating to the
size of the contributing basin.
As the stream order increases, number and mean slope of the stream decreases in
an inverse geometric ratio. The mean stream length and mean area of drainage
basin also increases along with the discharge in a geometric ratio.
Maximum landslide incidences are recorded in areas with a high density of 1st
order streams.
 Stream length (Lu)
It is one of the most important hydrological characteristics. The length measured
from mouth of a river to the drainage divide is the stream length. This is computed
based on the law proposed by Horton (1945).
The streams of relatively smaller length are characteristics of areas with larger
slopes and finer textures. Longer lengths of streams are generally indicative of
flatter gradient.
Generally, the total length of stream segments is maximum in first order stream
and decreases as stream order increases. A change in the length indicates flowing

17 | P a g e
of streams from high altitude, lithological variation and moderately steep slopes
(Singh 1997).
The observation of stream order verifies the Horton’s law of stream number i.e.
the number of stream segment of each order forms an inverse geometric sequence
with order number. It reveals the surface runoff characteristics.
A linear plot of logarithm of stream length v/s stream order indicates the
homogenous rock pattern, neutral soil cover. A non-linear pattern indicates the
terrain is classified by variation in soil cover, lithology and topography
 Mean stream length (Lsm)
It is a characteristic property relating the drainage network components and its
associated basin surfaces (Strahler, 1964). This is calculated by dividing the total
stream length of order ‘U’ by the number of streams of segments inthat order (Nu).
Variation in the values of mean stream length is due to changes in topographic
elevation and slope of the area. The mean stream length of stream increases with
increase of the order.
 Stream length ratio (RL)
It is the ratio of the mean length of the one order stream to the next lower order of
the stream segments. The stream length ratio between the streams of different
orders show a change in each sub-basin.
This change can be attributed to the variation in the slope and topography of the
basin, indicating the late youth stage of geomorphic development in the streams
of the study area.
The stream length ratio values between streams of different order in the basin
reveal variations in slope and topography.

18 | P a g e
 Bifurcation ratio (Rb)
Schumm (1956), proposed the term bifurcation ratio, which is defined as the ratio
of the number of the stream segments of given order to the number of segments of
the next higher orders. It shows a small range of variation for different regions or
for different environments except where the powerful geological control
dominates (Strahler, 1957).
The geological and lithological development of the drainage basin bring about a
change in its value (Strahler, 1964). Higher values of Rb indicate a strong structural
control and complexity in the drainage pattern whereas lower values indicate that
the sub-basins are less affected by structural disturbances.
It is indicative of the shape of the basin such as an elongated basin is likely to have
a high value of Rb, whereas a circular basin is likely to have low value.
After studying a diverse range of drainage basins, Horton (1945) proposed that
certain ranges for the bifurcation ratio such as about 2 for ﬂat area, up to 3 for a
rolling drainage basin and has a value up to 4 for a highly dissected or
mountainous basin.
In a similar conclusion, Strahler (1964) stated that values characteristically range
between 3.0 and 5.0, for a basin in which the geological structures do not distort
the drainage pattern.
 Mean Bifurcation ratio (Rbm)
It indicates the mean value of the bifurcation ratio for all sub-basins.

19 | P a g e
 Length of overland flow (Lg)
Horton (1945) proposed, the length of overland flow as the length of the flow path
projected to the horizontal of the non-channel flow from a point on the adjacent
stream channel, and its value is approximately equal to the half of reciprocal of the
drainage density of the basin.
Alternatively, it can also be defined as the length of water over the ground before
it gets concentrated into definite stream channels. It is mostly influenced by both
hydrologic and physiographic structures of the area and is related inversely to the
average slope of streams.
A higher value is indicative of larger surface runoff from the basin whereas a lower
value suggests good amount of infiltration with less surface runoff.
2.1.2 Areal aspects
The areal aspect of measurement includes the following parameters:
 Drainage density (Dd)
It is the ratio of the total length of streams of all orders per drainage area and
indicates the closeness of the spacing of channels (Langbein 1947). Drainage
density is an important indicator of the linear characteristics of the landforms in
the stream-eroded topographical structures (Horton 1932).
It measures the relationship between precipitations and the slope gradient to
determine the runoff rate in the catchment. It is identified that the drainage
density of the sub-basin area relates to the distribution of stream segments, length
of streams, topography, relief, climate, rock types and infiltration capacity (Smith
1950).

20 | P a g e
It is well known that the amount and type of precipitation influences the quantity
and characters of surface run-off. An area with high precipitation such as
thundershowers loses greater percentage of rainfall in run-off resulting in more
surface drainage lines. Amount of vegetation and infiltration capacity of soils,
which influence the rate of surface run-offs affect the drainage texture of an area.
A low drainage density value generally results in the areas of highly resistant or
permeable subsoil material, dense vegetation and low relief. High drainage density
is the result of weak or impermeable subsurface material, sparse vegetation and
mountainous relief. A low density leads to coarse drainage texture whereas high
drainage density leads to fine drainage texture.
Observations from Chankao (1982) suggest that watersheds with adequate
drainage, have Dd > 5 and with poor drainage have Dd < 5.
High drainage density (>13.7) is indicative of impermeable subsoil thereby
leading to fine drainage texture, sparse vegetation and mountainous relief.
Low drainage density (<5) indicates highly permeable subsoil, low relief, which
leads to coarse drainage texture and thick vegetative cover.
Lower values generally tend to occur on granite, gneiss and schist regions and
areas which are highly resistant.
 Stream frequency (Fs)
Stream frequency is the total number of stream segment of all orders per unit area
(Horton 1932). Its value indicates that the origin and development of stream in
the sub-basin is mainly determined by rainfall and topographical conditions.
A low value of stream frequency of the drainage basin represents that the streams
has much fewer structural disturbances that cause a high rate of surface runoff and
fast stream ﬂow from the higher-order streams (Vincy et al. 2012). This condition

21 | P a g e
is also found in this area where a large amount of sediment has been eroded from
the weathered rocky surface and deposited in the coastal estuary.
Moreover, it is identiﬁed that the average value of drainage density and stream
frequency value are nearly close with positive correlation; this reveals that the
lengths of the streams are strongly controlled by slope and geological structures.
 Drainage texture (T)
It is the total number of stream segments of all orders per unit perimeter of the
area (Horton, 1945). It is one of the important concepts of geomorphology which
means the relative spacing of drainage lines. According to Horton (1945),
infiltration capacity is the single important factor which influences drainage
texture.
Smith (1950), defines five different drainage textures as classified, based on the
drainage density. A drainage density less than 2 indicates very coarse, between 2
and 4 is coarse, between 4 and 6 is moderate, between 6 and 8 is fine and greater
than 8 is very fine drainage texture.
 Form factor (Ff)
Horton (1932) defined the form factor as the ratio of the area of the basin to the
square of basin length i.e. distance between the point of outlet and upper limit of
sub-basin. Its value would always be greater than 0.78 for a perfectly circular basin
(Strahler, 1932).
It is an important parameter to describe the shape of the catchment area. Smaller
the value, more elongated will be the basin. Basins with high form factors
experience larger peak flows of shorter duration, whereas elongated watersheds
experience lower peak flows of longer duration.

22 | P a g e
Ff < 0.2 indicates an elongated basin, having a flatter peak flow for longer
duration.
Ff < 0.5 indicates a semi-circular basin, having a moderate peak flow for
moderate duration.
Ff = 0.7854 indicate circular basin, having a high peak flow for shorter
duration.
 Circulatory ratio (Rc)
This ratio is a factor that represents the shape characteristics of the catchment
area. The circulatory ratio is derived from the ratio of the area of sub-basin to the
area of circle having circumference equal to the perimeter of the sub-basin (Miller
1953).
It is mainly concerned with the length and frequency of streams, geological
structures, land use/land cover, climate, relief and slope of the basin. Its value
indicates that the shape of the sub-basin area is an elongated circle. The length
and frequency of streams, geological structures, land-use/land cover, climate,
relief and slope of the basin influence its value.
A value of Rc < 0.4 indicates strongly elongated and homogenous rock with high
runoff. A value equal to 1 indicates a circular shaped basin.
 Elongation ratio (Re)
It is an important parameter to analyse the shape of a sub-basin area. This is
deﬁned as the ratio between the diameter of the circle having an area equal to the
sub-basin and the maximum length of the sub-basin. The elongation ratio values
generally exhibit variation from 0.6 to 1.0 over a wide variety of climatic and
geologic types.

23 | P a g e
Values generally vary from 0.6 to 1.0 over a wide variety of climatic and geologic
types. Re values close to unity correspond typically to regions of low relief,
whereas values in the range 0.6–0.8 are usually associated with high relief and
steep ground slope (Strahler 1964).
These values can be grouped into three categories namely,
(a) Circular (>0.9),
(b) Oval (0.9-0.8),
(c) Less elongated (<0.7)
 Texture ratio (Tr)
It is estimated as the ratio between the first order streams and perimeter of the
basin. Its value depends on the underlying geology, infiltration capacity of bedrock
and relief aspects of the sub basins.
It also depends upon a number of natural factors such as climate, rainfall,
vegetation, rock and soil type and stages of development.
 Constant of channel maintenance (C)
The inverse of drainage density is termed as the constant of channel maintenance.
It indicates the number of square units of river basin surface required to sustain
one linear unit of drainage channel. A plain area requires a large surface basin area
to maintain a single unit of channel than as compared to a hilly terrain.
Higher values indicate the basin area of lower order drainages are relatively larger
than the sub-basins which have a lower value. However, a low value minimizes
length of overland ﬂow, thereby water discharges quickly as channel ﬂows under
sparse vegetation cover.

24 | P a g e
 Coefficient of River network development (Rz)
It is an indicator to quantify the alterations of the river network, and is defined as
the length of development of the rivers of order j as compared with the final order
river, which remains the most stable in the context of influences on its length and
other attributes, due to urbanization (Zhou, 2011).
 River Network complexity (Rnc)
River network complexity is used as an indicator to assess the various alterations
in the river network. Its value depicts the structural complexity of the network,
taking the length and the stream order into account (GDSB 2006).
2.1.3 Relief aspects
The relief aspect of measurement includes the following parameters:
 Basin relief (H)
Relief is the elevation difference between the highest and the lowest point in the
sub-basin. A high value indicates low infiltration, conversely a high runoff
condition.
 Relief ratio (R)
The ratio of the maximum relief to the horizontal distance, along the longest
dimension of the basin, parallel to the principal drainage line is termed as relief
ratio (Schumm, 1956). It produces a direct relationship between the relief and

25 | P a g e
channel gradient. Its value normally increases with decreasing drainage area and
size of the basin, of a given drainage basin (Gottschalk, 1964).
Relief ratio measures the overall steepness of a drainage basin and is an indicator
of the intensity of erosion process operating on slope of the basin.
 Relative relief (Rr)
Relative ratio is the ratio of the relief to the perimeter of the sub-basin.
 Ruggedness Number (Rn)
Ruggedness number is a dimensionless quantity formed of the product of basin
relief and drainage density, wherein both are in the same units.
A high value indicates the structural complexity of a terrain is highly susceptible
to erosion. The areas with high relief and low drainage density are rugged as
compared to areas with low relief and high drainage density.
Basins with high Rn (>0.5) are highly susceptible to erosion with an increased
peak discharge.
 Hypsometric Integral (HI)
This integral value is described as the ratio of the range of mean elevation and
minimum elevation (Emean–Emin) to the range of maximum and minimum
elevation (Emax–Emin) of the basin.
The value of HI (Hypsometric Integral) is denoted as the number of classes that
coarsely summarizes the relief of the basin.

26 | P a g e
 Hierarchical anomaly density (Ga)
The value of hierarchical anomaly density (Ga) is selected on the basis of the
minimum number of streams in each order (u ≤ 1) involved to make a drainage
network perfectly ordered (hierarchized) in a tree-shaped structure (Melton
1958).
 Hierarchical anomaly index (Δa)
The hierarchical anomaly index (Δa) is obtained from the ratio (Ga/N1) of
hierarchical anomaly density and the number of first-order streams actually
occurring in the drainage basin (Avena et al. 1967).
 Denudation rate index (Tu)
The denudation rate index (Tu) relates the values of drainage density and
hierarchical anomaly index, to evaluate the denudation power within the drainage
basins and the amount of suspended sediment yield (t/km2/year) transported in
suspension per unit area of the catchment.

27 | P a g e
3. Case Study
An extensive and detailed analysis accounting for the various morphometric
parameters under linear, areal and relief aspects of measurements was performed.
The test site is located along the foothills of the Western Ghats, near the city of
Pune and comprises of three large scale basins. The three rivers viz. Ghod, Bhima
and Mula-Mutha, which are amongst the largest in the state, broadly consist of 23
sub-basins of Ghod, 22 of Bhima and 11 of Mula-Mutha. The Ghod basin has the
largest areal extent with an area of 4460.06 sq.km followed by the Bhima basin
with 3809.67 sq.km and the Mula-Mutha basin with 2920.47 sq.km.

28 | P a g e
Figure 2. Study area location of Bhima, Ghod and Mula-Mutha basins.

29 | P a g e
Figure 3. Morphometric Analysis map

30 | P a g e
In order to understand the influences of geomorphology and drainage basin
morphometry on the hydrological patterns prevailing in the area, the drainage
streams of each of the sub-basins were digitized in ArcGIS 10.1, and the slope and
DEM thematic layers were produced. Primary measurements such as stream
number, stream-length, sub-basin area, sub-basin width, sub-basin elongated
length, sub-basin perimeter and total relief were derived from the thematic layers.
The mean value of the derived parameters for all three basins are presented in the
following table.

31 | P a g e
Table 1. Mean values of derived parameters of the three basins.
Parameters GHOD basin BHIMA basin MULA-MUTHA basin
Cumulative stream length 559.5239 449.0268 697.9669
Stream length ratio 2.6797 11.8498 13.5888
Mean Bifurcation ratio 4.2919 3.9583 4.0563
Length of overland flow 0.1839 km 0.2334 km 19.8897 km
Drainage texture 11.4007 8.7819 19.8897
Texture ratio 4.9592 4.1109 7.8331
Form factor 0.1956 0.1958 0.2261
Elongation ratio 0.4879 0.4866 0.5277
Circulatory ratio 0.2161 0.1999 0.2543
Relief ratio 12.8245 11.1589 20.8335
Relative relief 400.0599 345.9838 661.1974
Drainage density 2.7936 km-1 2.3816 km-1 3.3221 km-1
Ruggedness No 1096.2110 931.1506 1907.237
Constant of channel
maintenance
0.3678 0.4669 0.3248
Hypsometric Integral 0.2901 0.3176 0.2344
Coefficient of River
Network Development
896.2762 1045.2082 2691.442
River Network Complexity 28376.3501 35844.9136 110617
Hierarchical Anomaly
Density
268.2609 224.6363 367.0769
Hierarchical Anomaly
Index
0.4336 0.4547 0.4292
Denundation Rate Index 268.7398 216.5031 457.2164

32 | P a g e
4. Results & Discussion
4.1 Estimating dominant parameters
Morphometry by and large affects the hydrological processes rather indirectly
through their dependency on several other factors such as soil, geology, vegetation
cover and climate (Schmidt et al. 2000). The interrelationship between
morphometric parameters varies from basin to basin under diverse topography
and climatic condition. Understanding these relationship would enable the
identification of the dominant parameters acting on a particular basin.
Assuming other factors acting uniformly, the interrelationship among
morphometric parameters for the three basins are inspected for correlation, and
the highest correlating parameters are obtained and selected to be dominant
acting over the basin. The correlation matrices for the three basins are shown

33 | P a g e
Figure4.CorrelationmatrixofmorphometricvariablesforGHODbasin.

34 | P a g e
Figure5.CorrelationmatrixofmorphometricvariablesforBHIMAbasin.

35 | P a g e
Figure6.CorrelationmatrixofmorphometricvariablesforMULA-MUTHAbasin

36 | P a g e
Salient observations from the correlation matrices are:
 Drainage density is positively correlated with drainage texture, basin relief,
ruggedness number, hypsometric integral, denudation rate index and
bifurcation ratio. It is negatively correlated with length of overland flow,
form factor, elongation ratio, constant of channel maintenance and
hierarchical anomaly index.
 Drainage texture is positively correlated with circulatory ratio, basin relief,
ruggedness number, hypsometric integral, denudation rate index,
bifurcation ratio and drainage density. It is negatively correlated with form
factor, elongation ratio and constant of channel maintenance, hierarchical
anomaly density and hierarchical anomaly index.
 Significant negative relation is seen between Ruggedness number and
length of overland flow, form factor, elongation ratio and hierarchical
anomaly density.
 Similarly, length of overland flow is negatively related with drainage
texture, basin relief, ruggedness number, hypsometric integral, denudation
rate index and drainage density. It is evident that a large number of
morphometric parameters are influencing the length of overland flow in the
study basins.
 The constant of channel maintenance is largely positively correlated with
the length of overland flow, form factor and elongation ratio, whereas a
strong negative correlation exists with drainage texture, ruggedness
number, denudation rate index and drainage density.
It is evident from above results that the drainage density, drainage texture,
ruggedness number, length of overland flow and the constant of channel
maintenance are significantly correlated with other morphometric parameters,
and can thus be selected as dominant parameters over the basins. These

37 | P a g e
parameters are indicative of almost all aspects of the basin shape, size,
hydrological conditions, drainage pattern, surface runoff and infiltration capacity.
4.2 Further application
The morphometric parameters are considered as criteria and play a major role in
the decision-making for basin prioritization and characterization. Satty (1980)
defines that the decision criteria requires to be non-redundant and independent.
The independent decision criteria can be obtained from the correlation matrices
computed above. It is evident from above results that the drainage density,
drainage texture, ruggedness number, length of overland flow and the constant of
channel maintenance are significantly correlated with other morphometric
parameters, and can thus be selected as dominant parameters over the basins. The
parameters are selected in such a way that maximum number of independent
criteria can be taken into consideration.

38 | P a g e
References
Avena GC, Giuliano G, Palmieri EL (1967); Quantitative evaluation of the hierarchization
and evolution of drainage networks. Bull Soc Geol Italy 86:781–796.
Bahrami S (2013); Tectonic controls on the morphometry of alluvial fans around
Danehkhoshk anticline, Zagros. Iran Geomorphol 180 & 181:217–230.
Ciccacci S, Del Monte M, Marini R (2003); Denudational processes and recent
morphological change in a sample area of the Orcia River upper basin (Southern
Tuscany). Geogr Fis Dinam Quat 26:97–109.
Chankao, K. (1982). Principle of Watershed Management. Bangkok, Thailand: Faculty of
Forestry, Kasetsart University.
Della Seta M, Del Monte M, Fredi P, Palmieri EL (2007); Direct and indirect evaluation of
denudation rates in Central Italy. Catena 71:21–30.
Gottschalk, L.C. (1964);Reservoir sedimentation. In. V.T.Chow (ed), Handbook of Applied
Geology. McGraw Hill Book Company, New York, Section 7-1.
Horton RE. 1932. Drainage-basin characteristics. Trans Am Geophys Union. 13350-
361
Horton RE. 1945. Erosional development of streams and their drainage basins;
hydrophysical approach to quantitative morphology. Bull Geol Soc Am. 56:275–
370.
Jain PK. 2009. Groundwater Information of Pune district, Maharashtra. Technical report
1612/ DBR/2009, Central Ground Water Board (CGWB), Nagpur, India.

39 | P a g e
Kaliraj • N. Chandrasekar • N. S. Magesh; Morphometric analysis of the River
Thamirabarani sub-basin in Kanyakumari District, South west coast of Tamil
Nadu, India, using remote sensing and GIS; S. Environ Earth Sci DOI
10.1007/s12665-014-3914-1.
Magesh N, Chandrasekar N, Soundranayagam J. 2011. Morphometric evaluation of
Papanasam and Manimuthar watersheds, parts of Western Ghats, Tirunelveli
district, Tamil Nadu, India: a GIS approach. Environ Earth Sci. 64:373–381.
Melton MA (1958); Geometric properties of mature drainage systems and their
representation in E4 Phase Space. J Geol 66:35–54
Miller VC (1953); A quantitative geomorphologic study of drainage basin
characteristics in the Clinch Mountain area, Virginia and Tennessee, Project NR
389042, Technical Report 3. Columbia University Department of Geology, ONR
Geography Branch New York.
Nag S, Chakraborty S. 2003. Influence of rock types and structures in the development of
drainage network in hard rock area. J Indian Soc Remote Sens. 31:25–35.
National Institute of Hydrology (1993); Geomorphological characteristics of Narmada
basin up to Manot. CS (AR)—128, NIH, Roorkee, Technical report, pp 1–34.
Pike RJ, Wilson SE (1971); Elevation-relief ratio hypsometric integral and geomorphic
area-altitude analysis. Geol Soc Am Bull 82:1079–1084
Satty TL. 1980. The analytic hierarchy process; New York, NY: McGraw-Hill.
Strahler AN. 1964. Handbook of applied hydrology. In: Chow VT, editor. Quantitative
geomorphologyofdrainagebasinsandchannelnetworks. New York, NY: Mc-Graw
Hill Book Company; p. 39–76.

40 | P a g e
Strahler AN. 1957. Quantitative analysis of watershed geomorphology. Trans Am
Geophys Union. 38:913–920.
Schmidt J, Hennrich K, Dikau R. 2000. Scales and similarities in runoff processes with
respect to geomorphometry. Hydrol Process. 14:1963–1979.
Schumm SA. 1956. Evolution ofdrainagesystems and slopesin bad landsat Perth Amboy,
New Jersey. Bull Geol Soc Am. 67:597–646.
Smith KG (1950); Standards for grading textures of erosional topography. Am J Sci
248:655–668
Zhou; Peijun Shi; Jing’ai Wang; Deyong Yu & Lu Gao, Rapid Urbanization and Implications
for River Ecological Services Restoration: Case Study in Shenzhen, China Hongjian
2011 American Society of Civil Engineers.
Usha Chirala, Nooka Ratnam Kinthada, Murali Krishna Gurram; GEOMORPHOMETRIC
PARAMETERS FOR THE HYDROLOGICAL CHARACTERIZATION OF MEGHADRIGEDDA
WATERSHED, VISAKHAPATNAM, INDIA – A GIS APPROACH, Vol. 4 No.07 July 2012,
International Journal of Engineering Science and Technology (IJEST)

Remote Sensing & GIS based drainage morphometry

More Related Content

What's hot

Similar to Remote Sensing & GIS based drainage morphometry

Recently uploaded

Remote Sensing & GIS based drainage morphometry