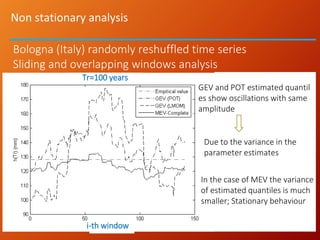
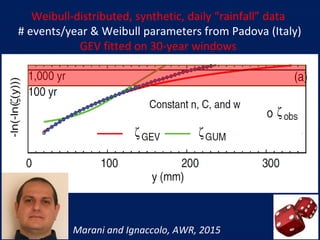
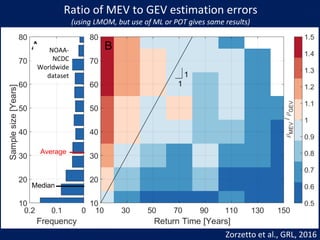
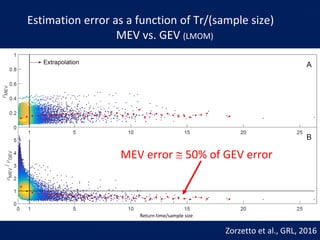
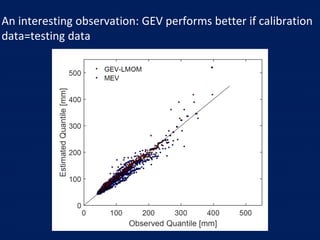
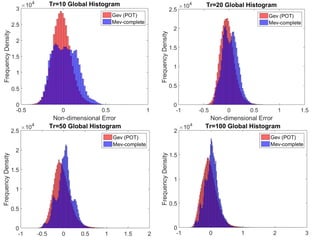
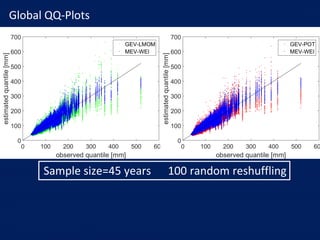
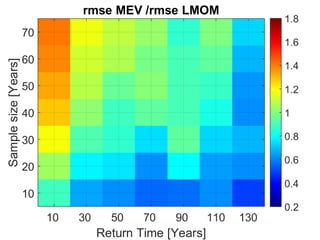
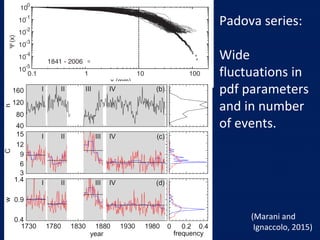
- The document presents the Metastatistical Extreme Value (MEV) distribution as an improvement over classical extreme value theory. - MEV accounts for the stochasticity in both the number of rainfall events per year and the parameters of the underlying rainfall distribution. This better represents scenarios with limited data where the asymptotic assumptions of classical methods break down. - The author applies MEV using a Weibull distribution for daily rainfall and finds it outperforms generalized extreme value and peak over threshold methods by reducing estimation errors of rainfall quantiles by around 50% on average across diverse datasets.

1. XXXV CONVEGNO NAZIONALE DI IDRAULICA
E COSTRUZIONI IDRAULICHE
Bologna, 14-16 Settembre 2016
The Metastatistical Extreme Value
Distribution
Metodi Statistici per le Applicazioni Idrologiche
Enrico Zorzetto1, Gianluca Botter2,
Marco Marani1,2,*
1Earth and Ocean Science Division, Duke University
2 DICEA, Universita’ di Padova
* marco.marani@unipd.it

2. Classical Extreme Value Theory (EVT)
[Fischer-Tippett-Gnedenko, 1928-1943]
Block Maxima:
Three-Type Theorem:
- As n  ∞
-After renormalization, 3 possible
asymptotic distributions,
summarized by GEV (e.g. Von Mises, 1936):
= Maxima n-event blocks
h[mm]
𝑥 𝑛
1937 19381936 1939 194019411942
𝑥 𝑛 = max
𝑛
(𝑥𝑖)
for i.i.d 𝑥𝑖 ∶ 𝐻 𝑛 𝑥 = 𝐹 𝑥 𝑛
𝐻 𝑥 = exp − 1 +
𝜉
𝜓
𝑥 − 𝜇
+
−
1
𝜉

3. Marani and Ignaccolo, AWR, 2015
Weibull-distributed, synthetic, daily “rainfall” data
# events/year & Weibull parameters from Padova (Italy)
GEV fitted on 30-year windows

4. Considerations on the validity of the classical EVT
- Incomplete convergence to limiting distribution: n <<  !!!
(e.g. Koutsoyiannis, 2013; Serinaldi and Kilsby, 2014).
- When number of events is small yearly maxima also come from bulk of
distribution, not just the tail (we are far from a limiting form)
- GEV - Maximum Likelihood only uses yearly maxima and neglects most
of the data.
- Peak Over Threshold uses more data, but still a fraction of available
information.

5. A Metastatistical Extreme Value distribution (MEV)
𝐻 𝑛 𝑥 = 𝐹 𝑥; Ԧ𝜃
𝑛
for i.i.d. 𝑋𝑖
′
𝑠.
F(X; ) = cdf of “ordinary events”
The Block-maxima distribution
Expected block-maxima distribution compounding stochastic
n and :
Marani and Ignaccolo, AWR, 2015; Zorzetto et al., GRL, 2016
G(n,𝜃) = joint prob distrib. of the
parameters.
Approximating expectations with sample averages….
Parameters of
ordinary distributions

6. A Metastatistical Extreme Value distribution (MEV)
Marani and Ignaccolo, AWR 2015; Zorzetto et al., GRL 2016
 𝑥 ≅
1
𝑇
෍
𝑗=1
𝑇
𝐹(𝑥; 𝜃𝑗) 𝑛 𝑗
T = # years over which n
and 𝜃 are estimated
… approximating expectations with sample averages:
MEV:

7. MEV distribution – conceptual interpretation
Zorzetto et al., GRL 2016

8. A choice for F(x) - the pdf of daily «ordinary» rainfall
𝑅 𝑎𝑐𝑐 = ത𝑘ത𝑞𝑚
𝐹 𝑥 = 1 − 𝑒
𝑥
𝐶
𝑤 Weibull Parent
distribution
ത𝑘=precipitation efficiency
ത𝑞=specific humidity
m=advection mass
[Wilson e Tuomi, 2005]
-Simple two-layers atmospheric model
-Temporal average

9. MEV-Weibull distribution
Marani and Ignaccolo, AWR, 2015; Zorzetto et al., GRL, 2016
The MEV expression:
 𝑥 ≅
1
𝑇
෍
𝑗=1
𝑇
𝐹(𝑥; 𝜃𝑗) 𝑛 𝑗 T = # sub-periods over which n
and 𝜃 are estimated
In the Weibull case becomes:
 𝑥 ≅
1
𝑇
෍
𝑗=1
𝑇
1 − 𝑒
𝑥
𝐶 𝑗
𝑤 𝑗 𝑛 𝑗

10. Marani and Ignaccolo, AWR, 2015
Weibull-distributed synthetic data
GEV and MEV fitted on 30-year windows
n random, c and w constant
n, C, and w are constant
n constant, C and w random

11. How about reality?
36 daily rainfall timeseries, 106 -275 years of daily observations,
( <L> =135 yrs) Less than 5% of missing data
OXFORD
SHEFFIELD
HOOFDOORP
PUTTEN
ZURICH
HEERDE
S. BERNARD
MELBOURNE
MILANO
PADOVA
BOLOGNA
CAPE TOWN
SAN FRANCISCO
ROOSVELT
ASHEVILLE
PHILADEPHIA
KINGSTON
ALBANY
DUBLIN
ZAGREB
WORCESTER
DUBLIN
SYDNEY

12. Method of analysis
• To eliminate correlation and non-stationarity
• Preserving the true (unknown) distribution of the
parameters and numbers of wet days.
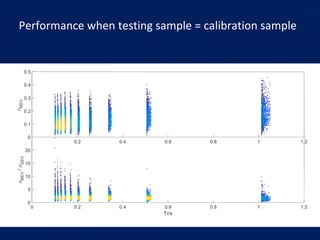
• Fit on a sample of size s
• Test on remaining data. Non dimensional Root
Mean Square Error:
Which is studied as a function of sample size s.
Bootstrap - Reshuffling of daily data preserving
(1) yearly number of events, and
(2) observed values (i.e. Pdf’s)
ORIGINAL TIME SERIES
𝜖 =
1
𝑁
෍ (
ො𝑥 − 𝑥 𝑜𝑏𝑠
𝑥 𝑜𝑏𝑠
)2
RANDOMLY RESHUFFLED TIME SERIES
T Years
h [mm]
h [mm]
t [days]
t [days]

13. Ratio of MEV to GEV estimation errors
(using LMOM, but use of ML or POT gives same results)
NOAA-
NCDC
Worldwide
dataset
Zorzetto et al., GRL, 2016

14. Estimation error as a function of Tr/(sample size)
MEV vs. GEV (LMOM)
Zorzetto et al., GRL, 2016
Return time/sample size
MEV error  50% of GEV error

15. Conclusions
MEV ouperforms classical EV distributions:
- Reliable assessment of high quantiles and small
samples (50% improvement over GEV)
- Better use of the available daily data
- Removal of the asymptotic hypothesis
Future:
1.MEV is general approach (floods, wind, storm sur
ges ...)
2. MEV is arguably suited to tackle non-stationarity

16. Grazie per l’attenzione

17. Some thoughts on non stationarity
Bologna (Italy) original 180 years time-series
Sliding and overlapping windows analysis
GEV and POT estimated q
uantile shows higher vari
ance
MEV shows a positive
trend in est. quantiles
Due to trends in parameter
s of Weibull distribution
Tr=100 years
i-th temporal window

18. An interesting observation: GEV performs better if calibration
data=testing data

19. Tr=100 daily rainfall from TRMM observations (17 yrs)

20. Estimation error as a function of Tr/(sample size)

21. Distribution of the error computed over 1000 random reshuffling, for
all the analyzed datasets.
Quantiles (Tr=100 yrs) estimated by GEV, POT, MEV
calibrated over 30-years samples
Error distribution
𝜖 =
ො𝑥 − 𝑥 𝑜𝑏𝑠
𝑥 𝑜𝑏𝑠
ො𝑥 = 𝐹−1
1 −
1
𝑇𝑟𝑖
𝑥 𝑜𝑏𝑠 from the observational
(independent) sample

22. Distribution of the error computed over 1000 random generation
s, for all the analyzed datasets.
Theoretical quantiles (Tr=100 yrs) estimated by GEV, POT, MEV c
alibrated over 30-years samples
Error distribution
𝜖 =
ො𝑥 − 𝑥 𝑜𝑏𝑠
𝑥 𝑜𝑏𝑠
ො𝑥 = 𝐹−1
1 −
1
𝑇𝑟𝑖
𝑥 𝑜𝑏𝑠 from the observational
(independent) sample

23. Global QQ-Plots
Sample size=45 years 100 random reshuffling

24. Global QQ plots
GEV/ POT are a good fit for the calibration sa
mple but they fail in describing the stochasti
c process from which the sample has been g
enerated
MEV allows a better description of the under
lying process; less variance in high quantile e
stimation
ൗ𝑃. 𝑡𝑖
𝑚𝑚2

25. The MEV domain

26. N
1982 1986198519841983
t
h [mm]
𝑛1 = 97 𝑛2 = 105 𝑛3 = 89 𝑛4 = 94 𝑛5 = 114
𝐶1, 𝑤1 𝐶2, 𝑤2 𝐶3, 𝑤3 𝐶4, 𝑤4 𝐶5, 𝑤5
2. Fit Weibull to the singl𝑒 𝑦𝑒𝑎𝑟𝑠 𝐶𝑖, 𝑤𝑖
1. Sampling n from the distribution p(n|C,w)
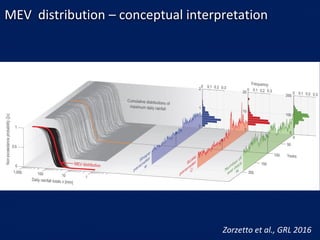
The MEV distribution
𝐹 𝑥 = 1 − 𝑒
𝑥
𝐶
𝑤
• Assuming Weibull as a pdf for daily rainfall
• Fit performed using Probability Weighted Moments (Greenwood et al, 1979)
Number of
events/ year

27. 𝜁 𝑥 = ෍
𝑛=1
∞
ඵ
𝐶 𝑤
𝑔 𝑛, 𝐶, 𝑤 1 − 𝑒
𝑥
𝐶
𝑤 𝑛
𝑑𝐶𝑑𝑤
• Weibull parameters 𝜃 = 𝐶, 𝑤 and 𝑁 are random variables themselves
• The CDF of annual maximum is the mean on all their possible realizations
The Metastatistical Extreme Value Distribution
n
𝑓(𝑛)
𝑓(𝑤)
𝑓(𝐶)
Density frequencies

28. Non stationary analysis
GEV and POT estimated quantil
es show oscillations with same
amplitude
Due to the variance in the
parameter estimates
In the case of MEV the variance
of estimated quantiles is much
smaller; Stationary behaviour
Tr=100 years
i-th window
Bologna (Italy) randomly reshuffled time series
Sliding and overlapping windows analysis

29. Daily rainfall observations in Padova 1725-2015
The Padova observatory

30. (Marani and Zanetti, 2015)
The Padova daily precipitation time series 1725-2006

31. (Marani and
Ignaccolo, 2015)
Padova series:
Wide
fluctuations in
pdf parameters
and in number
of events.

32. Peak Over Threshold Method (POT)
[Balkema, De Haan & Pickand, 1975; Davison and Smith, 1990]
• Exceedances arrivals Poisson
• Distribution of excesses Generalized Pareto
Advantages:
1. Better description of the ‘tail’
2. Consistent with GEV
𝑃 𝑌 𝑚𝑎𝑥 < x = ෍
𝑛=1
∞
𝑝 𝑛 ⋅ 𝐹 𝑥 𝑛
= ෍
𝑛=1
∞
𝜆 𝑛
𝑒−𝑛
𝑛!
∙ 1 − 1 +
𝜉
𝜓
∙ 𝑥 − 𝑞
−1/𝜉
𝑛
For a fixed threshold q → Exceedances 𝑌𝑖 = 𝐻𝑖 − 𝑞 𝑖. 𝑖. 𝑑. 𝑟. 𝑣.
𝑦𝑖 = ℎ𝑖 − 𝑞

33. Performance when testing sample = calibration sample

34. Ratio of MEV estimation error to GEV-POT error