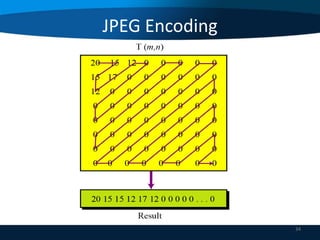
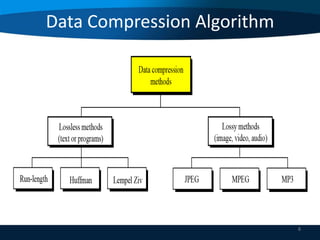
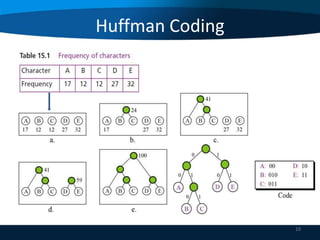
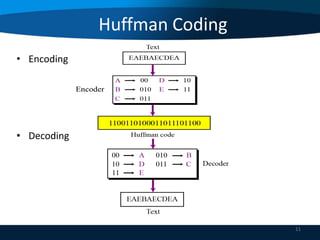
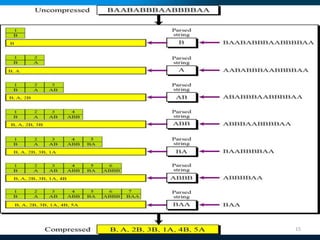
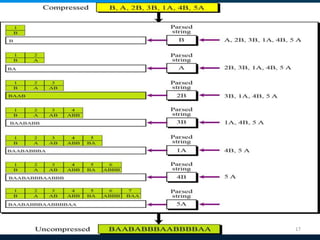
This document provides an overview of data compression techniques. It discusses lossless compression algorithms like Huffman encoding and LZW encoding which allow for exact reconstruction of the original data. It also discusses lossy compression techniques like JPEG and MPEG which allow for approximate reconstruction for images and video in order to achieve higher compression rates. JPEG divides images into 8x8 blocks and applies discrete cosine transform, quantization, and run length encoding. MPEG spatially compresses each video frame using JPEG and temporally compresses frames by removing redundant frames.

1. Data Compression
Presented to: Prof. Dr. Maha Sharkas
presented by: Sherif Mohamed
1

2. Data Compression
Outline
1)
2)
3)
4)
5)
6)
Introduction.
Types of Data Compression.
Lossless Compression.
Lossless Algorithms.
Lossy Compression.
Lossy Algorithms .
2

3. Data Compression
• It is the process of reducing the amount of
data required to represent a given quantity of
information.
• Save time and help to optimize resources
i. In sending data over communication line:
less time to transmit and less storage to
host.
• Reduce length of data transmission time over
the network.
3

4. Types of Data Compression
1. Lossless Compression.
2. Lossy Compression.
4

5. Data Compression Algorithm
• Lossless Compression
If the compressed data is reconstructed and
the original data is obtain without any loss of
information then this technique is called
lossless compression.
5

6. Types of Data Compression
• Lossy Compression
If the compressed data is reconstructed and
the approximation of original data is obtain
and loss of information occurs then this
technique is called lossy compression.
The original message can never be recovered
exactly as it was before it was compressed.
6

7. Types of Data Compression
Lossless
Original Data
Compressed
Data
Original Data
Approximated
7

8. Data Compression Algorithm
8

9. Lossless Algorithm
• Huffman Encoding
 There’s no unique Huffman code.
 Algorithm:
①
②
③
Make a leaf node for each code symbol
Add the generation probability of each symbol to the leaf node
Take the two leaf nodes with the smallest probability and connect them into
a new node
Add 1 or 0 to each of the two branches
The probability of the new node is the sum of the probabilities of the
two connecting nodes
If there is only one node left, the code construction is completed. If not, go
back to (2)
9

10. Huffman Coding
• z
10

11. Huffman Coding
• Encoding
• Decoding
11

12. Lossless Algorithm
• Lempel Ziv Walsh (LZW) Encoding
• It is dictionary based encoding
• Basic idea:
 Create a dictionary or a code table of strings used during
communication.
 If both sender and receiver have a copy of the dictionary, then
previously-encountered strings can be substituted by their index
in the dictionary.
• LZW to compress text, executable code and similar
data files to about one half their original size.
12

13. LZW Coding
 Have 2 phases:
 Building an indexed dictionary
 Compressing a string of symbols
• Algorithm:
 Extract the smallest substring that cannot be found in the
remaining uncompressed string.
 Store that substring in the dictionary as a new entry and
assign it an index value
 Substring is replaced with the index found in the dictionary
 Insert the index and the last character of the substring into
the compressed string
13

14. LZW Coding
• Lempel Ziv Compression
14

15. 15

16. LZW Coding
• Lempel Ziv Decompression
16

17. 17

18. Lossless Algorithm
• Run Length Encoding
• Simplest method of compression.
• Replace consecutive repeating occurrences of
a symbol by 1 occurrence of the symbol itself,
then followed by the number of occurrences.
18

19. Run Length Coding
• The method can be more efficient if the data
uses only 2 symbols (0s and 1s) in bit patterns
and 1 symbol is more frequent than another.
19

20. Lossy Algorithm
• Used for compressing images and video files (our
eyes cannot distinguish subtle changes, so lossy data
is acceptable).
• These methods are cheaper, less time and space.
• Several methods:
 JPEG: compress pictures and graphics
 MPEG: compress video
 MP3: compress audio
20

21. Lossy Algorithm
• JPEG Encoding
• Used to compress pictures and graphics.
• In JPEG, a grayscale picture is divided into 8x8
pixel blocks to decrease the number of calculations.
• Basic idea:
 Change the picture into a linear (vector) sets of numbers that
reveals the redundancies.
 The redundancies is then removed by one of lossless
21

22. JPEG Encoding
22

23. JPEG Encoding
• DCT(Discrete Cosine Transform)
• Image is divided into blocks of 8*8 pixels.
• For grey-scale images, pixel is represented by 8-bits.
• For color images, pixel is represented by 24-bits or
three 8-bit groups.
23

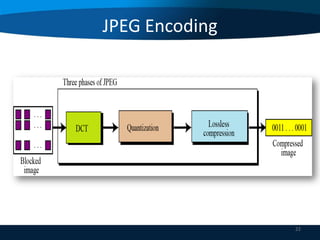
24. JPEG Encoding
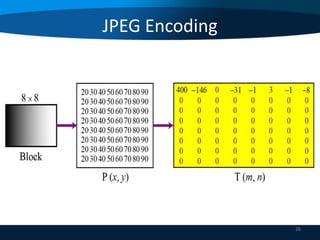
• DCT takes an 8*8 matrix and produces another 8*8
matrix and its values represent by this equation:
T[i][j] = 0.25 C(i) C(j) ∑ ∑ P[x][y] Cos(2x+1)iπ/16
* Cos (2y+1)jπ/16
 i = 0, 1, …7, j = 0, 1, …7
 C(i) = 1/√2, i =0
= 1 otherwise
T contains values called ‘Spatial frequencies’
24

25. JPEG Encoding
• T[0][0] is called the DC coefficient, related to
average values in the array, Cos 0 = 1
• Other values of T are called AC coefficients, cosine
functions of higher frequencies
 Case 1: all P’s are same, image of single color with no variation
at all, AC coefficients are all zeros.
 Case 2: little variation in P’s, many, not all, AC coefficients are
zeros.
 Case 3: large variation in P’s, a few AC coefficients are zeros.
25

26. JPEG Encoding
26

27. JPEG Encoding
P-matrix
T-matrix
• 20 30 40 50 60 …
720 -182 0 -19 0 …
30 40 50 60 70
-182 0 0 0 0
40 50 60 70 80
0
0 0 0 0
50 60 70 80 90
-19 0 0 0 0
60 70 80 90 100
0
0 0 0 0
…
…
‘Uniform color change and little fine detail, easier to
compress after DCT’
27

28. JPEG Encoding
P-matrix
T-matrix
• 100 150 50 100 100 …
835 15 -17 59 5…
200 10 110 20 200
46 -60 -36 11 14
10 200 130 30 200
-32 -9 130 105 -37
100 10 90 190 120
59 -3 27 -12 30
10 200 200 120 90
50 -71 -24 -56 -40
….
….
‘Large color change, difficult to compress after DCT’
28

29. JPEG Encoding
• Quantization
• Provides an way of ignoring small differences in an
image that may not be perceptible.
• Another array Q is obtained by dividing each
element of T by some number and rounding-off to
nearest integer ( The loss is occur in this step)
29

30. JPEG Encoding
T-matrix
Q-matrix
• 152 0 -48 0 -8…
15 0 -5 0 -1…
0 0 0 0 0
0 0 0 0 0
-48 0 38 0 -3
-5 0 4 0 0
0 0 0 0 0
0 0 0 0 0
-8 0 -3 0 13
-1 0 0 0 1
…
…
‘Divide by 10 and round-off ’
.
30

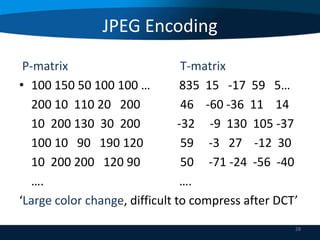
31. JPEG Encoding
• Dividing T-elements by the same number is not
practical, may result in too much loss.
• Retain the effects of lower frequencies as much as
possible.
• To define a quantization array Q, then
Q[i][j] = Round (T[i][j] ÷ U[i][j]),
i = 0, 1,.........7, j = 0, 1, …7
31

32. JPEG Encoding
• U = 1 3 5 7 9… Q= 152 0 -10 0 -1 …
3 5 7 9 11
0 0 0 0 0
5 7 9 11 13
-10 0 4 0 0
7 9 11 13 15
0 0 0 0 0
9 11 13 15 17
-1 0 0 0 0
…
…
‘Q can be well compressed due to redundant
elements’
32

33. JPEG Encoding
• Compression
 Quantized values are read from the matrix and redundant
0s are removed.
 To cluster the 0s together, the matrix is read diagonally
in an zigzag fashion. The reason is if the matrix doesn’t
have fine changes, the bottom right corner of the matrix
is all 0s.
 JPEG usually uses lossless run-length encoding at the
compression phase.
33

34. JPEG Encoding
34

35. JPEG Encoding
8x8
pixel
block
Discrete
Cosine
Transform
Quantization
Run Length,
Huffman
Encoding
to .jpg file
35

36. MPEG Encoding
Used to compress video.
 Basic idea:

 Each video is a rapid sequence of a set of frames. Each
frame is a spatial combination of pixels, or a picture.
 Compressing video =
spatially compressing each frame
+
temporally compressing a set of frames.
36

37. MPEG Encoding
• Spatial Compression
 Each frame is spatially compressed by JPEG.
• Temporal Compression
 Redundant frames are removed.
 Usually little difference from one to the next frame
is suitable for compression.
{For example, in a static scene in which someone is
talking, most frames are the same except for the
segment around the speaker’s lips, which changes
from one frame to the next}.
 Three frames: I, P, B.
37

38. MPEG Encoding
• I (intra-picture) frame: Just a JPEG encoded
image.
• P (predicted) frame: Encoded by computing
the differences between a current and a
previous frame.
• B (bidirectional) frame: Similar to P-frame
except that it is interpolated between previous
and future frame.
38

39. MPEG Encoding
• order in which to transmit: I – P – I
P is sandwiched between groups of B
P is the difference from the previous I-frame
B is interpolated from the nearest I and P
order in which to display I – B – B – P – B – B – I
39

40. Thank You
40